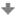Derivace

$\begin{align} \end{align}$

Globální extrémy

Tato část navazuje na podkapitolu Lokální extrémy tabulkovou metodou. Naučíte se zde nalézat globální extrémy různých funkcí. Předpokladem pro pochopení této látky je zvládnutí příkladů a úloh z podkapitoly Lokální extrémy tabulkovou metodou. Budeme hledat globální extrémy vždy jen na jednom intervalu spojitosti. Opět platí předpoklady uvedené v podkapitole Předpoklady.

Nejprve je uvedena teorie a pak příklady a úlohy.

Teoretická část

Definice

Funkce $f$ má na intervalu $I$ v bodě $x_0$ globální maximum, jestliže pro všechna $x \in I$ platí: $f(x) \leq f(x_0)$ .

Funkce $f$ má na intervalu $I$ v bodě $x_0$ globální minimum, jestliže pro všechna $x \in I$ platí: $f(x) \geq f(x_0)$ .

Globální maxima a minima nazýváme souhrnně globální extrémy.

Věta

Je-li funkce $f$ spojitá na uzavřeném intervalu, pak tam má globální maximum i minimum.

Poznámky k předchozí větě

Je-li funkce spojitá na otevřeném intervalu, nemusí tam mít žádné extrémy.

Ilustrace: Na intervalu $(0,1)$ nemá funkce $f: y = x$ žádný lokální ani globální extrém.

Je-li funkce spojitá na polouzavřeném intervalu, pak za Předpokladu 3 z podkapitoly Předpoklady platí, že tam má vždy alespoň jeden globální extrém. Z důvodu složitosti však nebudeme toto tvrzení dokazovat.

Pokud bychom o funkci spojité na polouzavřeném intervalu nic nepředpokládali, pak na takovém intervalu nemusí mít žádné globální extrémy.

Ilustrace:	Na intervalu $\langle 0,1 )$ nemá funkce $f: y = x \sin\dfrac{1}{1-x}$ žádný globální extrém.
	Funkce podobného typu je zobrazena na následujícím obrázku:

ilustrace

Věta

Je-li funkce $f$ spojitá na uzavřeném intervalu, pak jejím globálním maximem je maximum ze všech lokálních maxim a jejím globálním minimem je minimum ze všech lokálních minim.

Věta

Jestliže u funkce spojité na otevřeném nebo polouzavřeném intervalu neexistuje lokální maximum, pak tam neexistuje ani globální maximum. Podobně neexistence lokálního minima znamená neexistenci globálního minima.

Poznámka k předchozí větě

Předchozí věta vyplývá ze skutečnosti, že každý globální extrém je i lokálním extrémem.

Připomínám, že o zkoumaných funkcích předpokládáme, že na zkoumaném intervalu spojitosti je nulový nebo malý konečný počet stacionárních bodů a bodů, v nichž není derivace definována.

Za výše uvedeného předpokladu platí následující tři věty:

Věta

Každý lokální extrém je ostrým lokálním extrémem.

Věta

Je-li funkce $f$ spojitá na polouzavřeném intervalu $(a,b\rangle$ , pak existuje $\large\lim\limits_{x \to a+}\normalsize f(x)$ .

Je-li funkce $f$ spojitá na polouzavřeném intervalu $\langle a,b)$ , pak existuje $\large\lim\limits_{x \to b-}\normalsize f(x)$ .

Je-li funkce $f$ spojitá na otevřeném intervalu $(a,b)$ , pak existují obě předchozí limity.

Věta

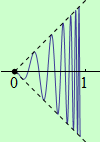
a) Nechť funkce $f$ je spojitá na polouzavřeném intervalu $(a,b\rangle$ a má alespoň jedno lokální maximum. Na daném intervalu neexistuje globální maximum, jestliže je maximum ze všech lokálních maxim nižší, než $\large\lim\limits_{x \to a+}\normalsize f(x)$ , viz následující obrázek:

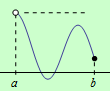
ilustrace bodu a

b) Nechť funkce $f$ je spojitá na polouzavřeném intervalu $(a,b\rangle$ a má alespoň jedno lokální minimum. Na daném intervalu neexistuje globální minimum, jestliže je minimum ze všech lokálních minim vyšší, než $\large\lim\limits_{x \to a+}\normalsize f(x)$ , viz následující obrázek:

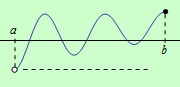
ilustrace bodu b

c) Obdobná tvrzení platí, je-li funkce $f$ spojitá na polouzavřeném intervalu $\langle a,b)$ .

d) Nechť funkce $f$ je spojitá na otevřeném intervalu $(a,b)$ a má alespoň jedno lokální maximum. Na daném intervalu neexistuje globální maximum, jestliže je maximum ze všech lokálních maxim nižší, než $\large\lim\limits_{x \to a+}\normalsize f(x)$ nebo $\large\lim\limits_{x \to b-}\normalsize f(x)$ , viz následující obrázek:

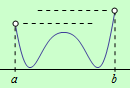
ilustrace bodu d

e) Nechť funkce $f$ je spojitá na otevřeném intervalu $(a,b)$ a má alespoň jedno lokální minimum. Na daném intervalu neexistuje globální minimum, jestliže je minimum ze všech lokálních minim vyšší, než $\large\lim\limits_{x \to a+}\normalsize f(x)$ nebo $\large\lim\limits_{x \to b-}\normalsize f(x)$ , viz následující obrázek:

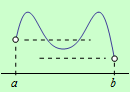
ilustrace bodu e

Příklady a úlohy

Pro hledání globálních extrémů na daném intervalu spojitosti je třeba nalézt na tomto intervalu všechny lokální extrémy. K tomuto účelu je nejvhodnější použít tabulkovou metodu. Kromě toho je nutné vypočítat limity zkoumané funkce v krajních bodech intervalu, pokud tyto body do tohoto intervalu nepatří.

V Příkladu 1 a Úloze 1 s obrázky však nebudete muset dělat žádné výpočty.

Značení

V následujících příkladech a úlohách budeme používat tato značení:

GMax	.....	množina obsahující dvojice [xmax;ymax], kde xmax je bod, ve kterém nabývá zkoumaná funkce globální maximum, a ymax je hodnota tohoto maxima;
GMin	.....	množina obsahující dvojice [xmin;ymin], kde xmin je bod, ve kterém nabývá zkoumaná funkce globální minimum, a ymin je hodnota tohoto minima;
L(x/+)	.....	limita zadané funkce v bodě x zprava;
L(x/–)	.....	limita zadané funkce v bodě x zleva;
LKB	.....	množina obsahující hodnoty příslušných jednostranných limit v těch krajních bodech daného intervalu spojitosti, které do tohoto intervalu nepatři; týká se to otevřených a polouzavřených intervalů spojitosti; (jako „limity v krajních bodech“);
LMax	.....	množina obsahující dvojice [xmax;ymax], kde xmax je bod, ve kterém nabývá zkoumaná funkce ostré lokální maximum, a ymax je hodnota tohoto maxima;
LMin	.....	množina obsahující dvojice [xmin;ymin], kde xmin je bod, ve kterém nabývá zkoumaná funkce ostré lokální minimum, a ymin je hodnota tohoto minima;
M	.....	bod, v němž zkoumaná funkce nabývá ostré lokální maximum; v tabulce v místě pod touto značkou budeme psát hodnotu tohoto maxima;
m	.....	bod, v němž zkoumaná funkce nabývá ostré lokální minimum; v tabulce v místě pod touto značkou budeme psát hodnotu tohoto minima.

Příklad 1

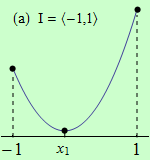
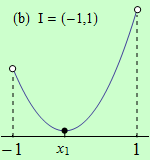
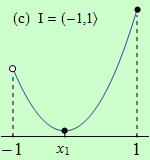
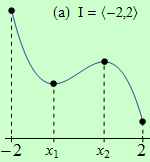
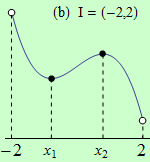
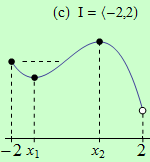
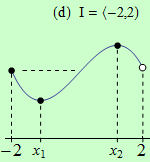
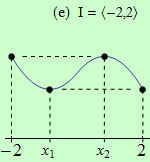
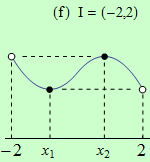
Pro funkce, jejichž grafy jsou zobrazeny v následujících obrázcích, najděte body, v nichž mají na daném intervalu I svá globální maxima a minima.

Řešení

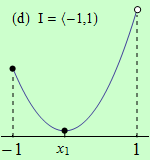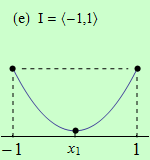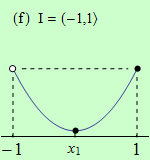Všechny funkce mají na daných intervalech globální minimum v bodě $x_1$ .

Funkce
(a) má globální maximum v bodě $x = 1$ ;
(b) nemá globální maximum;
(c) má globální maximum v bodě $x = 1$ ;
(d) nemá globální maximum;
(e) má dvě globální maxima v bodech $x = -1$ a $x = 1$ ;
(f) má globální maximum v bodě $x = 1$ .

Úloha 1

Pro funkce, jejichž grafy jsou zobrazeny v následujících obrázcích, najděte body, v nichž mají na daném intervalu I svá globální maxima a minima.

Zakrytá řešení odkryjete kliknutím na ně.

Funkce
(a)
(b)
(c)
(d)
(e)
(f)

Příklad 2

Najděte globální extrémy funkce $f: y = \cos{x}+\sin{x}$ na intervalu $\langle 0,2\pi \rangle$ .

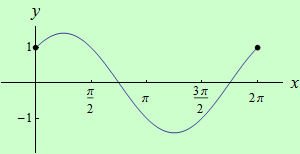graf funkce

Řešení

K nalezení lokálních extrémů použijeme tabulkovou metodu:

Intervaly spojitosti: $\langle 0,2\pi \rangle$ .
Derivace: $f^{\prime}(x) = -\sin{x} + \cos{x}$ .
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice $\sin{x} = \cos{x} \Rightarrow {\rm tg}\:x = 1$ ): $\dfrac{\pi}{4}, \dfrac{5\pi}{4}$ .
Tabulka:

$0$	$(0,\dfrac{\pi}{4})$	$\dfrac{\pi}{4}$	$(\dfrac{\pi}{4},\dfrac{5\pi}{4})$	$\dfrac{5\pi}{4}$	$(\dfrac{5\pi}{4},2\pi)$	$2\pi$
m 1	$f^{\prime}(0) = 1 \gt 0$ rostoucí	M $\sqrt{2}$	$f^{\prime}(\pi) = -1 \lt 0$ klesající	m $-\sqrt{2}$	$f^{\prime}(2\pi) = 1 \gt 0$ rostoucí	M 1

Lokální extrémy: LMax = { $[\dfrac{\pi}{4};\sqrt{2}]$ , $[2\pi;1]$ }, LMin = { $[0;1]$ , $[\dfrac{5\pi}{4};-\sqrt{2}]$ }.

Globálním maximem funkce $f$ na uzavřeném intervalu je maximum ze všech lokálních maxim a globálním minimem minimum ze všech lokálních minim.

Závěr: GMax = { $[\dfrac{\pi}{4};\sqrt{2}]$ }, GMin = { $[\dfrac{5\pi}{4};-\sqrt{2}]$ }.

Poznámka

Monotónnost funkce $f$ na intervalech $(0,\dfrac{\pi}{4})$ a $(\dfrac{5\pi}{4},2\pi)$ jsme testovali pomocí hodnoty derivací v krajních bodech, které do těchto intervalů nepatřily. Tento postup je povolený za předpokladu, že je derivace v krajním bodě definovaná a nenulová.

Úloha 2

Najděte globální extrémy funkce $f: y = -x^3+6x^2+10$ na intervalu $\langle {-1},7 \rangle$ .

K nalezení lokálních extrémů použijeme tabulkovou metodu:

Intervaly spojitosti: $\langle {-1},7 \rangle$ .
Derivace: $f^{\prime}(x) = -3x^2+12x = -3x(x-4)$ .
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice $x(x-4) = 0$ ): 0, 4.
Tabulka:

$-1$	$(-1,0)$	$0$	$(0,4)$	$4$	$(4,7)$	$7$
M 17	$f^{\prime}(-1) = -15 \lt 0$ klesající	m $10$	$f^{\prime}(1) = 9 \gt 0$ rostoucí	M $42$	$f^{\prime}(5) = -15 \lt 0$ klesající	m -39

Lokální extrémy:

Závěr: GMax = { $[4;42]$ }, GMin = { $[7;-39]$ }.

Příklad 3

Najděte globální extrémy funkce $f: y = \sqrt{x}+\dfrac{4}{x}-2$ na intervalu $(0,7 \rangle$ .

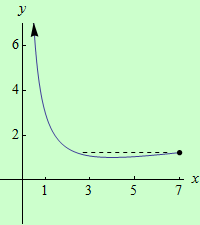graf funkce

Řešení

K nalezení lokálních extrémů použijeme tabulkovou metodu:

Intervaly spojitosti: $(0,7 \rangle$ .
Derivace: $f^{\prime}(x) =\dfrac{1}{2 \sqrt{x}}-\dfrac{4}{x^2}$ .
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice $\dfrac{1}{2 \sqrt{x}}=\dfrac{4}{x^2} \Rightarrow (\sqrt{x})^3 = 8$ ): 4.
Tabulka:

$L(0/+)$	$(0,4)$	$4$	$(4,7)$	$7$
$+\infty$	$f^{\prime}(1) = -3.5 \lt 0$ klesající	m $1$	$f^{\prime}(5) \gt 0$ rostoucí	M $\sqrt{7}-\dfrac{10}{7}$

Nerovnost $f^{\prime}(5) = \dfrac{1}{2 \sqrt{5}}-\dfrac{4}{25} \gt 0$ se řeší následovně:

$\dfrac{1}{2 \sqrt{5}} \gt \dfrac{4}{5^2} \;\;\; \Leftrightarrow \;\;\; \dfrac{1}{4\cdot 5} \gt \dfrac{16}{5^4} \;\;\; \Leftrightarrow \;\;\; 5^3 \gt 4\cdot 16 \;\;\; \Leftrightarrow \;\;\; 125 \gt 64$

Lokální extrémy: LMax = { $[7;\sqrt{7}-\dfrac{10}{7}]$ }, LMin = { $[4;1]$ }.

Musíme zohlednit limitu funkce $f$ v bodě $x = 0$ zprava: LKB = { $+\infty$ }.

Závěr: GMin = { $[4;1]$ }, globální maximum neexistuje.

Poznámka

Jestliže je příslušná jednostranná limita v krajním bodě intervalu rovna $+\infty$ , pak nemůže existovat globální maximum. Důvodem je, že žádné lokální ani globální maximum nemůže mít hodnotu plus nekonečno.

Podobně, kdyby byla příslušná jednostranná limita v krajním bodě intervalu rovna $-\infty$ , pak nemůže existovat globální minimum.

Úloha 3

Najděte globální extrémy funkce $f: y = x+\dfrac{4}{x}+5$ na intervalu $\langle {-5},0)$ .

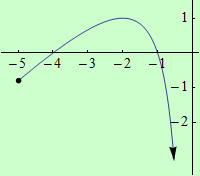graf funkce

K nalezení lokálních extrémů použijeme tabulkovou metodu:

Intervaly spojitosti: $\langle {-5},0)$ .
Derivace: $f^{\prime}(x) = 1 - \dfrac{4}{x^2}$ .
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

$-5$	$(-5,-2)$	$-2$	$(-2,0)$	$L(0/-)$
m $-0.8$	$f^{\prime}(-4) = 0.75 \gt 0$ rostoucí	M $1$	$f^{\prime}(-1) = -3 \lt 0$ klesající	$-\infty$

Lokální extrémy:

Závěr:

Úloha 4

Najděte globální extrémy funkce $f: y = -x^3+3x+1$ na intervalu $(-3,5)$ .

K nalezení lokálních extrémů použijeme tabulkovou metodu:

Intervaly spojitosti: $(-3,5)$ .
Derivace: $f^{\prime}(x) = -3x^2+3 = -3(x^2-1)$ .
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice $x^2-1 = 0$ ): -1, 1.
Tabulka:

$L(-3/+)$	$(-3,-1)$	$-1$	$(-1,1)$	$1$	$(1,5)$	$L(5/-)$
$19$	$f^{\prime}(-2) = -9 \lt 0$ klesající	m $-1$	$f^{\prime}(0) = 3 \gt 0$ rostoucí	M $3$	$f^{\prime}(2) = -9 \lt 0$ klesající	$-109$

Lokální extrémy: LMax = { $[1;3]$ }, LMin = { $[-1;-1]$ }.

Závěr: Globální extrémy neexistují.

Příklad 4

Najděte globální extrémy funkce $f: y = {\rm tg}\:x-2x$ na intervalu $(-\dfrac{\pi}{2},\dfrac{\pi}{2})$ .

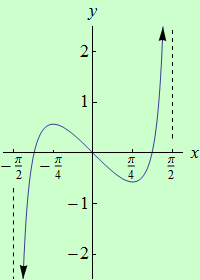graf funkce

Řešení

Všimněte si, že příslušné jednostranné limity v krajních bodech daného intervalu jsou $-\infty$ a $+\infty$ . Za této situace nemůže existovat ani globální maximum ani globální minimum. Tím je příklad vyřešen.

Derivace

Globální extrémy

Teoretická část

Příklady a úlohy

Značení

Příklad 1

Úloha 1

Příklad 2

Úloha 2

Příklad 3

Úloha 3

Úloha 4

Příklad 4

Titulní strana

Úvod

Zavedení derivace

Pravidla derivování

Monotónnost a extrémy

Konvexnost a konkávnost

L'Hospitalova pravidla

Průběh funkce

Optimalizace

Terminologie

Literatura
a webové odkazy

Tlačítka a značení

Rejstřík