Lokální extrémy tabulkovou metodou
Tato podkapitola navazuje na podkapitolu Monotónnost tabulkovou metodou. Naučíte se zde nalézat lokální extrémy různých funkcí tabulkovou metodou. Opět zde platí předpoklady uvedené v podkapitole Předpoklady, kde je také vysvětlen pojem interval spojitosti, který se v celé této podkapitole využívá.
Nejprve je uvedena teorie a pak příklady a úlohy.
Teoretická část
Definice
Funkce \(f\) má v bodě \(x_0\) lokální maximum, existuje-li takové okolí \({\rm U}(x_0)\) bodu \(x_0\), že pro všechna \(x\) z \({\rm U}(x_0) \cap D(f)\) platí: \(f(x) \leq f(x_0)\).
Funkce \(f\) má v bodě \(x_0\) lokální minimum, existuje-li takové okolí \({\rm U}(x_0)\) bodu \(x_0\), že pro všechna \(x\) z \({\rm U}(x_0) \cap D(f)\) platí: \(f(x) \geq f(x_0)\).
Definice
Platí-li v nerovnostech uvedených v předchozí definici rovnost jen pro \(x = x_0\), pak říkáme, že funkce \(f\) má v bodě \(x_0\) ostré lokální maximum, resp. ostré lokální minimum.
Lokální maximum a lokální minimum, resp. ostré lokální maximum a ostré lokální minimum, nazýváme lokální extrémy, resp. ostré lokální extrémy.
Věta
Nechť funkce \(f\) je definovaná a spojitá v nějakém okolí bodu \(x_0\).
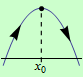
Pokud je v nějakém levém okolí tohoto bodu rostoucí a v nějakém pravém okolí tohoto bodu klesající, má funkce v tomto bodě ostré lokální maximum, viz následující obrázek:
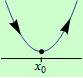
Pokud je v nějakém levém okolí tohoto bodu klesající a v nějakém pravém okolí tohoto bodu rostoucí, má funkce v tomto bodě ostré lokální minimum, viz následující obrázek:
Věta
Nechť funkce \(f\) je definovaná a spojitá v nějakém levém okolí bodu \(x_0\) a nechť existuje číslo \(\delta \gt 0\) tak, že funkce \(f\) není definovaná na otevřeném intervalu \((x_0,x_0+\delta)\). Pak platí následující dvě tvrzení:
Pokud je v nějakém levém okolí bodu \(x_0\) rostoucí, pak má funkce \(f\) v tomto bodě ostré lokální maximum, viz následující obrázky:
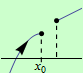
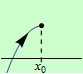
Pokud je v nějakém levém okolí bodu \(x_0\) klesající, pak má funkce \(f\) v tomto bodě ostré lokální minimum, viz následující obrázky:
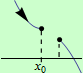
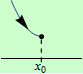
Obdobná tvrzení platí, je-li \(f\) definovaná a spojitá v nějakém pravém okolí bodu \(x_0\) a existuje-li číslo \(\delta \gt 0\) tak, že \(f\) není definovaná na otevřeném intervalu \((x_0-\delta,x_0)\).
Tabulková metoda pro hledání ostrých lokálních extrémů:
- Využije se stejné metody jako při hledání intervalů monotónnosti s tím, že se navíc uplatní výše uvedené dvě věty.
- Pozor: Omezíme-li v zadání interval, na kterém je funkce zkoumána, bereme to jako omezení definičního oboru dané funkce. Proto tomu také přizpůsobíme intervaly spojitosti, viz Příklad 2.
Příklady a úlohy
Značení
V následujících příkladech a úlohách budeme používat tato značení:
| M | ..... | bod, v němž zkoumaná funkce nabývá ostré lokální maximum; |
| m | ..... | bod, v němž zkoumaná funkce nabývá ostré lokální minimum. |
Příklad 1
Najděte body, v nichž má funkce \(f: y = x^2 + 6x + 9\) na intervalu \((-\infty,+\infty)\) ostré lokální extrémy.
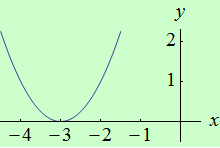 graf funkce |
Intervaly spojitosti: \((-\infty,+\infty)\).
Derivace: \(f^{\prime}(x) = 2x + 6\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(2x + 6 = 0\)): \(-3\).
Tabulka:
| \((-\infty,-3)\) | \(-3\) | \((-3, +\infty)\) |
|---|---|---|
| \(f^{\prime}(-4) = -2 \lt 0\) klesající |
m |
\(f^{\prime}(-2) = 2 \gt 0\) rostoucí |
Závěr: Funkce \(f\) má ostré lokální minimum v bodě \(x = -3\).
Úloha 1
Najděte body, v nichž má funkce \(f: y = -x^2 + 2x - 2\) na intervalu \((-\infty,+\infty)\) ostré lokální extrémy.
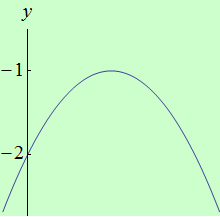 schéma grafu funkce |
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Závěr:
Příklad 2
Najděte body, v nichž má funkce \(f: y = x - e^x\) na intervalu \( \langle {-10},14)\) ostré lokální extrémy.
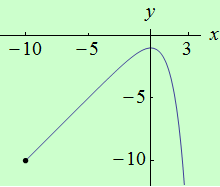 graf funkce |
Intervaly spojitosti: \( \langle {-10},14)\).
Derivace: \(f^{\prime}(x) = 1 - e^x\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(1 - e^x = 0\)): \(0\).
Tabulka:
| \(-10\) | \((-10,0)\) | \(0\) | \((0, 14)\) |
|---|---|---|---|
| m |
\(f^{\prime}(-1) = 1-{\Large\frac{1}{e}} \gt 0\) rostoucí |
M |
\(f^{\prime}(1) = 1 - e \lt 0\) klesající |
Závěr: Funkce \(f\) má ostré lokální minimum v bodě \(x = -10\) a ostré lokální maximum v bodě \(x = 0\).
Úloha 2
Najděte body, v nichž má funkce \(f: y = x e^x\) na intervalu \((-5,8 \rangle \) ostré lokální extrémy.
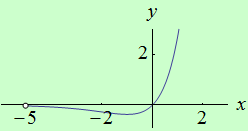 graf funkce |
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
| |
|
Závěr:
Příklad 3
Najděte body, v nichž má funkce \(f: y = 2x^3+3x^2 -12x\) na intervalu \( \langle {-7},6 \rangle \) ostré lokální extrémy.
Řešení
Intervaly spojitosti: \( \langle {-7},6 \rangle \).
Derivace: \(f^{\prime}(x) = 6(x^2+x-2)\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(x^2+x-2 = 0\)): \(-2; 1\).
Tabulka:
| \(-7\) | \((-7, -2)\) | \(-2\) | \((-2, 1)\) | \(1\) | \((1, 6)\) | \(6\) |
|---|---|---|---|---|---|---|
| m |
\(f^{\prime}(-3) = 24 \gt 0\) rostoucí |
M |
\(f^{\prime}(0) = -12 \lt 0\) klesající |
m |
\(f^{\prime}(2) = 24 \gt 0\) rostoucí |
M |
Závěr: Funkce \(f\) má ostré lokální minimum v bodě \(x = -7\) a v bodě \(x = 1\) a ostré lokální maximum v bodě \(x = -2\) a v bodě \(x = 6\).
Úloha 3
Najděte body, v nichž má funkce \(f: y = x^3-3x^2 + 3\) na intervalu \( \langle {-15},26 \rangle \) ostré lokální extrémy.
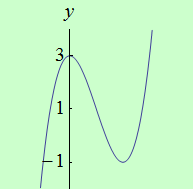 schéma grafu funkce |
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Závěr:
Příklad 4
Najděte body, v nichž má funkce \(f: y = x + \cos{x}\) na intervalu \( \langle \Large\frac{\pi}{2}\normalsize,3\pi)\) ostré lokální extrémy.
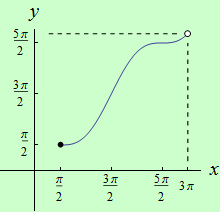 graf funkce |
Intervaly spojitosti: \( \langle \Large\frac{\pi}{2}\normalsize,3\pi)\).
Derivace: \(f^{\prime}(x) = 1-\sin{x}\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(\sin{x} = 1\)): \({\Large\frac{\pi}{2}}; 2\pi+\Large\frac{\pi}{2}\).
Tabulka:
| \(\Large\frac{\pi}{2}\) | \(({\Large\frac{\pi}{2}},2\pi+{\Large\frac{\pi}{2}} )\) | \(2\pi+\Large\frac{\pi}{2}\) | \((2\pi+{\Large\frac{\pi}{2}}, 3\pi)\) |
|---|---|---|---|
| m |
\(f^{\prime}(\pi) = 1 \gt 0\) rostoucí |
\(f^{\prime}(3\pi) = 1 \gt 0\) rostoucí |
Závěr: Funkce \(f\) má ostré lokální minimum v bodě \(x = \Large\frac{\pi}{2}\) a žádné lokální maximum.
Poznámka
Asi jste si všimli, že jsme monotónnost funkce \(f\) na intervalu \((2\pi+{\Large\frac{\pi}{2}}, 3\pi)\) testovali pomocí hodnoty derivace v krajním bodě, který do tohoto intervalu nepatří. Tento postup je povolený za předpokladu, že je derivace v krajním bodě definovaná a nenulová.
Úloha 4
Najděte body, v nichž má funkce \(f: y = x + \sin{x}\) na intervalu \((0,3\pi \rangle \) ostré lokální extrémy.
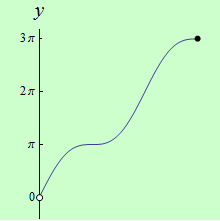 schéma grafu funkce |
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Závěr:
Příklad 5
Najděte body, v nichž má funkce \(f: y = e^x(x^2-4x+1)\) na intervalu \((-\infty,3)\) ostré lokální extrémy.
Řešení
Intervaly spojitosti: \((-\infty,3)\).
Derivace: \(f^{\prime}(x) = e^x(x^2-2x-3)\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(x^2-2x-3 = 0\)): \(-1\).
Tabulka:
| \((-\infty,-1)\) | \(-1\) | \((-1, 3)\) |
|---|---|---|
| \(f^{\prime}(-2) = 5e^{-2} \gt 0\) rostoucí |
M |
\(f^{\prime}(0) = -3 \lt 0\) klesající |
Závěr: Funkce \(f\) má ostré lokální maximum v bodě \(x = -1\) a žádné lokální minimum.
Úloha 5
Najděte body, v nichž má funkce \(f: y = e^{-x}(-x^2-5x-5)\) na intervalu \((-3,+\infty)\) ostré lokální extrémy.
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Závěr:
Příklad 6
Najděte body, v nichž má funkce \(f: y = \Large\frac{x^2+x+4}{x+1}\) na intervalu \( \langle {-3},3)\) ostré lokální extrémy.
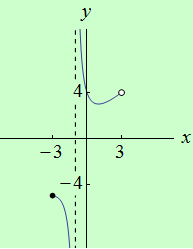 graf funkce |
Čitatel v předpisu zadané funkce lze vydělit jmenovatelem. Dostaneme, že \(y = x + \Large\frac{4}{x+1}\).
Intervaly spojitosti: \( \langle {-3}, -1)\) a \((-1, 3)\).
Derivace: \(f^{\prime}(x) = 1-\Large\frac{4}{(x+1)^2}\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(1-\Large\frac{4}{(x+1)^2}\normalsize = 0\)): \(-3; 1\).
Dvě tabulky: jedna pro interval \( \langle {-3}, -1)\) a druhá pro interval \((-1, 3)\).
|
|
Závěr: Funkce \(f\) má ostré lokální maximum v bodě \(x = -3\) a ostré lokální minimum v bodě \(x = 1\).
Úloha 6
Najděte body, v nichž má funkce \(f: y = \Large\frac{-x^2-9}{x}\) na intervalu \((-20,3 \rangle \) ostré lokální extrémy.
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Dvě tabulky:
|
|
|
Závěr:
Příklad 7
Najděte body, v nichž má funkce \(f: y = {\Large\frac{1}{x-1}}-x^3\) na intervalu \((-30,100)\) ostré lokální extrémy.
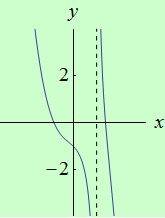 schéma grafu funkce |
Intervaly spojitosti: \((-30, 1)\) a \((1, 100)\).
Derivace: \(f^{\prime}(x) = -{\Large\frac{1}{(x-1)^2}}-3x^2\).
Poznámka: Všimněte si, že \(-{\Large\frac{1}{(x-1)^2}}\) a \(-3x^2\) jsou pro \(x \neq 1\) vždy záporná.
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti: žádné.
Dvě tabulky: jedna pro interval \((-30, 1)\) a druhá pro interval \((1, 100)\).
|
|
Závěr: Funkce \(f\) nemá žádné lokální extrémy.
Úloha 7
Najděte body, v nichž má funkce \(f: y = e^x-{\Large\frac{1}{(x+2)^3}}\) na intervalu \( \langle {-5},5 \rangle \) ostré lokální extrémy.
Intervaly spojitosti:
Derivace:
Poznámka:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti:
Dvě tabulky:
|
|
|
Závěr:
Příklad 8
Najděte body, v nichž má funkce \(f: y = -2x+e^{-2x}\) na intervalu \((-\infty,0 \rangle \) ostré lokální extrémy.
Řešení
Intervaly spojitosti: \((-\infty,0 \rangle \).
Derivace: \(f^{\prime}(x) = -2-2e^{-2x}\).
Poznámka: Všimněte si, že \(-2e^{-2x}\) je pro všechna \(x\) záporné.
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti: žádné.
Tabulka:
| \((-\infty, 0)\) | \(0\) |
|---|---|
| \(f^{\prime}(-1) \lt 0\) klesající |
m |
Závěr: Funkce \(f\) má ostré lokální minimum v bodě \(x = 0\) a žádné lokální maximum.
Úloha 8
Najděte body, v nichž má funkce \(f: y = e^{3x}+\ln{x}\) na intervalu \((1,+\infty)\) ostré lokální extrémy.
Intervaly spojitosti:
Derivace:
Poznámka:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti:
Tabulka:
Závěr:
Příklad 9
Najděte body, v nichž má funkce \(f: y = |x+2|-2\) na intervalu \((-4,1 \rangle \) ostré lokální extrémy.
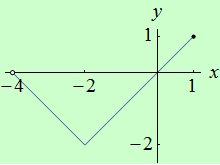 graf funkce |
Intervaly spojitosti: \((-4,1 \rangle \).
Derivace: \(f^{\prime}(x) = -1\) pro \(x \lt -2\) a \(f^{\prime}(x) = 1\) pro \(x \gt -2\).
Body z intervalů spojitosti, v nichž není derivace definována: \(-2\).
Stacionární body z intervalů spojitosti (řešení rovnice \(f^{\prime}(x) = 0\)): žádné.
Tabulka:
| \((-4, -2)\) | \(-2\) | \((-2, 1)\) | \(1\) |
|---|---|---|---|
| \(f^{\prime}(-3) = -1 \lt 0\) klesající |
m |
\(f^{\prime}(-1) = 1 \gt 0\) rostoucí |
M |
Závěr: Funkce \(f\) má ostré lokální minimum v bodě \(x = -2\) a ostré lokální maximum v bodě \(x = 1\).
Úloha 9
Najděte body, v nichž má funkce \(f: y = 3-|x-1|\) na intervalu \( \langle {-1},2 \rangle \) ostré lokální extrémy.
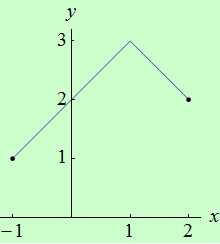 graf funkce |
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Závěr: