Monotónnost a extrémy - předpoklady
V této podkapitole jsou uvedeny tři předpoklady, které platí pro celou kapitolu. Účelem těchto předpokladů je zjednodušení výkladu látky. Bez nich by se stal výklad náročný a možná i nepřehledný, protože by bylo nutné rozebírat v příkladech mnoho různých speciálních případů.
Budeme-li mluvit o monotónních funkcích, budeme mít vždy na mysli pouze rostoucí nebo klesající funkce.

Z hlediska monotónnosti a extrémů budeme vyšetřovat pouze takové funkce, jejichž předpis je tvořen elementárními funkcemi uvedenými v kapitole Pravidla derivování, podkapitole Úvod, nebo i absolutní hodnotou, jejich složením, a operacemi plus, mínus, krát a děleno.
V dalších dvou předpokladech se používá následující pojem:
Interval spojitosti funkce \(f\) je libovolný interval \(I \subset \mathbb R\), který patří do definičního oboru funkce \(f\), na němž je funkce \(f\) spojitá. Pozor: Nevyplývá-li ze zadání příkladu či úlohy něco jiného, bereme za intervaly spojitosti maximální takové intervaly, to jest takové intervaly, které kdyby se více zvětšily, tak by přestaly mít požadované vlastnosti.
Jak zjišťujeme intervaly spojitosti:- Nejprve je třeba stanovit definiční obor zadané funkce. Pak z definičního oboru této funkce vyčteme, jaké intervaly tento obor obsahuje. Tyto intervaly jsou intervaly spojitosti zadané funkce.
- Metoda uvedená v předchozím bodě platí, jedná-li se o typ funkce uvedený v Předpokladu 2.
Ilustrace
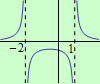
Funkce \(f: y = \frac{1}{(x+2)(x-1)}\) má definiční obor \(D(f) = \mathbb R \setminus \{-2, 1\}\). Ten se dá zapsat jako sjednocení tří intervalů: \(D(f) = (-\infty,-2) \cup (-2,1) \cup (1,+\infty)\). Intervaly spojitosti dané funkce tedy jsou \((-\infty, -2)\), \((-2, 1)\) a \((1, +\infty)\). Žádný z těchto intervalů spojitosti se nedá více zvětšit. Pokud by byl některý z nich zvětšen, přestal by být intervalem spojitosti.
Z hlediska monotónnosti a extrémů budeme vyšetřovat pouze takové funkce, na jejichž intervalech spojitosti, resp. intervalu spojitosti, je nulový nebo malý konečný počet bodů, v nichž je derivace nulová (tzv. stacionární body), a bodů, v nichž není derivace definovaná.
Předpoklad 4
Funkce budeme vyšetřovat z hlediska monotónnosti a extrémů pouze na jejich intervalech spojitosti. Mimo tyto intervaly je budeme považovat pro tento účel za nedefinované.