Jednoduché úročení
V této kapitole se budeme věnovat úročení. Úročení je způsob, jak počítat úroky. Rozlišujeme dva základní typy úročení, a to jednoduché a složené úročení.
Důležité u úročení je časové období, ke kterému se vztahuje výpočet úroku.
Definice
Úrokovací období je časový úsek mezi dvěma bezprostředně po sobě následujícími úročeními. Úrokovací období může být roční, pololetní, čtvrtletní, měsíční, denní, ...
Definice
Jednoduché úročení je takový způsob úročení, při kterém se úrok na konci každého úrokovacího období počítá z počátečního kapitálu.
Poznámka
Pokud úrokovací doba není dělitelná beze zbytku úrokovacím obdobím, pak na zbylé necelé období použijeme některý ze standardů.
Zkusme vyjít z definice jednoduchého úročení a spočítejme na konkrétním příkladu částku, kterou budeme mít po třech letech. Pro zjednodušení situace nebudeme uvažovat daň z úroku a úrokovací období je rok.
Příklad
Na začátku roku 2019 vložíme 1 000 000 Kč na 3 roky na bankovní účet. Banka uvádí roční úrokovou sazbu 1 %, úrokovací období je rok. Banka používá jednoduché úročení. Neuvažujme daň z úroku. Jak velká bude výsledná naspořená částka po třech letech?
Řešení
Řešení je uvedeno v tabulce 2.1.1.
| Vždy na konci roku | |||
|---|---|---|---|
| Rok | Úrok v Kč | Celkový úrok v Kč | Stav účtu v Kč |
| 2019 | \(1\,000\,000\cdot\frac{1}{100}=10\,000\) | \(10\,000\) | \(1\,000\,000+10\,000\) |
| 2020 | \(1\,000\,000\cdot\frac{1}{100}=10\,000\) | \(10\,000+10\,000=2\cdot10\,000\) | \(1\,000\,000+2\cdot10\,000\) |
| 2021 | \(1\,000\,000\cdot\frac{1}{100}=10\,000\) | \(2\cdot10\,000+10\,000=3\cdot10\,000\) | \(1\,000\,000+3\cdot10\,000\) |
Na konci roku 2021 (po třech letech) bude výsledný kapitál \(1\,000\,000\,\text{Kč}+3\cdot10\,000\,\text{Kč}=1\,030\,000\,\text{Kč}\).
Obr. 2.1.1 ilustruje průběh jednoduchého úročení. Ukazuje, jak se mění kapitál v jednotlivých úrokovacích obdobích.
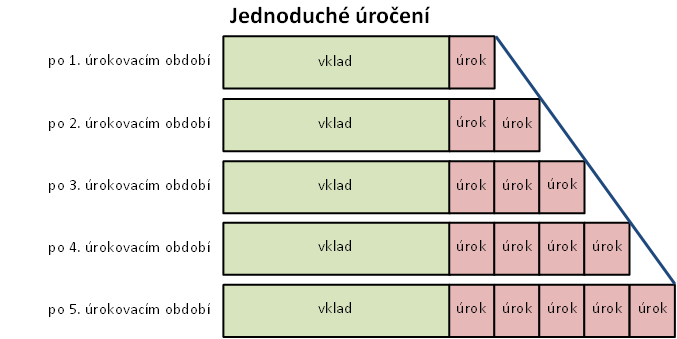Obr. 2.1.1
Odvození vzorce pro jednoduché úročení
Nyní si odvodíme vzorec pro jednoduché úročení. Opět si situaci zjednodušíme a budeme uvažovat roční úrokovací období a nebudeme počítat s daní z úroku. Různým frekvencím úročení a dani z úroku se budeme věnovat v samostatných následujících kapitolách.
Příklad
Uvažujme bankovní účet, na který vložíme počáteční kapitál \(K_0\), úrokovací období je 1 rok. Banka používá jednoduché úročení a uvádí roční úrokovou sazbou \(i\). Neuvažujte daň z úroku.
Jaký bude výsledný kapitál \(K_n\) na účtě po \(n\) letech?
Řešení
Řešení je uvedeno v tabulce 2.1.2.
| Na konci úrokovacího období | |||
|---|---|---|---|
| Čas | Úrok v Kč | Kumulovaný úrok v Kč | Stav účtu v Kč |
| \(0\) | \(K_0\) | ||
| \(1\) | \(K_0 \cdot i\) | \(K_0\cdot i\) | \(K_0+K_0\cdot i = K_0(1+i)\) |
| \(2\) | \(K_0 \cdot i\) | \(2 K_0 \cdot i\) | \(K_0+K_0\cdot 2i = K_0(1+2i)\) |
| \(3\) | \(K_0 \cdot i\) | \(3 K_0 \cdot i\) | \(K_0+K_0\cdot 3i = K_0(1+3i)\) |
| \(\dots\) | \(\dots\) | \(\dots\) | \(\dots\) |
| \(n\) | \(K_0 \cdot i\) | \(n K_0 \cdot i\) | \(K_0+K_0\cdot ni = K_0(1+in)\) |
Po \(n\) letech bude výsledný kapitál \(K_n=K_0(1+in)\).
Věta
Výsledný kapitál \(K_n\) po \(n\) ročních úrokovacích obdobích, který je úročen jednoduchým úročením s roční úrokovou sazbu \(i\) a úrokovací období je 1 rok, spočítáme následovně
Poznámka
Stejný vzorec by platil i v případě, kdybychom měli měsíční (týdenní, denní, ...) úrokovou sazbu \(i\) a vklad bychom úročili měsíčně (týdenně, denně, ...). Pak by ale \(K_n\) byla částka po \(n\) měsících (týdnech, dnech, ...).
V kapitole Frekvence úročení se budeme zabývat případem, kdy je dána roční úroková sazba, ale úročili bychom vícekrát do roka, tj. úrokovací období bude kratší než rok.
Abychom si lépe představili, jak roste kapitál při jednoduchém úročení, uvádíme zde graf v Appletu 2.1.1, kde lze měnit úrokovou sazbu.
Úloha
Na začátku roku vložíme na bankovní účet \(1\,000\,000\,\text{Kč}\) na 5 let.
Úrokovací období je jeden rok a roční úroková sazba je \(1,2\,\%\).
Daň z úroku neuvažujte.
Banka úročí kapitál pomocí jednoduchého úročení.
Jaký bude výsledný kapitál po pěti letech?
Vliv daně na výsledný kapitál při jednoduchém úročení si uvedeme v kapitole Vliv daně a inflace.
