Úmor
V této kapitole se budeme věnovat výši úroku a snižování dlužné částky.
Definice
Úmor dluhu je ta část splátky úvěru (dluhu), která snižuje dlužnou částku.
Splátka každého úvěru se skládá z úmoru a úroku.
Na následujícím příkladu si ukážeme, jak se anuitní splátka rozkládá na úrok a úmor. Využijeme stejný příklad jako v podkapitole Motivace.
Příklad
Půjčíme si v bance 1 milion Kč s roční úrokovou sazbou 3 %. Úrokovací období u půjčky bude rok a částku budeme chtít splatit ve třech ročních anuitních splátkách. Označíme \(s\) částku, kterou budeme splácet.
Jaký je úrok a úmor v jednotlivých splátkách?
Řešení
Z motivačního příkladu známe vztah pro splátku \(s\). Splátku \(s\) lze také spočítat již z odvozeného vztahu pro anuitní splátku.
\(s=\displaystyle\frac{V\cdot i}{1-(1+i)^{-n}}=\displaystyle\frac{1\,000\,000\text{ Kč}\cdot 0,03}{1-(1+0,03)^{-3}}\approx \)\(353\, 531\text{ Kč}\).
Jak se postupně mění úrok a úmor v tomto příkladu, je zobrazeno v následující tabulce 4.4.1.
| Rok | Dluh na začátku v Kč | Úrok v Kč | Úmor v Kč | Dluh na konci v Kč |
|---|---|---|---|---|
| 0 | \(1\,000\,000\) | |||
| 1 | \(10^6\)\(\cdot 1,03=1\,030\,000\) | \(10^6\cdot 1,03-10^6=\) \(30\,000\) | \(353\, 531\)\(-30\,000=\) \(323\,531\) | \(10^6\cdot 1,03-\)\(353\, 531=\) \(676\,469\) |
| 2 | \(676\,469\)\(\cdot 1,03 \approx 696\,763\) | \(696\,763-676\,469=\) \(20\,294\) | \(353\, 531\)\(-20\,294=\) \(333\,237\) | \(696\,763-\)\(353\, 531\) \(=\)\(343\,232\) |
| 3 | \(343\,232\)\(\cdot 1,03 \approx 353\,528\) | \(353\,528-343\,232=\) \(10\,296\) | \(343\,232\) | 0 |
Poslední splátka je menší než ostatní, a to z důvodu zaokrouhlování.
Na následujícím grafu na obr 4.4.1 je graficky zobrazen poměr úmoru a úroku v jednotlivých splátkách.
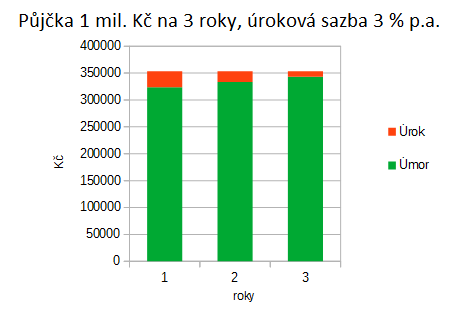Obr. 4.4.1
Platí, že úrok klesá a úmor roste s rostoucím počtem úrokovacích období. Při bezúročné půjčce se úmor rovná výši splátky.
Abychom si lépe ukázali, jak se mění úrok a úmor, zvyšme v následujícím příkladu počet splátek.
Příklad
Půjčíme si v bance 1 milion Kč s roční úrokovou sazbou 3 %. Úrokovací období u půjčky bude rok a částku budeme chtít splatit v deseti ročních anuitních splátkách. Označíme \(s\) částku, kterou budeme splácet.
Graficky znázorněte úrok a úmor v jednotlivých splátkách.
Řešení
Splátku \(s\) spočítáme pomocí již odvozeného vztahu pro anuitní splátku.
\(s=\displaystyle\frac{V\cdot i}{1-(1+i)^{-n}}=\displaystyle\frac{1\,000\,000\text{ Kč}\cdot 0,03}{1-(1+0,03)^{-10}}\approx\)\(117\, 231\text{ Kč}\)
Na následujícím grafu na obr. 4.4.2 je zobrazen poměr úmoru a úroku v jednotlivých splátkách.
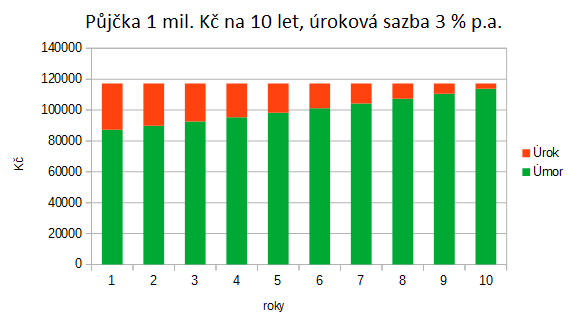Obr. 4.4.2
