Objem jehlanu
V této kapitole si představíme, jak se počítá objem jehlanu. Pro odvození vzorce pro objem jehlanu vycházíme z objemu krychle o hraně délky a.
Tedy objem V krychle o hraně délky a je
V =a³.
Vzorec pro objem jehlanu můžeme nastínit rozdělením krychle na šest shodných čtyřbokých jehlanů (obr. 4.6.1). Jelikož podstava každého ze šesti čtyřbokých jehlanů je zároveň jednou stěnou krychle, bude se jednat o pravidelné čtyřboké jehlany. Mají jediný společný bod – hlavní vrchol, který je umístěný ve středu neboli těžišti krychle (bod S), tedy jejich výška je \frac{a}{2}. Na následujícím appletu (obr. 4.6.1) táhněte bodem B po kruhovém oblouku pro rozložení krychle na šest nepronikajících se shodných pravidelných čtyřbokých jehlanů.
Obrázek 4.6.1: Applet – krychle rozdělená na šest shodných pravidelných čtyřbokých jehlanů
Krychli lze tedy složit z šesti shodných pravidelných čtyřbokých jehlanů o podstavné hraně a, tělesové výšce \frac{a}{2}. Můžeme tedy vyjádřit objem V_j jednoho jehlanu pomocí objemu V_k krychle o hraně a, tedy
V_j=\frac{V_k}{6}=\frac{a^3}{6}.
Pro objem V_j dílčího pravidelného jehlanu, jehož podstava je čtverec o straně a (S_p=a^2) a jehož výška v je \frac{a}{2}, platí
V_j=\frac{a^3}{6}=\frac{1}{3} \cdot a^2 \cdot \frac{a}{2} = \frac{1}{3} S_p v.
Odvození vzorce pro objem n-bokého jehlanu
Pomocí krychle si také odvodíme objem trojbokého jehlanu. Nejprve si ještě ukážeme, že objem čtyřbokého jehlanu, který není pravidelný, lze odvodit obdobně jako pro pravidelný čtyřboký jehlan. Krychli ABCDEFGH rozdělíme na tři shodné nepronikající se jehlany CDABH, GCBFH a BAEFH se čtvercovou podstavou o straně a a tělesovou výškou rovněž délky a (obr. 4.6.2). Podle první vlastnosti objemu se jejich objemy rovnají a podle druhé vlastnosti objemu platí, že objem krychle je součtem objemů těchto tří čtyřbokých jehlanů. Tedy objem V tohoto čtyřbokého jehlanu se čtvercovou podstavou je roven třetině objemu původní krychle. Na následujícím appletu (obr. 4.6.2) táhněte bodem G po kruhovém oblouku pro rozložení krychle na tři nepronikající se jehlany se čtvercovou podstavou.
Obrázek 4.6.2: Applet – krychle rozdělená rovinami ABH, BCH a BFH na tři čtyřboké jehlany
Z předchozího tvrzení vyplývá, že pokud podstava je čtverec o straně a (S_p=a^2) a tělesová výška je též délky a, tak pro objem uvedeného čtyřbokého jehlanu platí
V=\frac13a³ =\frac13a² \cdot a = \frac{1}{3} S_p v.
Nyní zvolíme kolmý trojboký hranol KLMNOP namísto krychle a pomocí něho odvodíme vzorec pro objem trojbokých jehlanů. Tento kolmý trojboký hranol \mathcal{H} rozdělíme na tři nepronikající se trojboké jehlany KLMN, NOPL a LMPN (obr. 4.6.3). Víme podle druhé vlastnosti objemu, že objem celého kolmého trojbokého hranolu je roven součtu objemů tří trojbokých jehlanů:
V(\mathcal{H})=V(KLMN)+V(NOPL)+V(LMPN).
Nyní budeme zjišťovat, zda tři nepronikající se trojboké jehlany KLMN, NOPL a LMPN mají stejné objemy. Nejdříve dokážeme rovnost objemů trojbokých jehlanů KLMN, NOPL. Objemy jehlanů KLMN a NOPL se rovnají, neboť jehlany jsou shodné, jelikož podstavami obou jehlanů jsou shodné trojúhelníky KLM a NOP a jehlany mají zárověň shodné všechny boční stěny. Vycházíme z první vlastnosti objemu, která uvádí že, shodná tělesa mají sobě rovné objemy a platí
V(KLMN)=V(NOPL).
Dále potřebujeme dokázat rovnost objemů trojbokých jehlanů NOPL a LMPN. Trojboký jehlan NOPL s podstavou NOP a hlavním vrcholem v bodě L překlopíme na trojboký jehlan s podstavou LOP a hlavním vrcholem v bodě N.
Objemy jehlanů LOPN a LMPN se rovnají, neboť platí Cavalieriho princip, jelikož podstavami obou jehlanů jsou shodné trojúhelníky LOP a LMP (protože rovnoběžník LMOP je rozdělený stěnovou úhlopříčkou LP na dva shodné trojúhelníky – podstavy LOP a LMP); dále mají stejnou tělesovou výšku (protože tyto dva trojboké jehlany dohromady tvoří čtyřboký jehlan LMOPN s podstavou LMOP a hlavním vrcholem v bodě N). Platí
V(LOPN)=V(LMPN).
Tím jsme dokázali, že tři trojboké jehlany KLMN, NOPL a LMPN mají stejný objem. Jelikož se jejich objemy rovnají, tak pro trojboké jehlany platí
V=\frac13V(H) =\frac13 S_pv.
Obrázek 4.6.3: Applet – trojboký hranol \mathcal{H} rozdělený na tři trojboké jehlany KLMN, NOPL a LMPN
Pro určení objemu n-bokého jehlanu (n>3) využijeme Cavalieriho princip. Mějme dán trojboký nebo čtyřboký jehlan se čtvercovou podstavou a další n-boký tak, že podstavy daných jehlanů mají stejný obsah podstavy S_p a stejnou výšku v. Umístíme je do roviny \rho. Mnohoúhelníky vzniklé řezem jehlanů rovinou \sigma, \sigma \parallel \rho, jsou stejnolehlé s podstavami jehlanů, a tedy podobné. Středy stejnolehlostí jsou umístěny v hlavních vrcholech těchto jehlanů. Koeficient podobnosti je u těchto řezů stejný, platí
k=\frac {v_1} {v},

kde {v} je vzdálenost hlavních vrcholů jehlanů od roviny \rho jejich podstav a {v_1} je vzdálenost hlavních vrcholů jehlanů od roviny řezu \sigma. S využitím stejnolehlosti dostáváme vztah mezi obsahem řezu S a obsahem podstavy S_p:
S=k^2S_p.
Díky rovnosti obsahů podstav a stejnému koeficientu podobnosti k u obou jehlanů platí i rovnost pro obsahy řezů. Z Cavalieriho principu vyplývá, že tyto jehlany mají stejný objem, tj. i pro n-boký jehlan platí
V=\frac13S_pv.
Uvažujme konvexní pravidelný trojboký, konvexní nepravidelný čtyřboký a nekonvexní pětiboký jehlan o stejné výšce, jejichž podstavy leží ve stejné rovině a mají stejný obsah (veličiny jsou uvedeny bez jednotek), viy obr. 4.6.4. Řezy těmito třemi jehlany vedené rovnoběžně s rovinou jejich podstav v libovolné výšce jsou vždy podobné s podstavou, protože rovina řezu je s ní rovnoběžná. Tudíž objemy těchto jehlanů jsou si rovny. Změnou polohy bodu H měníme výšku v_1. Změnou polohy bodu A"_1 měníme výšku všech jehlanů. Můžeme pozorovat, že změnami poloh těchto bodů se obsahy řezů hranolů nemění.
Obrázek 4.6.4: Applet – využití Cavalieriho principu a stejnolehlosti pro tři jehlany se stejnými obsahy podstav Sp a se stejnými výškami v
Předchozí úvahy můžeme nyní shrnout.
Objem V libovolného jehlanu s tělesovou výškou v a obsahem podstavy S_p je dán vztahem
V = \frac{1}{3}S_pv.
Příklad 4.6.1
Vypočítejte objem V_j pravidelného čtyřbokého jehlanu ABCDV. Jeho boční stěny jsou tvořené shodnými rovnostrannými trojúhelníky o straně délky a = 5 cm, bod T je středem jeho podstavy. Výsledek zaokrouhlete na jedno desetinné místo.
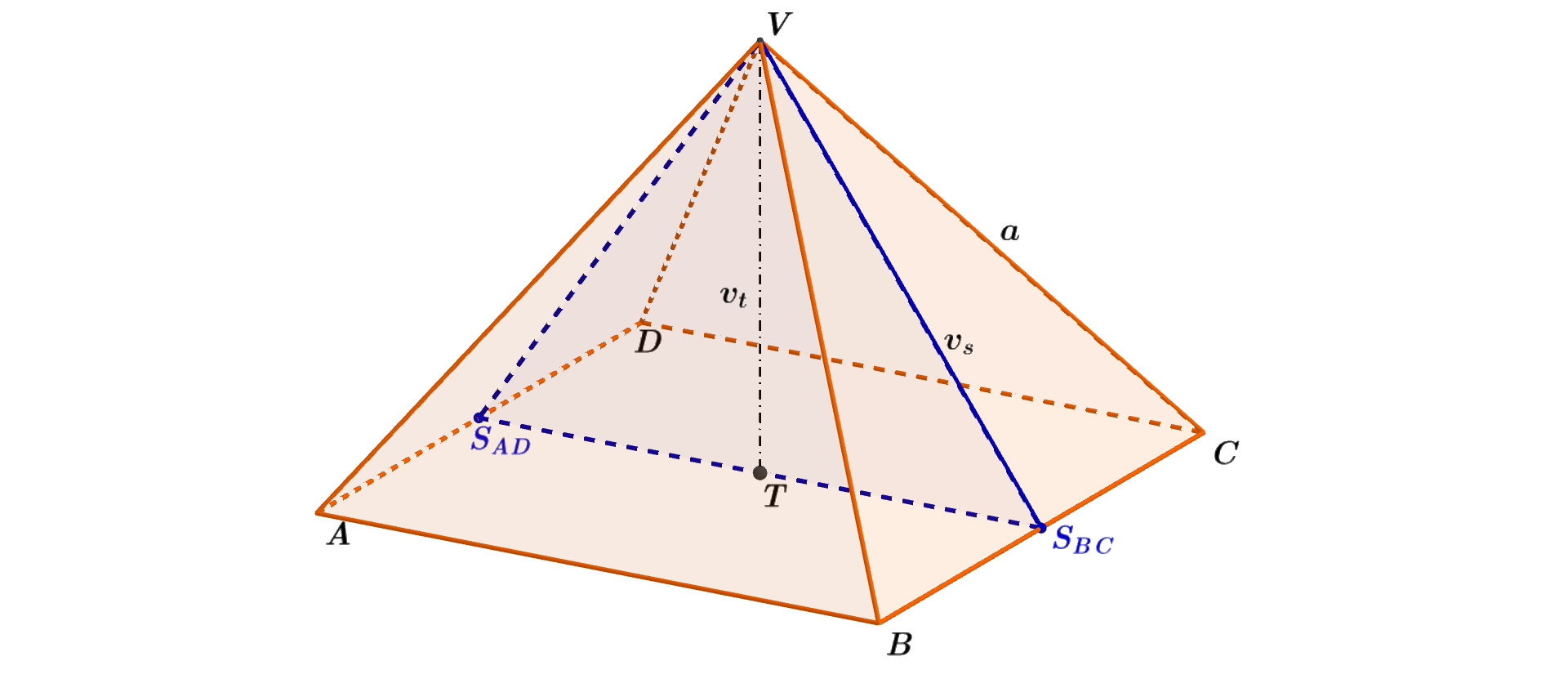
Obrázek 4.6.5: Ilustrace Příkladu 4.6.1
Řešení
- Pro výpočet objemu V_j jehlanu potřebujeme znát obsah podstavy S_p a jeho výšku v_t.
- Jsou-li boční stěny pravidelného čtyřbokého jehlanu navzájem shodné rovnostranné trojúhelníky, tak podstavou jehlanu je čtverec ABCD o straně a=5 cm (obr. 4.6.5).
- Obsah čtvercové podstavy S_p= a^2 = 25 cm^2.
- Tělesovou výšku v_t určíme například pomocí rovnoramenného \triangle S_{BC} S_{AD} V. Vyjádříme délku jeho stran.
- |S_{BC} S_{AD}|=a; |T S_{BC}| =\frac{1}{2}a.
- Pro délku stěnové výšky v_s (v_s=|S_{BC} V|) každé boční stěny platí v_s=a\frac{\sqrt3}{2}. Tuto hodnotu vypočítáme Pýthagorovou větou například z rovnostranného \triangle BCV, který rozdělíme pomocí v_s na dva pravoúhlé trojúhelníky.
- Z pravoúhlého \triangle V T S_{BC} pomocí Pýthagorovy věty vyjádříme délku v_t; v_t = \sqrt{(({a\frac{\sqrt3}{2}})^2 - (\frac{a}{2})^2)} = \frac{a\sqrt2}{2} = \frac{5\sqrt2}{2} cm.
- Pro objem jehlanu platí: V_j = \frac{1}{3}S_pv_t = \frac{1}{3} \cdot 25 \cdot \frac{5\sqrt2}{2} cm^3 = \frac{5^3\sqrt2}{6} cm^3 \doteq 29,5 cm^3.
- Objem pravidelného čtyřbokého jehlanu ABCDV je po zaokrouhlení 29,5 cm^3.
Příklad 4.6.2
Vypočítejte objem V_j pravidelného čtyřbokého jehlanu ABCDV. Jeho boční stěny jsou tvořené shodnými rovnoramennými trojúhelníky se základnami délky a = 4 \sqrt6 cm a rameny délky q = 7 cm.
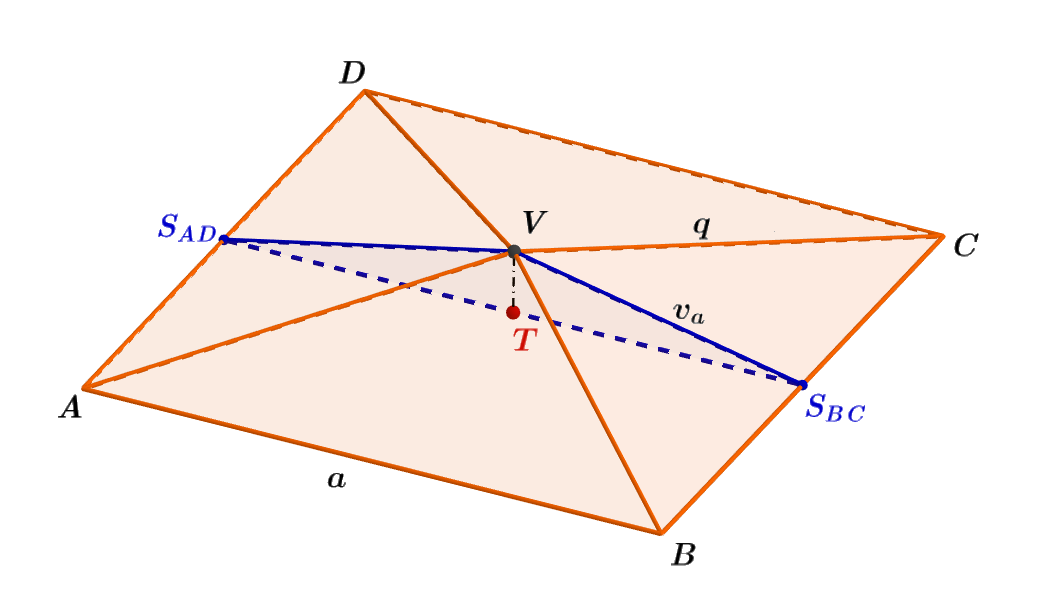
Obrázek 4.6.6: Ilustrace Příkladu 4.6.2
Řešení
- Pro výpočet objemu V_j jehlanu potřebujeme znát obsah podstavy S_p a výšku v_{t}.
- Jsou-li boční stěny pravidelného čtyřbokého jehlanu tvořeny rovnoramennými trojúhelníky se základnou délky a = 4 \sqrt6 cm a rameny délky q = 7 cm, tak podstava jehlanu ABCD je čtverec o straně délky a (obr. 4.6.6).
- S_p=a^2=(4 \sqrt6)^2 cm^2 = 96 cm^2.
- Tělesová výška v_{t} jehlanu je zárověň vyškou k základně rovnoramenného \triangle S_{AD}S_{BC}V. Základna tohoto trojúhelníku je rovna a = |S_{AD}S_{BC}| = 4 \sqrt6 cm.
- Ramena rovnoramenného \triangle S_{AD}S_{BC}V vypočítáme z pravoúhlého \triangle S_{BC}CV, kde pomocí Pýthagorovy věty určíme v_a;
|S_{AD}V| = |VS_{BC}| = v_a = \sqrt {q^2 - (\frac{a}{2})^2 } = \sqrt {7^2 - (\frac{4\sqrt6}{2})^2} cm = \sqrt {25} cm = 5 cm. - Délku tělesové výšky v_{t} vypočítáme z pravoúhlého \triangle VTS_{BC}, kde pomocí Pýthagorovy věty určíme v_t;
|VT| = v_t = \sqrt {(v_a)^2 - (\frac{a}{2})^2 } = \sqrt {5^2 - (\frac{4\sqrt6}{2})^2} cm= \sqrt {1} cm= 1 cm. - Pro objem jehlanu platí: V_j = \frac{1}{3}S_pv_t = \frac{1}{3} \cdot 96 \cdot 1 cm^3 = 32 cm^3.
- Objem pravidelného čtyřbokého jehlanu ABCDV je 32 cm^3.
Příklad 4.6.3
Je dán čtyřboký jehlan RSTUV, jehož podstavou je rovnoramenný lichoběžník o základnách délky a = 8 dm, c = 4,5 dm a dvěma rameny délky b = 4,3 dm. Pro výšku v_p rovnoramenného lichoběžníku platí v_p = 4 dm. Výška jehlanu měří 4,97 dm. Vypočítejte objem V_j tohoto jehlanu. Výsledek uveďte na dvě desetinná místa.
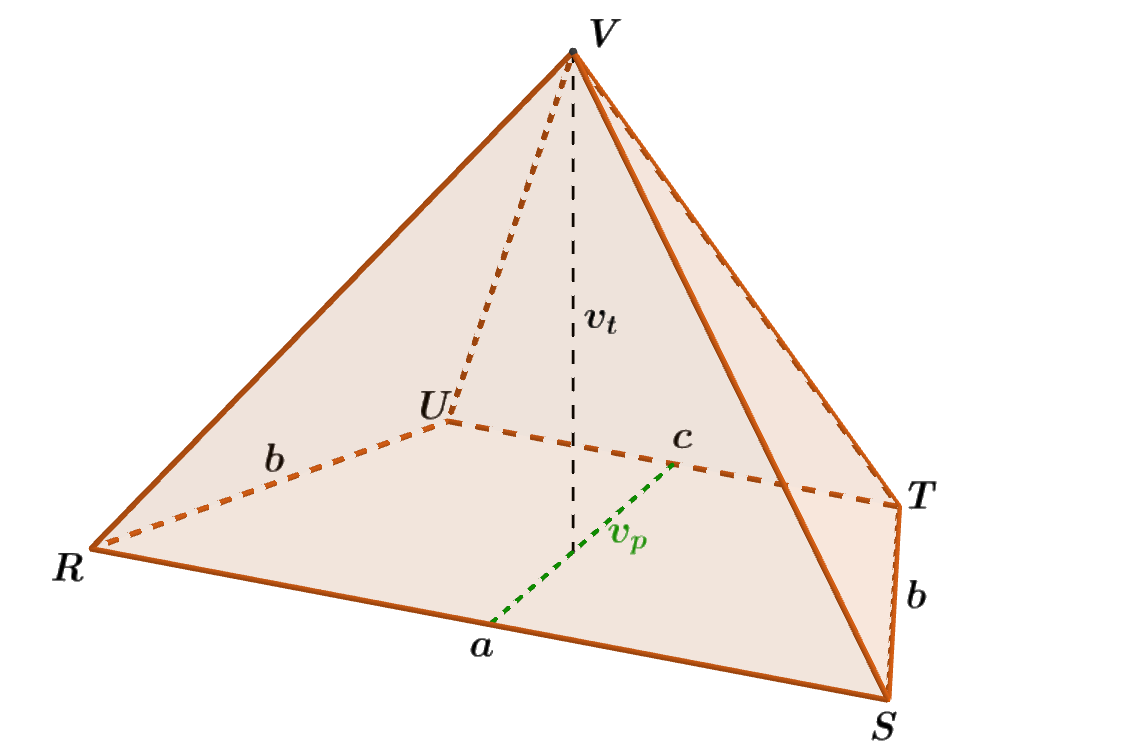
Obrázek 4.6.7: Ilustrace Příkladu 4.6.3
Řešení
- Pro výpočet objemu V_j jehlanu potřebujeme znát obsah podstavy S_p a jeho výšku v_t.
- Pro obsah podstavy S_p ve tvaru lichoběžníku platí S_p = \frac{(a\ +\ c)\ \cdot\ v_p}{2} = \frac{(8\ +\ 4,5)\ \cdot\ 4}{2} dm^2 = 25 dm^2.
- Výška jehlanu v_t = 4,97 dm (obr. 4.6.7).
- Pro objem jehlanu platí: V_j = \frac{1}{3}S_pv_t = \frac{1}{3} \cdot 25 \cdot 4,97 dm^3 \doteq 41,42 dm^3.
- Objem čtyřbokého jehlanu RSTUV je 41,42 dm^3.
Příklad 4.6.4
Je dán pětiboký jehlan KLMNOV, jehož podstavou je pravidelný pětiúhelník o straně a = 10 m. Výška v_t jehlanu měří 8,42 m. Určete jeho objem V_j. Výsledek zaokrouhlete na dvě desetinná místa.
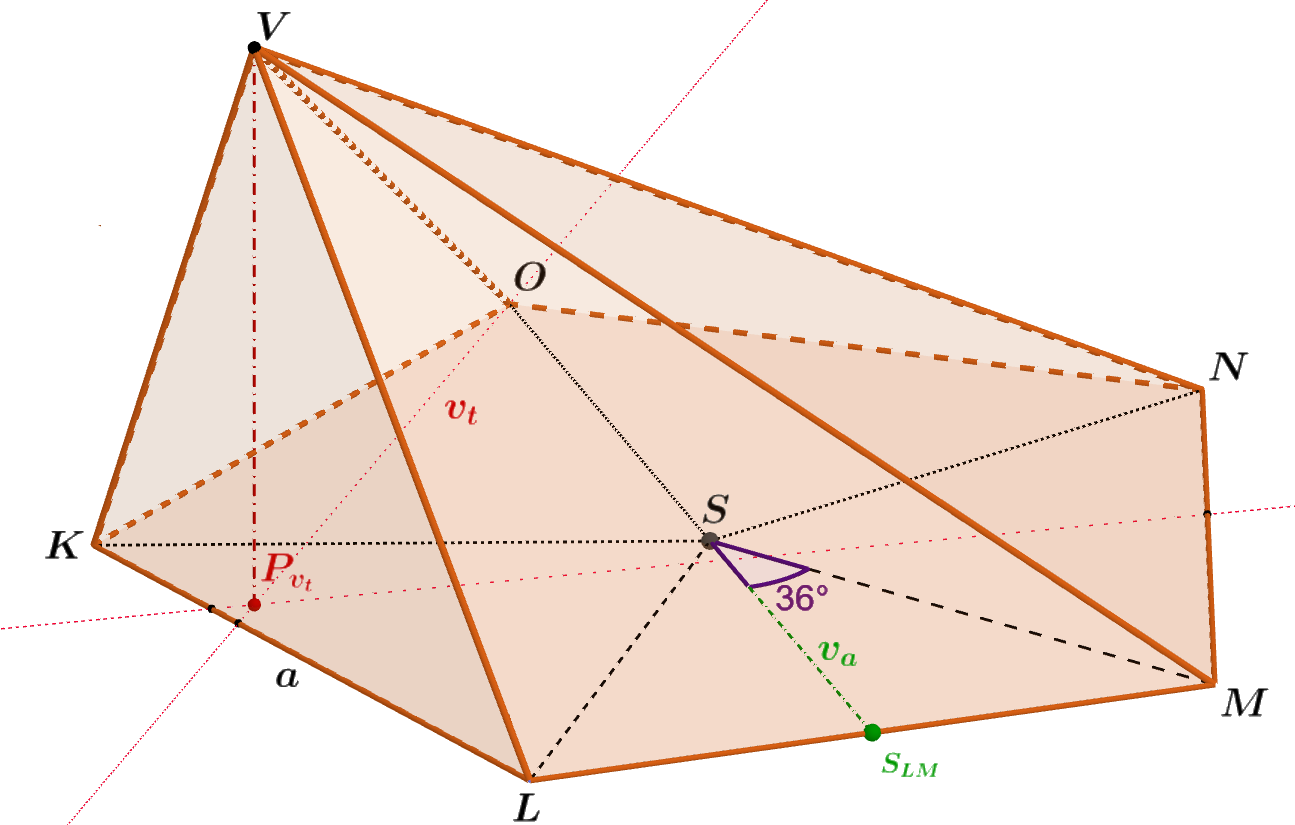
Obrázek 4.6.8: Ilustrace Příkladu 4.6.4
Řešení
- Pro výpočet objemu V_j jehlanu potřebujeme znát obsah podstavy S_p a jeho výšku v_t = 8,42 m.
- Podstavou daného jehlanu je pravidelný pětiúhelník o straně a=10 m. Pravidelný pětiúhelník rozložíme na pět shodných rovnoramenných trojúhelníků (obr. 4.6.8); S_{\triangle LMS} = \frac{a v_a}{2}.
Z \triangle SS_{LM}M vyjádříme v_a; v_a = \cot 36° \cdot \frac {a}{2} \doteq 1,376 \cdot 5 m \doteq 6,882 m.
Tedy S_{\triangle LMS} = \frac{10\ \cdot\ 6,882}{2} m^2 \doteq 34,410 m^2; S_p = 5 \cdot S_{\triangle LMS} = 5 \cdot 34,410 m^2 = 172,050 m^2. - Výška jehlanu v_t = 8,42 m.
- Pro objem jehlanu platí: V_j = \frac{1}{3}S_pv_t = \frac{1}{3} \cdot 172,050 \cdot 8,42 m^3 \doteq 482,89 m^3.
- Objem pětibokého jehlanu KLMNOV je po zaokrouhlení 482,89 m^3.
Příklad 4.6.5
Je dán nekonvexní desetiboký jehlan KELAMBNCODV. Podstavou tohoto jehlanu je pentagram, tj. pěticípý nekonvexní hvězdicovitý mnohoúhelník se stranami stejné délky. Pentagram vznikl z pravidelného konvexního pětiúhelníku o straně a = 5 m. Výška v_t jehlanu je 8,55 m. Určete jeho objem V_j. Výsledek zaokrouhlete na dvě desetinná místa.
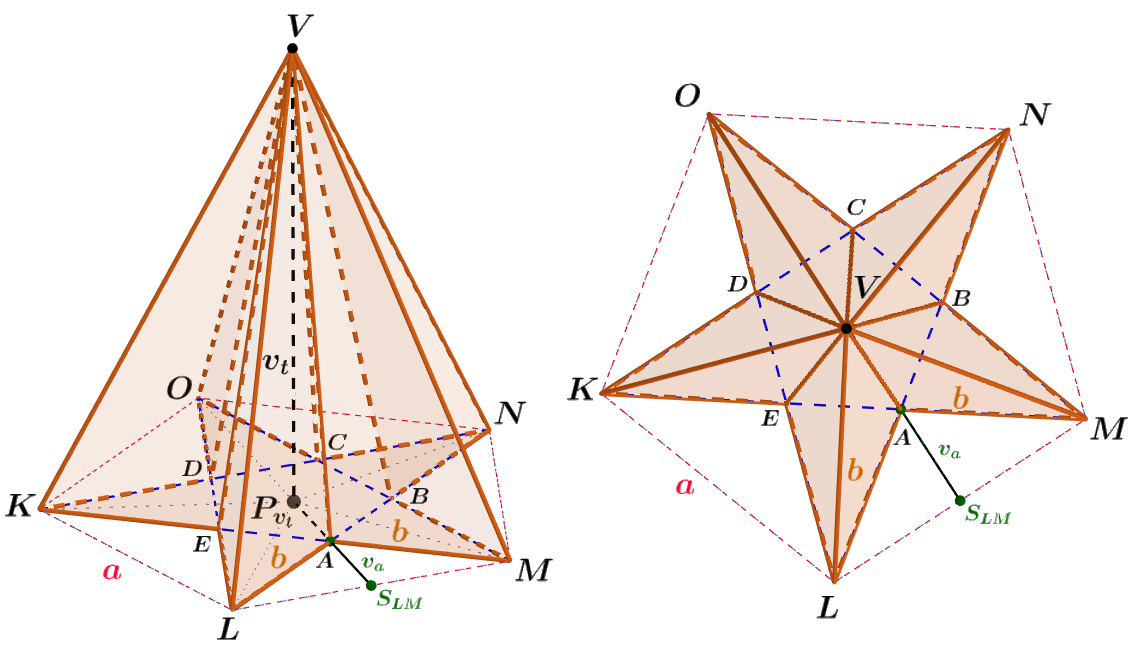
Obrázek 4.6.9: Ilustrace Příkladu 4.6.5
Řešení
- Pro výpočet objemu V_j jehlanu potřebujeme znát obsah podstavy S_p a jeho výšku v_t = 8,55 m.
- Obsah podstavy S_p ve tvaru pentagramu (obr. 4.6.9) vypočítáme tak, že od obsahu S_1 konvexního pravidelného pětiúhelníku KLMNO odečteme pětinásobek obsahu rovnoramenného \triangle LMA o základně a = 5 m a ramenech b; S_p = S_1 - 5 \cdot S_{\triangle LMA}. Je třeba vypočítat S_{\triangle LMA}.
- Vyjádříme S_{\triangle LMA} = \frac{a v_a}{2}. Je třeba vypočítat v_a.
- Z pravoúhlého \triangle S_{LM}MA pomocí Pýthagorovy věty vyjádříme délku v_a;
v_a = \sqrt{|AM|^2 - |S_{LM}M|^2} = \sqrt{b^2 - (\frac{a}{2})^2}. Je třeba vypočítat |AM| = b. - Přepona |AM| = b pravoúhlého \triangle S_{LM}MA je zárověň ramenem rovnoramenného \triangle LMA; a také část úhlopříčky KM konvexního pravidelného pětiúhelníku KLMNO. Úhlopříčky konvexního pravidelného pětiúhelníku jsou všechny stejně dlouhé a každé dvě se vzájemně dělí v poměru \varphi nazývaném zlatý řez; číslo \varphi je zlatým číslem; \varphi = \frac {1 + \sqrt {5}}{2}.
V tomto případě se úhlopříčky KM, NL konvexního pravidelného pětiúhelníku KLMNO protínají v bodě A. Tedy pomocí zlatého řezu vyjádříme poměr mezi úsečkami: \frac{|KM|}{|KA|} = \frac{|KA|}{|AM|} = \varphi = \frac {1 + \sqrt {5}}{2}. Vyjádříme délku úsečky |KA| = a = 5 m, jelikož \triangle KAN \sim \triangle KNO a tvoří kosočtverec KANO; |KA| = a.
Ze vztahu \frac{|KA|}{|AM|} = \varphi vyjádříme |AM| = b; |AM| = \frac{|KA|}{\varphi}, tedy |AM| = \frac{a}{\varphi} = \frac{5}{\frac {1 + \sqrt {5}}{2}} m \doteq 3,090 m. - Vypočítáme v_a; v_a = \sqrt{b^2 - (\frac{a}{2})^2} = \sqrt{3,090^2 - (\frac{5}{2})^2} m \doteq 1,816 m.
- Obsah \triangle LMA je S_{\triangle LMA} = \frac{a v_a}{2} = \frac{5\ \cdot\ 1,816}{2} m = 4,540 m^2.
- Vypočítáme obsah S_1 konvexního pravidelného pětiúhelníku KLMNO o straně a = 5 m. Pravidelný pětiúhelník rozložíme na pět shodných rovnoramenných trojúhelníků; S_{\triangle LMP_{v_t}} = \frac{a\ \cdot\ |P_{v_t}S_{LM}|}{2}.
Z \triangle P_{v_t}S_{LM}M vyjádříme výšku |P_{v_t}S_{LM}|; |P_{v_t}S_{LM}| = \cot 36° \cdot \frac {a}{2} \doteq 1,376 \cdot 2,5 m \doteq 3,441 m.
Tedy S_{\triangle LMP_{v_t}} = \frac{5\ \cdot\ 3,441}{2} m^2 \doteq 8,606 m^2. Tedy S_1 = 5 \cdot S_{\triangle LMP_{v_t}} = 5 \cdot 8,606 m^2 = 43,030 m^2. - Pro obsah podstavy platí S_p = S_1 - 5 \cdot S_{\triangle LMA} = 43,030 m^2 - 5 \cdot 4,540 m^2 = 20,330 m^2.
- Pro objem jehlanu platí V_j = \frac{1}{3}S_pv_t = \frac{1}{3} \cdot 20,330 \cdot 8,55 m^3 \doteq 57,94 m^3.
- Objem nekonvexního desetibokého jehlanu KELAMBNCODV je 57,94 m^3.
