Povrch jehlanu
Tak jako u povrchu tělesa je i povrch jehlanu roven součtu obsahů všech jeho stěn, tedy obsahu jeho sítě (obr. 4.7.1). Síť jehlanu je tvořena jednou podstavou a jeho pláštěm (obr. 4.7.2).
Povrch S jehlanu je součtem obsahu jeho podstavy S_p a obsahu jeho bočních stěn, tj. pláště S_{pl}; tedy platí
S = S_p+S_{pl}.
Obrázek 4.7.1: Applet – síť nepravidelného čtyřbokého jehlanu
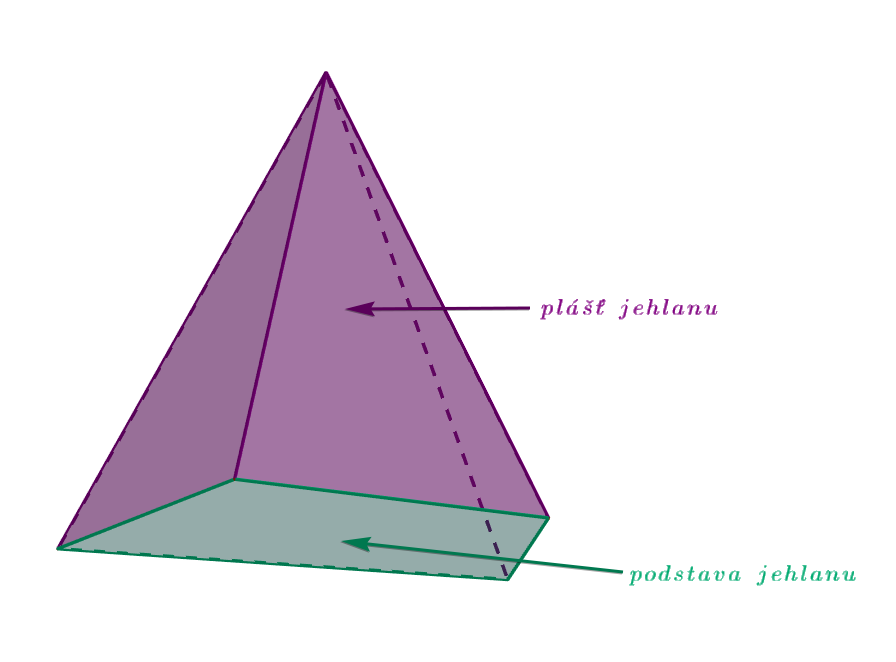
Obrázek 4.7.2: Plášť a podstava nepravidelného čtyřbokého jehlanu zobrazeného v levém podhledu
Nyní vypočítáme povrch jehlanu z Příkladu 4.6.1.
Příklad 4.7.1
Vypočítejte povrch S pravidelného čtyřbokého jehlanu ABCDV. Jeho boční stěny jsou tvořené rovnostrannými trojúhelníky o straně délky a = 5 cm, bod T je středem jeho podstavy. Výsledek zaokrouhlete na jedno desetinné místo.
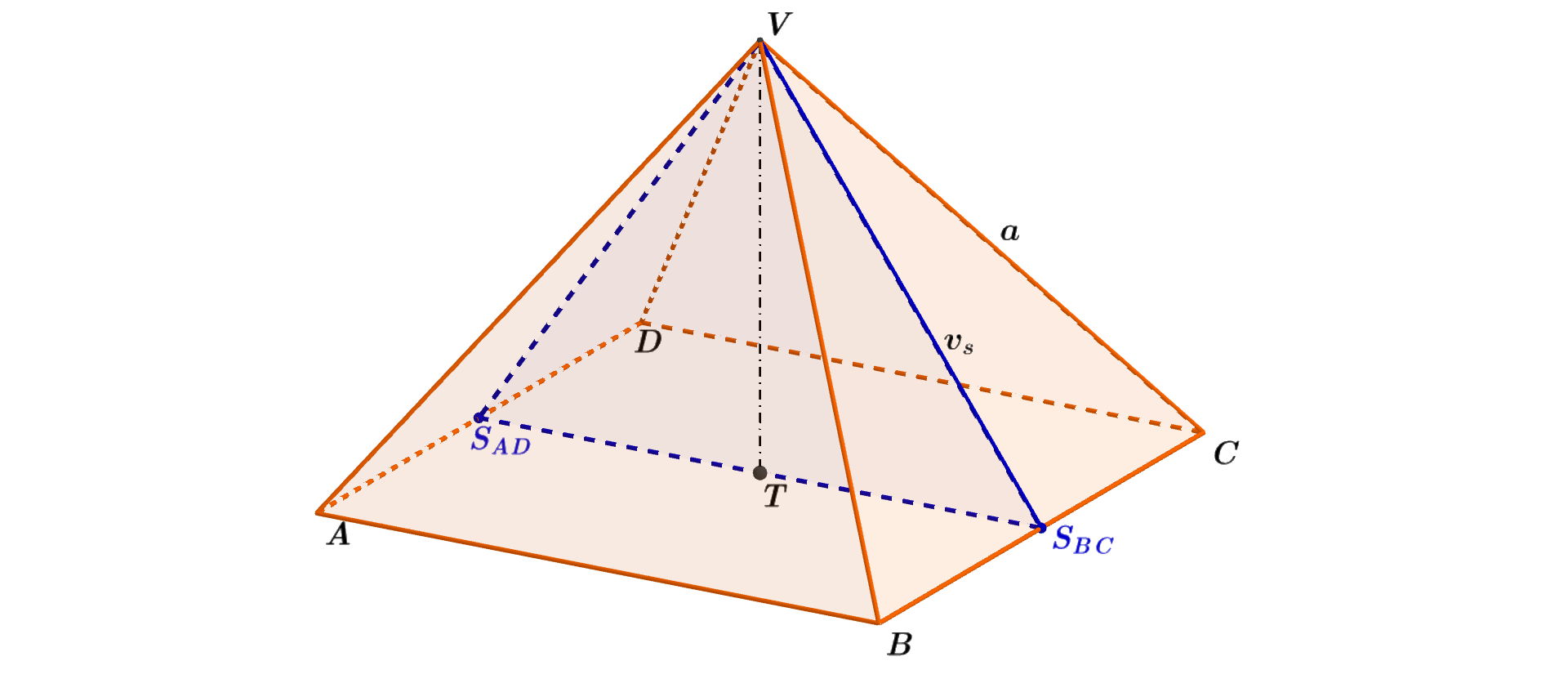
Obrázek 4.7.3: Ilustrace Příkladu 4.7.1
Řešení
- Pro výpočet povrchu jehlanu potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Jsou-li boční stěny pravidelného čtyřbokého jehlanu navzájem shodné rovnostranné trojúhelníky, tak podstava jehlanu ABCD je čtverec se stranou délky a=5 cm (obr. 4.7.3).
- S_p=a^2 = 25 cm^2.
- Plášť jehlanu je tvořen čtyřmi shodnými rovnostrannými \triangle ABV, \triangle BCV, \triangle CDV a \triangle DAV. Určíme obsah \triangle BCV.
- Pro obsah tohoto trojúhelníku platí S = \frac{a v_a}{2}, kde a je délka základny a v_a je výška k základně. Tedy a=5 cm; v_a = v_s, kde v_s je stěnová výška jehlanu. Tu jsme již určili v příkladu 3.6.1, tj. v_s=a\frac{\sqrt3}{2}.
- Obsah \triangle BCV je S_{\triangle BCV} = \frac{a v_a}{2} = \frac{a v_s}{2} = \frac{25\frac{\sqrt3}{2}}{2} cm^2 = {25\frac{\sqrt3}{4}} cm^2.
- Pro obsah pláště jehlanu platí S_{pl} = 4S_{\triangle BCV} = 25 \sqrt3 cm^2 \doteq 43,30 cm^2.
- Pro povrch S jehlanu platí S = S_p+S_{pl} = 25 cm^2 + 43,30 cm^2 \doteq 68,3 cm^2.
- Povrch pravidelného čtyřbokého jehlanu ABCDV je po zaokrouhlení 68,3 cm^2.
Nyní vypočítáme povrch jehlanu z Příkladu 4.6.2.
Příklad 4.7.2
Vypočítejte povrch S pravidelného čtyřbokého jehlanu ABCDV. Jeho boční stěny jsou tvořené shodnými rovnoramennými trojúhelníky se základnami délky a = 4 \sqrt6 cm a rameny délky q = 7 cm. Výsledek zaokrouhlete na dvě desetinná místa.
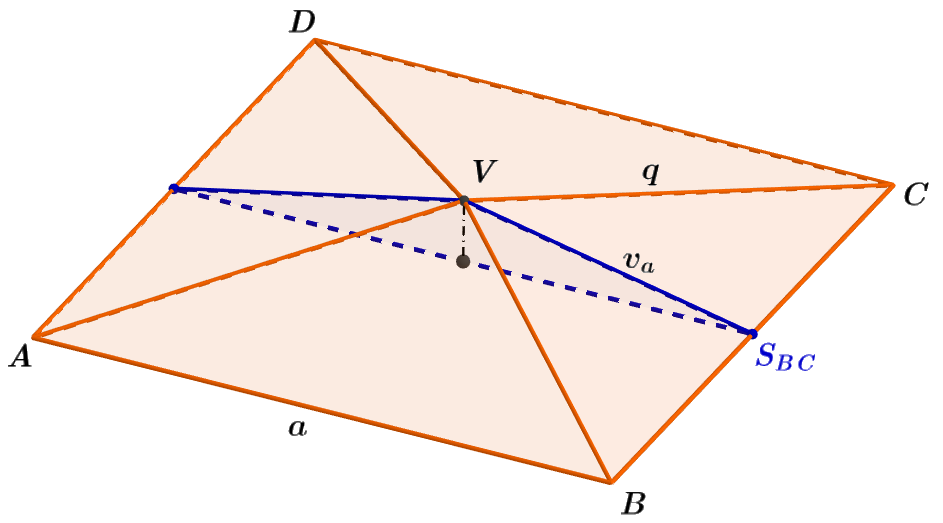
Obrázek 4.7.4: Ilustrace Příkladu 4.7.2
Řešení
- Pro výpočet povrchu jehlanu potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Jsou-li boční stěny pravidelného čtyřbokého jehlanu tvořeny rovnoramennými trojúhelníky se základnou délky a = 4 \sqrt6 cm a rameny délky q = 7 cm, tak podstava jehlanu ABCD je čtverec o straně délky a.
- S_p=a^2=(4 \sqrt6)^2 cm^2 = 96 cm^2.
- Plášť jehlanu je tvořen čtyřmi shodnými rovnoramennými \triangle ABV, \triangle BCV, \triangle CDV a \triangle DAV. Určíme obsah \triangle BCV.
- Pro obsah S trojúhelníku platí S = \frac{a v_a}{2}, kde a je délka základny a v_a je výška k základně.
Tedy a=4 \sqrt6 cm. Z pravoúhlého \triangle S_{BC}CV pomocí Pýthagorovy věty určíme v_a;
v_a = \sqrt {q^2 - (\frac{a}{2})^2 } = \sqrt {7^2 - (\frac{4\sqrt6}{2})^2} cm= \sqrt {25} cm= 5 cm. - Obsah boční stěny BCV je dán vztahem S_{\triangle BCV} = \frac{a v_a}{2} = 10\sqrt6 cm^2.
- Pro obsah pláště jehlanu platí S_{pl} = 4S_{\triangle BCV} = 40\sqrt6 cm^2 = \doteq 97,979 cm^2.
- Pro povrch jehlanu platí S = S_p+S_{pl} = 96 cm^2 + 97,979 cm^2 \doteq 193,98 cm^2.
- Povrch pravidelného čtyřbokého jehlanu ABCDV je po zaokrouhlení 193,98 cm^2.
Nyní vypočítáme povrch jehlanu z Příkladu 4.6.3.
Příklad 4.7.3
Je dán čtyřboký jehlan RSTUV, jehož podstavou je rovnoramenný lichoběžník o základnách délky a = 8 dm, c = 4,5 dm a dvěma rameny délky b = 4,3 dm. Pro výšku v_p lichoběžníku platí v_p = 4 dm. Pro délky stěnových výšek platí v_a = 5,3 dm, v_b = 5,8 dm, v_c = 5,4 dm. Vypočítejte povrch S tohoto jehlanu. Výsledek zaokrouhlete na dvě desetinná místa.
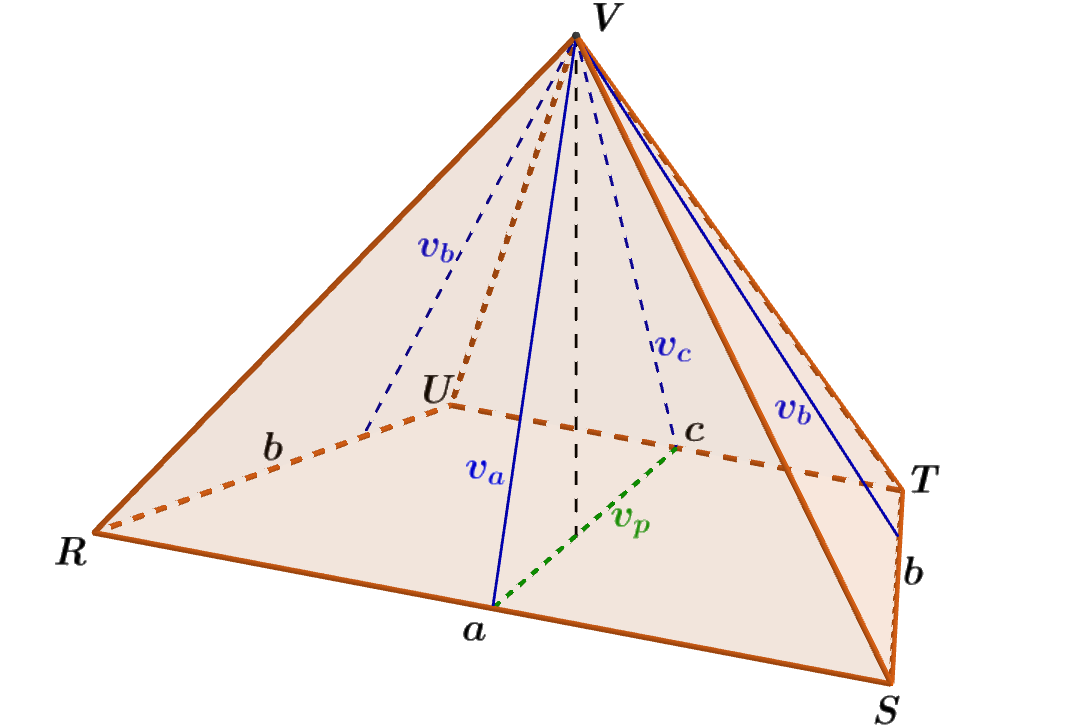
Obrázek 4.7.5: Ilustrace Příkladu 4.7.3
Řešení
- Pro výpočet povrchu jehlanu potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Pro obsah podstavy tvaru lichoběžníku platí S_p = \frac{(a\ +\ c)\ \cdot\ v_p}{2} = \frac{(8\ +\ 4,5)\ \cdot\ 4}{2} dm^2 = 25 dm^2.
- Plášť jehlanu RSTUV je tvořen čtyřmi \triangle RSV, \triangle STV, \triangle TUV a \triangle URV. Určíme obsah každého z nich.
- Pro obsah S obecného trojúhelníku platí S = \frac{a v_a}{2}, kde a je délka základny a v_a je výška k základně.
- Tedy v našem případě S_{\triangle RSV} = \frac{a v_a}{2} = \frac{8\ \cdot\ 5,3}{2} dm^2 = 21,200 dm^2. S_{\triangle STV} = S_{\triangle URV} = \frac{b v_b}{2} = \frac{4,3\ \cdot\ 5,8}{2} dm^2 = 12,470 dm^2.
- Pro obsah pláště jehlanu platí
S_{pl} = S_{\triangle RSV} + 2S_{\triangle STV} + S_{\triangle TUV} = 21, 200 dm^2 + 2 \cdot(12,470) dm^2 + 12,150 dm^2 = 58,290 dm^2. - Pro povrch jehlanu platí S = S_p+S_{pl} = 25 dm^2 + 58,290 dm^2 \doteq 83,29 dm^2.
- Povrch čtyřbokého jehlanu RSTUV je 83,29 dm^2.
S_{\triangle TUV} = \frac{c v_c}{2} = \frac{4,5\ \cdot\ 5,4}{2} dm^2 = 12,150 dm^2.
Nyní vypočítáme povrch jehlanu z Příkladu 4.6.4.
Příklad 4.7.4
Je dán pětitiboký jehlan KLMNOV, jehož podstavou je pravidelný pětiúhelník o straně a = 10 m. Pro stěnové výšky jehlanu platí v_{s_1} = 8,44 m, v_{s_2} = 10,87 m, v_{s_3} = 15,66 m, v_{s_4} = 13,69 m a v_{s_5} = 8,93 m. Určete jeho povrch S. Výsledek uveďte na dvě desetinná místa.
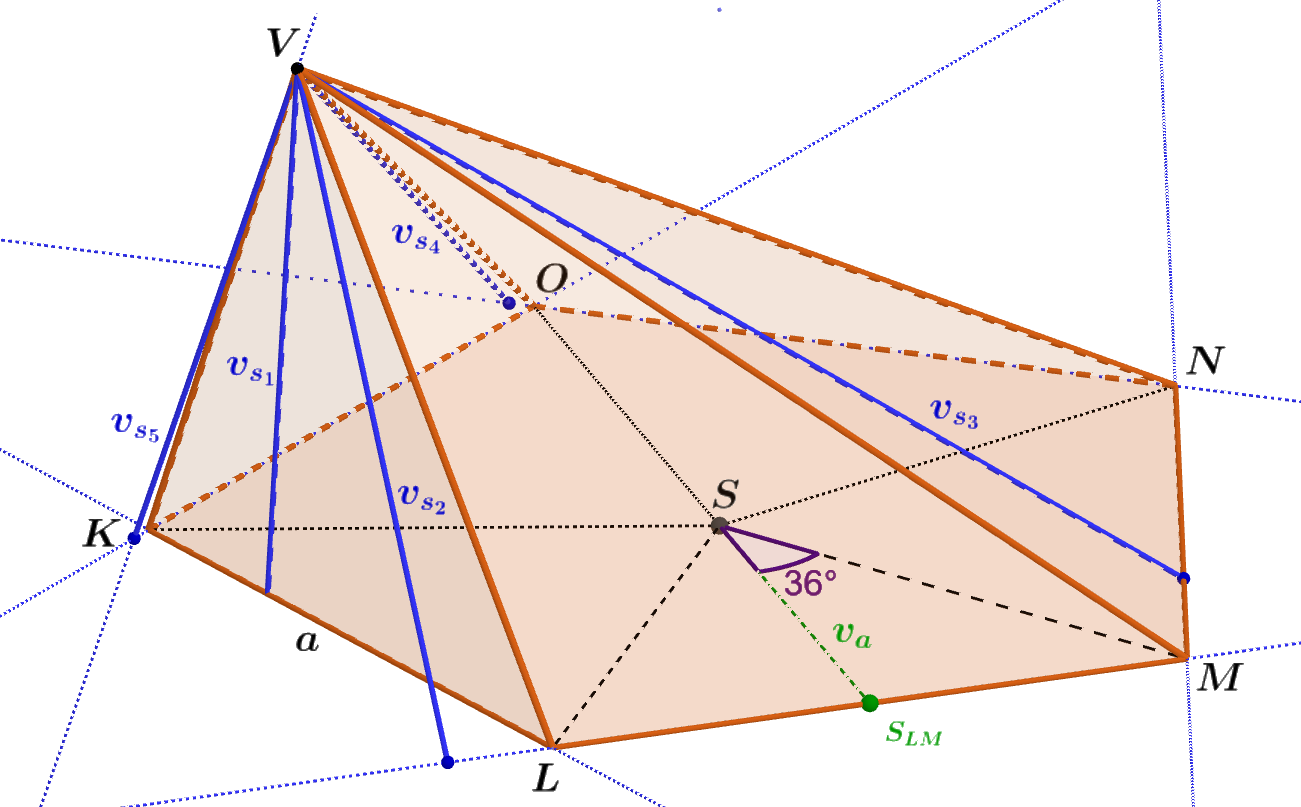
Obrázek 4.7.6: Ilustrace Příkladu 4.7.4
Řešení
- Pro výpočet povrchu S jehlanu potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Podstavou daného jehlanu je pravidelný pětiúhelník o straně a=10 m. Pravidelný pětiúhelník rozložíme na pět shodných rovnoramenných trojúhelníků (obr. 4.7.6); S_{\triangle LMS} = \frac{a v_a}{2}.
Z \triangle SS_{LM}M vyjádříme v_a; v_a = \cot 36° \cdot \frac {a}{2} \doteq 1,376 \cdot 5 m \doteq 6,882 m.
Tedy S_{\triangle LMS} = \frac{10\ \cdot\ 6,882}{2} m^2 \doteq 34,410 m^2; S_p = 5 \cdot S_{\triangle LMS} = 5 \cdot 34,410 m^2 = 172,050 m^2. - Plášť jehlanu KLMNOV je tvořen pěti různými trojúhelníky: \triangle KLV, \triangle LMV, \triangle MNV, \triangle NOV a \triangle OKV. Určíme obsah každého z nich.
- Pro obsah S obecného trojúhelníku platí S = \frac{a v_a}{2}, kde a je délka základny a v_a je výška k základně. Vypočítáme obsahy daných trojúhelníků.
- Tedy v tomto případě S_{\triangle KLV} = \frac{a v_{s_1}}{2} = \frac{10\ \cdot\ 8,44}{2} m^2 = 42,200 m^2.
S_{\triangle KLV} = \frac{a v_{s_2}}{2} = \frac{10\ \cdot\ 10,87}{2} m^2 = 54,350 m^2.
S_{\triangle KLV} = \frac{a v_{s_3}}{2} = \frac{10\ \cdot\ 15,66}{2} m^2 = 78,300 m^2.
S_{\triangle KLV} = \frac{a v_{s_4}}{2} = \frac{10\ \cdot\ 13,69}{2} m^2 = 68,450 m^2.
S_{\triangle KLV} = \frac{a v_{s_5}}{2} = \frac{10\ \cdot\ 8,93}{2} m^2 = 44,650 m^2. - Pro obsah pláště jehlanu platí
S_{pl} = S_{\triangle KLV} + 2S_{\triangle LMV} + S_{\triangle MNV} + S_{\triangle NOV} + S_{\triangle OKV} = 42,200 m^2 + 54,350 m^2 + 78,300 m^2 + 68,450 m^2 + 44,650 m^2 = 287,950 m^2. - Pro povrch jehlanu platí S = S_p+S_{pl} = 172,050 m^2 + 287,950 m^2 \doteq 460,00 m^2.
- Povrch pětibokého jehlanu KLMNO je 460,00 m^2.
Nyní vypočítáme povrch jehlanu z Příkladu 4.6.5.
Příklad 4.6.5
Je dán nekonvexní desetiboký jehlan KELAMBNCODV, jehož podstavou je pentagram – pěticípý nekonvexní hvězdicovitý mnohoúhelník, který má všechny strany stejně dlouhé, vzniklý z pravidelného konvexního pětiúhelníku o straně a = 5 m. Stěnová výška v_b jehlanu je 8,52 m. Určete jeho povrch S. Výsledek zaokrouhlete na dvě desetinná místa.
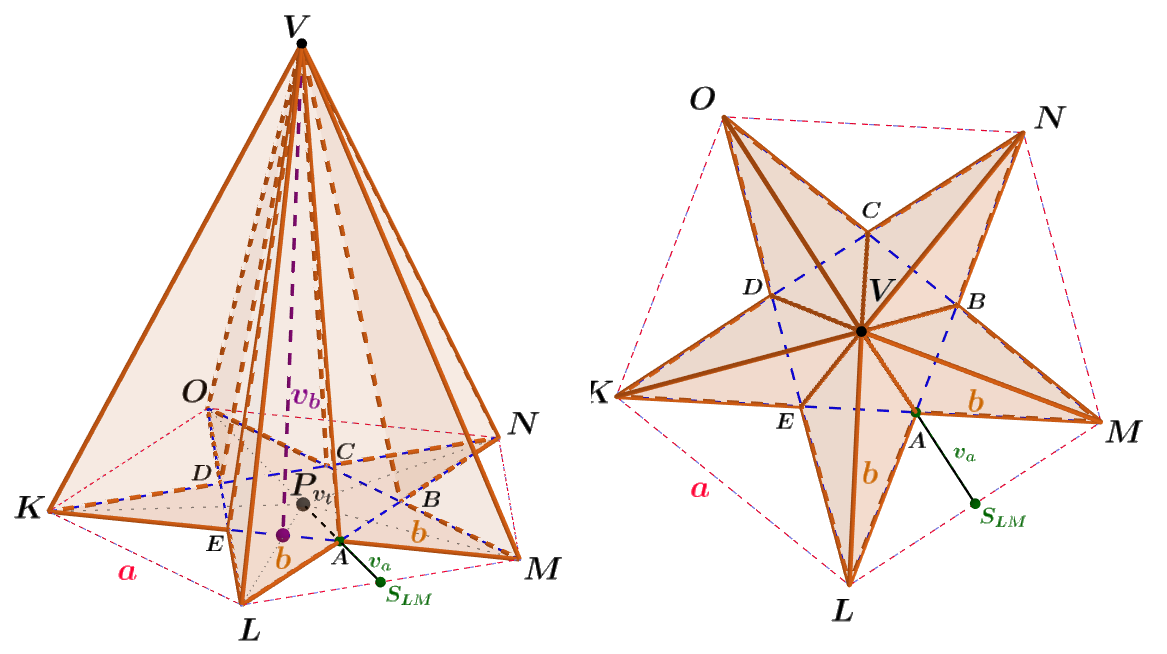
Obrázek 4.7.7: Ilustrace Příkladu 4.7.5
Řešení
- Pro výpočet objemu V_j jehlanu potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Obsah podstavy S_p ve tvaru pentagramu (obr. 4.6.9) vypočítáme tak, že od obsahu S_1 konvexního pravidelného pětiúhelníku KLMNO odečteme pětinásobek obsahu rovnoramenného \triangle LMA o základně a = 5 m a ramenech b; S_p = S_1 - 5 \cdot S_{\triangle LMA}. Je třeba vypočítat S_{\triangle LMA}.
- Vyjádříme S_{\triangle LMA} = \frac{a v_a}{2}. Je třeba vypočítat v_a.
- Z pravoúhlého \triangle S_{LM}MA pomocí Pýthagorovy věty vyjádříme délku v_a;
v_a = \sqrt{|AM|^2 - |S_{LM}M|^2)} = \sqrt{b^2 - (\frac{a}{2})^2)}. Je třeba vypočítat |AM| = b. - Přepona |AM| = b pravoúhlého \triangle S_{LM}MA je zárověň ramenem rovnoramenného \triangle LMA; a také část úhlopříčky KM konvexního pravidelného pětiúhelníku KLMNO. Úhlopříčky konvexního pravidelného pětiúhelníku jsou všechny stejně dlouhé a každé dvě se vzájemně dělí v poměru \varphi nazývaném zlatý řez; číslo \varphi je zlatým číslem; \varphi = \frac {1 + \sqrt {5}}{2}.
V tomto případě se úhlopříčky KM, NL konvexního pravidelného pětiúhelníku KLMNO protínají v bodě A. Tedy pomocí zlatého řezu vyjádříme poměr mezi úsečkami: \frac{|KM|}{|KA|} = \frac{|KA|}{|AM|} = \varphi = \frac {1 + \sqrt {5}}{2}. Vyjádříme délku úsečky |KA| = a = 5 m, jelikož \triangle KAN \cong \triangle NOK a tvoří kosočtverec KANO; |KA| = a.
Ze vztahu \frac{|KA|}{|AM|} = \varphi vyjádříme |AM| = b; |AM| = \frac{|KA|}{\varphi}, tedy |AM| = \frac{a}{\varphi} = \frac{5}{\frac {1 + \sqrt {5}}{2}} m \doteq 3,090 m. - Vypočítáme v_a; v_a = \sqrt{b^2 - (\frac{a}{2})^2)} = \sqrt{3,090^2 - (\frac{5}{2})^2)} m \doteq 1,816 m.
- Obsah \triangle LMA je S_{\triangle LMA} = \frac{a v_a}{2} = \frac{5\ \cdot\ 1,816}{2} m = 4,540 m^2.
- Vypočítáme obsah S_1 konvexního pravidelného pětiúhelníku KLMNO o straně a = 5 m. Pravidelný pětiúhelník rozložíme na pět shodných rovnoramenných trojúhelníků; S_{\triangle LMP_{v_t}} = \frac{a \cdot |P_{v_t}S_{LM}|}{2}.
Z \triangle P_{v_t}S_{LM}M vyjádříme výšku |P_{v_t}S_{LM}|; |P_{v_t}S_{LM}| = \cot 36° \cdot \frac {a}{2} \doteq 1,376\ \cdot\ 2,5 m \doteq 3,441 m.
Tedy S_{\triangle LMP_{v_t}} = \frac{5\ \cdot\ 3,441}{2} m^2 \doteq 8,606 m^2. Tedy S_1 = 5 \cdot S_{\triangle LMP_{v_t}} = 5 \cdot 8,606 m^2 = 43,030 m^2. - Pro obsah podstavy platí S_p = S_1 - 5 \cdot S_{\triangle LMA} = 43,030 m^2 - 5 \cdot 4,540 m^2 = 20,330 m^2.
- Plášť daného jehlanu je tvořen deseti navzájem shodnými trojúhelníky. Pro obsah pláště platí S_{pl} = 10 \cdot S_{\triangle LAV}; S_{\triangle LAV} = \frac{b v_b}{2} = \frac{3,090\ \cdot\ 8,52}{2} m \doteq 13,163 m^2.
Tedy S_{pl} = 10 \cdot S_{\triangle LAV} = 10 \cdot 13,163 m^2 = 131,63 m^2. - Pro povrch jehlanu platí S = S_p+S_{pl} = 20,330 m^2 + 131,63 m^2 = 151,96 m^2.
- Povrch nekonvexního desetibokého jehlanu KELAMBNCODV je 151,96 m^2.
