Povrch hranolu
Tak jako u povrchu tělesa je i povrch hranolu roven součtu obsahů všech jeho stěn, tedy obsahu jeho sítě, viz obr. 3.7.1. Síť hranolu je tvořena dvěma shodnými podstavami a jeho pláštěm (obr. 3.7.2).
Povrch S hranolu je roven součtu obsahů S_p jeho dvou podstav a obsahu jeho bočních stěn, tj. pláště S_{pl}, platí:
S = 2S_p+S_{pl}.
Obrázek 3.7.1: Applet – síť šestibokého kosého hranolu
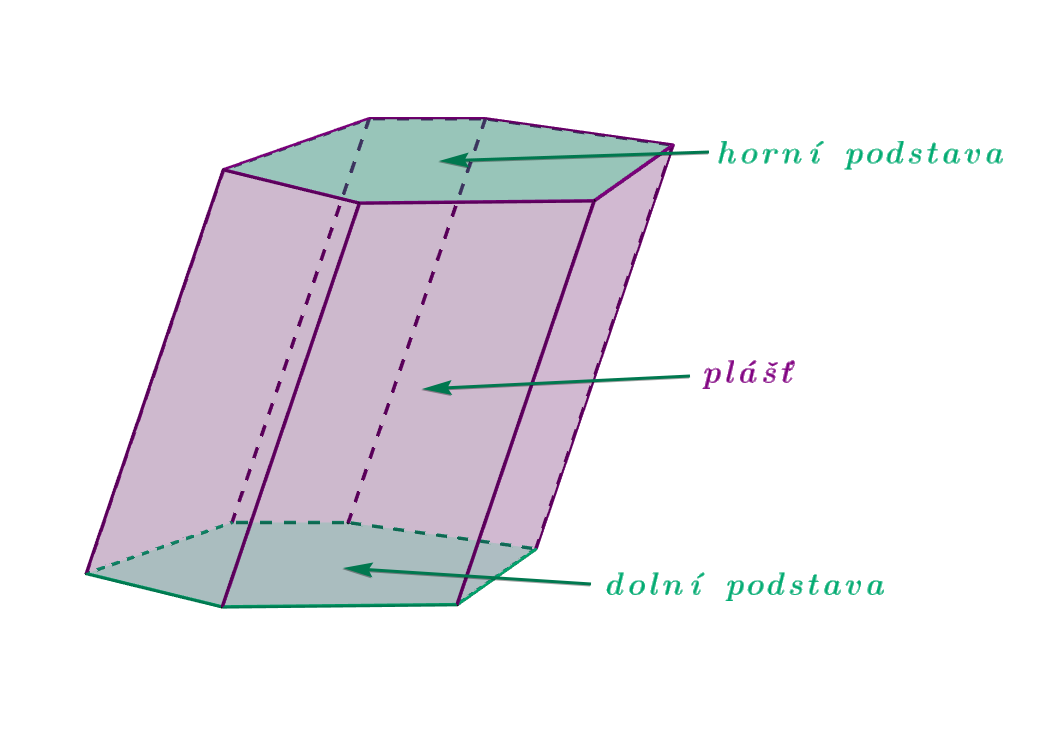
Obrázek 3.7.2: Povrch šestibokého kosého hranolu ‐ plášť a podstavy
Nyní vypočítáme povrch hranolu z Příkladu 3.6.1.
Příklad 3.7.1
Vypočítejte povrch S pravidelného pětibokého hranolu ABCDEFGHIJ. Jeho boční stěny jsou tvořeny shodnými čtverci o straně délky a = 5 cm. Bod T je těžištěm podstavy. Výsledek zaokrouhlete na dvě desetinná místa.
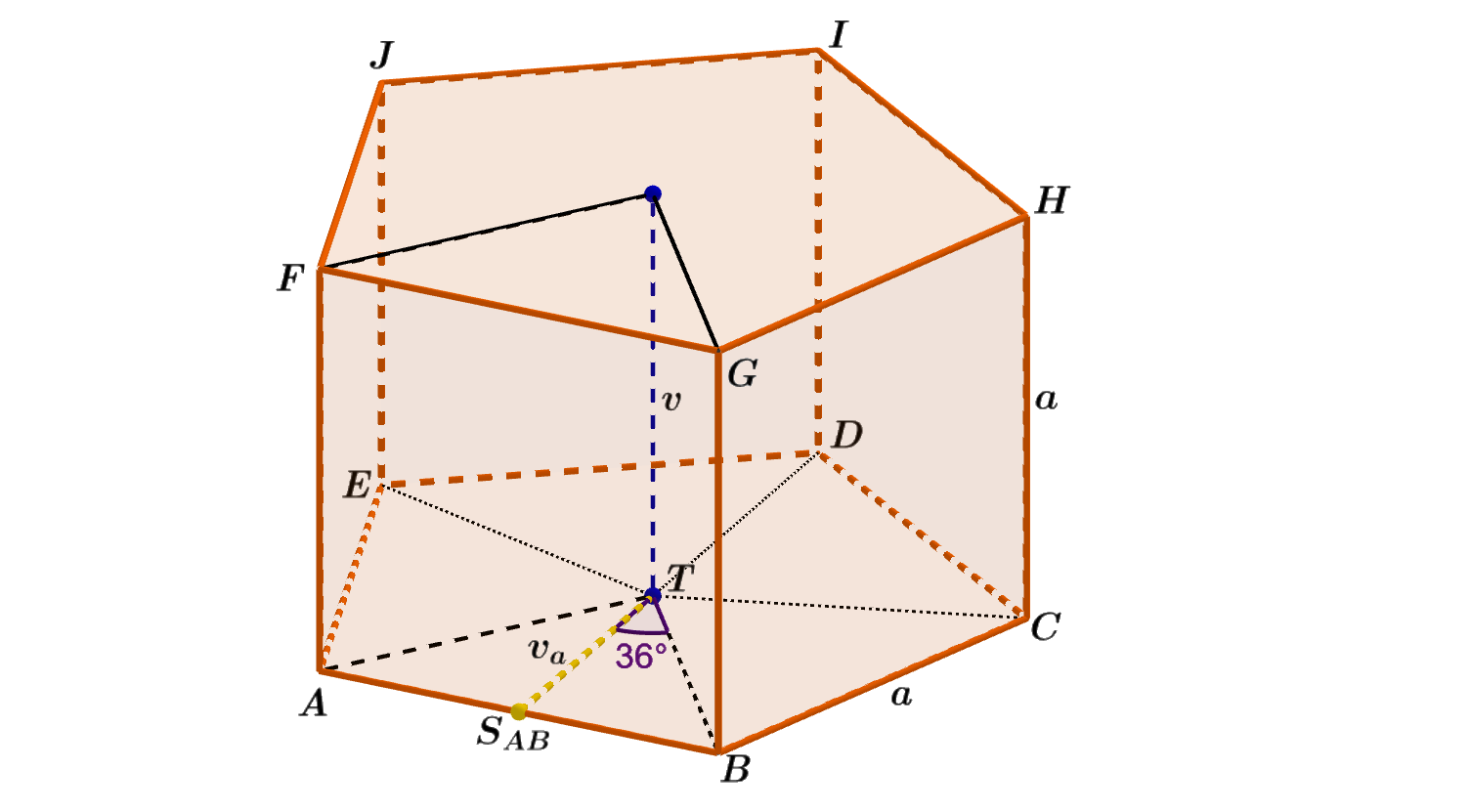
Obrázek 3.7.3: Ilustrace Příkladu 3.7.1
Řešení
- Pro povrch S hranolu platí S = 2S_p + S_{pl}, tedy potřebujeme znát obsahy podstav S_p daného hranolu a obsah jeho pláště S_{pl}.
- Podstavami hranolu ABCDEFGHIJ jsou pravidelné pětiúhelníky o straně délky a=5 cm. Pravidelný pětiúhelník rozložíme na pět shodných rovnoramenných trojúhelníků (obr. 3.7.3); S_{\triangle ABT} = \frac{a v_a}{2}.
Z \triangle AS_{AB}T vyjádříme v_a; v_a = \cot 36° \cdot \frac {a}{2} = 1,376 \cdot 2,5 cm \doteq 3,441 cm.
Tedy S_{\triangle ABT} = \frac{5\ \cdot\ 3,441}{2} cm^2 \doteq 8,603 cm^2. - Pro obsah podstavy S_p platí: S_p = 5 \cdot S_{\triangle AS_{AB}T} = 5 \cdot 8,603 cm^2 \doteq 43,015 cm^2.
- Pro určení obsahu pláště S_{pl} hranolu, si uvědomíme, že jeho plášť je tvořen pěti shodnými čtverci o straně délky a=5 cm: ABGF, BCHG, CDIH, DEJI, EAFJ. Určíme obsah čtverce ABFG.
- S_{ABFG} = a^2 = 25 cm^2; S_{pl} = 5 \cdot S_{ABFG} = 125 cm^2.
- Pro povrch hranolu platí S = 2S_p+S_{pl} = 2\cdot 43,015 cm^2 + 125 cm^2 \doteq 211,03 cm^2.
- Povrch pravidelného pětibokého hranolu ABCDEFGHIJ je po zaokrouhlení 211,03 cm^2.
Nyní vypočítáme povrch hranolu z Příkladu 3.6.2.
Příklad 3.7.2
Je dán kosý šestiboký hranol GHIJKLMNOPQR, jehož podstavy jsou pravidelné šestiúhelníky o straně a = 4 dm. Jeho tělesová výška v_t = 6 dm. Výška v_1 kosodélníku LGMR je 6,11 dm. Výška v_2 kosodélníku GHNM je 7,23 dm. Výška v_3 kosodélníku HION je 7,95 dm. Jaký je povrch S tohoto hranolu? Výsledek zaokrouhlete na dvě desetinná místa.
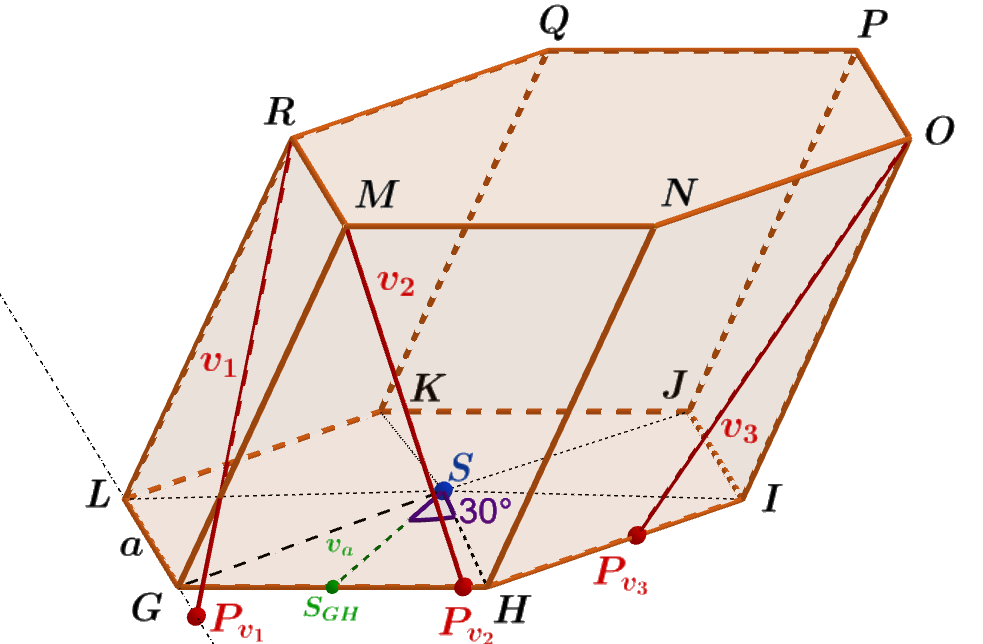
Obrázek 3.7.6: Ilustrace Příkladu 3.7.2
Řešení
- Pro povrch S hranolu platí S = 2S_p + S_{pl}, tedy potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Podstavami hranolu GHIJKLMNOPQR jsou pravidelné šestiúhelníky o straně délky a=6 dm (obr. 3.7.6). Pravidelný šestiúhelník rozložíme na šest shodných rovnostranných trojúhelníků; S_{\triangle GHS} = \frac{a v_a}{2}. Z \triangle S_{GH}HS vyjádříme v_a; v_a = \cot 30° \cdot \frac {a}{2} = 1,732 \cdot 2 dm \doteq 3,464 dm. Tedy S_{\triangle GHS} = \frac{4\ \cdot\ 3,464}{2} dm^2 \doteq 6,928 dm^2.
- Pro obsah podstavy S_p platí: S_p = 6 \cdot S_{\triangle GHS} = 6 \cdot 6,928 dm^2 \doteq 41,892 dm^2.
- Plášť hranolu je tvořen třemi dvojicemi navzájem shodných kosodélníků S_{pl} = 2 \cdot S_{LGMR} + 2 \cdot S_{GHNM} + 2 \cdot S_{HION}.
- Výška v_1 kosodélníku LGMR je rovna výšce kosodélníku IJPO; v_1 = 6,11 dm. Výška v_2 kosodélníku GHNM je rovna výšce kosodélníku JKQP; v_2 = 7,23 dm. Výška v_3 kosodélníku HION je rovna výšce kosodélníku KLRQ; v_3 = 7,95 dm.
- Vypočítáme obsahy jednotlivých stěn – kosodélníků; S_{LGMR} = a \cdot v_1 = 4 \cdot 6,11 dm^2 = 24,440 dm^2,
S_{LGMR} = a \cdot v_2 = 4 \cdot 7,23 dm^2 = 28,920 dm^2,
S_{LGMR} = a \cdot v_3 = 4 \cdot 7,95 dm^2 = 31,800 dm^2. - Dosadíme hodnoty; S_{pl} = 2 \cdot S_{LGMR} + 2 \cdot S_{GHNM} + 2 \cdot S_{HION} =
= 2 \cdot 24,440 dm^2 + 2 \cdot 28,920 dm^2 + 2 \cdot 31,800 dm^2 = 170,320 dm^2. - Pro povrch hranolu platí S = 2S_p + S_{pl} = 2 \cdot 41,892 dm^2 + 170,320 dm^2 \doteq 254,10 dm^2.
- Povrch kosého šestibokého hranolu GHIJKLMNOPQR je po zaokrouhlení 254,10 dm^2.
Nyní vypočítáme povrch hranolu z Příkladu 3.6.3.
Příklad 3.7.3
Je dán kolmý čtyřboký hranol RTUVWXYZ, jehož podstavou je rovnoramenný lichoběžník o základnách délky a = 8 m, c = 4,5 a dvěma rameny délky b = 4,3 m. Výška v_p lichoběžníku je 4 m a pro délku tělesové výšky platí v_t = 5 m. Vypočítejte povrch S tohoto hranolu. Výsledek uveďte na jedno desetinné místo.
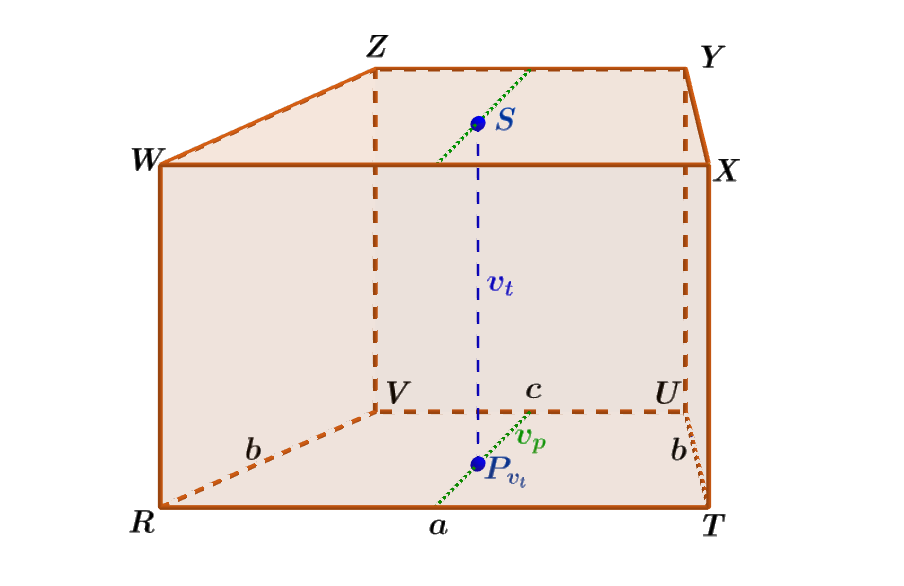
Obrázek 3.7.8: Ilustrace Příkladu 3.7.3
Řešení
- Pro povrch S hranolu platí S = 2S_p + S_{pl}, tedy potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Podstavami hranolu RTUVWXYZ jsou shodné rovnoramenné lichoběžníky o ramenech délky a = 8 m, c = 4,5 m (obr. 3.7.8). Vypočítáme obsah S_p jedné podstavy, tedy obsah rovnoramenného lichoběžníku; S_p = S_{RTUV} = \frac{(a\ +\ c)\ \cdot\ v_p}{2} = \frac{(8\ +\ 4,5)\ \cdot\ 4}{2} m^2 = 25 m^2.
- Plášť hranolu je tvořen čtyřmi obdélníky, a to RTXW, VUYZ a jednou dvojicí navzájem shodných obdélníků RVZW, TUYX.
- Vypočítáme obsahy jednotlivých stěn – obdélníků; S_{RTXW} = a \cdot v_t = 8 \cdot 5 m^2 = 40 m^2,
S_{VUYZ} = c \cdot v_t = 4,5 \cdot 5 m^2 = 22,50 m^2,
S_{RVZW} = b\cdot v_t = 4,3 \cdot 5 m^2 = 21,50 m^2. - Dosadíme; S_{pl} = S_{RTXW} + S_{VUYZ} + 2 \cdot S_{RVZW} =
= 40 m^2 + 22,50 m^2 + 2 \cdot 21,50 m^2 = 105,50 m^2. - Pro povrch hranolu platí S = 2S_p + S_{pl} = 2 \cdot 25 m^2 + 105,50 m^2 \doteq 155,5 m^2.
- Povrch kolmého čtyřbokého hranolu RTUVWXYZ je 155,5 m^3.
Nyní vypočítáme povrch hranolu z Příkladu 3.6.4.
Příklad 3.7.4
Vyjádřete povrch nekonvexního kolmého pětibokého hranolu A_1A_2S_1A_3A_4A_5A_6S_2A_7A_8, který vznikl z pravidelného čtyřbokého hranolu A_1A_2A_3A_4A_5A_6A_7A_8 o podstavné hraně a a výšce v odseknutím kolmého trojbokého hranolu o stejné výšce v, jehož dolní podstavou je \triangle A_2S_1A_3, kde S_1 je střed čtvercové podstavy A_1A_2A_3A_4.
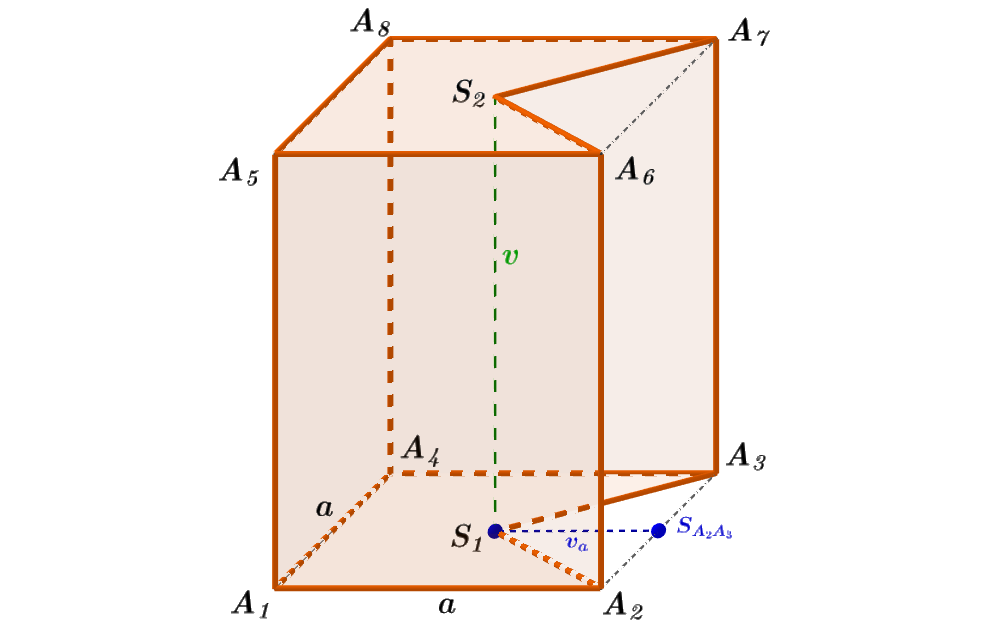
Obrázek 3.7.9: Ilustrace Příkladu 3.7.4
Řešení
- Pro povrch S hranolu platí S = 2S_p + S_{pl}, tedy potřebujeme znát obsah podstavy S_p a obsah jeho pláště S_{pl}.
- Podstavami hranolu A_1A_2S_1A_3A_4A_5A_6S_2A_7A_8 jsou nekonvexní pětiúhelníky vzniklé ze čtverce A_1A_2A_3A_4 odseknutím rovnoramenného \triangle A_2S_1A_3 s výškou v_a = \frac {a}{2} (obr. 3.7.9). Vyjádříme obsah S_p jedné podstavy, tedy obsah nekonvexního pětiúhelníku A_1A_2S_1A_3A_4;
S_p = a^2 - \frac{a\ \cdot\ v_a}{2} = a^2 - \frac{a\ \cdot\ \frac{a}{2}}{2} = a^2 - \frac{a^2}{4} = \frac{3a^2}{4}. - Plášť hranolu je tvořen jednou trojicí navzájem shodných obdélníků A_1A_2A_6A_5, A_3A_4A_8A_7, A_4A_1A_5A_8 a jednou dvojicí navzájem shodných obdélníků A_2S_1S_2A_6, S_1A_3A_7S_2.
- Vyjádříme obsahy jednotlivých stěn – obdélníků; S_{A_1A_2A_6A_5} = av, S_{A_2S_1S_2A_6} = |A_2S_1| \cdot v, kde Pýthagorovou větou vyjádříme délku úsečky A_2S_1;
|A_2S_1| = \sqrt {(\frac {a}{2})^2 + (v_a)^2} = \sqrt {(\frac {a}{2})^2 + (\frac {a}{2})^2} = \sqrt {2 \frac {a^2}{4}} = \sqrt {2} \cdot \frac {a}{2}. Tedy S_{A_2S_1S_2A_6} = \sqrt {2} \cdot \frac {a}{2} \cdot v = \frac {\sqrt {2}av}{2}.
- Dosadíme; S_{pl} = 3 \cdot S_{A_1A_2A_6A_5} + 2 \cdot S_{A_2S_1S_2A_6} = 3 \cdot av + 2 \cdot \frac {\sqrt {2}av}{2} = 3av + \sqrt {2} av = av \cdot (3 + \sqrt {2}).
- Pro povrch hranolu platí
S = 2S_p + S_{pl} = 2 \cdot \frac{3a^2}{4} + av \cdot (3 + \sqrt {2}) = \frac{3a^2}{2} + av \cdot (3 + \sqrt {2}) = a \cdot (\frac{3a}{2} + v \cdot (3 + \sqrt {2})). - Povrch nekonvexního kolmého pětibokého hranolu A_1A_2S_1A_3A_4A_5A_6S_2A_7A_8 je a \cdot (\frac{3a}{2} + v \cdot (3 + \sqrt {2})).
