Mnohostěn
Připomeneme si pojem mnohoúhelníku, který známe z planimetrie [5, s. 122].
Kromě obecného mnohoúhelníku zavádíme také pravidelný mnohoúhelník.
Mnohoúhelníky také nazýváme n-úhelníky, kde n \in \mathbb{N} udává počet vrcholů mnohoúhelníku. Z definice pravidelného mnohoúhelníku vyplývá, že nemůžeme mezi ně řadit například nekonvexní hvězdicovité mnohoúhleníky (obr. 2.2.1).

Obrázek 2.2.1: Nekonvexní hvězdicovité mnohoúhelníky (pěticípý, šesticípý a sedmicípý)
Mnohostěny v prostoru jsou analogií mnohoúhelníků v rovině. Následující zavedení mnohostěnu vychází z [5, s. 147] a z [9, s. 127].
Mnohostěn (polyedr, n-stěn) je každé těleso, jehož hranice, resp. povrch je sjednocením n mnohoúhelníků (stěn) takových, že strana každého z nich je zároveň stranou sousedního mnohoúhelníku a žádné dva sousední mnohoúhelníky neleží ve stejné rovině. Součástí mnohostěnu (jako každého tělesa) je i jeho vnitřek.
Na následujícím appletu (obr. 2.2.2) s mnohostěny se nachází nekonvexní pětiboký kolmý hranol, nepravidelný šestiboký jehlan a pravidelný dvanáctistěn.
Obrázek 2.2.2: Applet – skupina mnohostěnů v prostoru
Z definice mnohostěnu plyne, že jeho stěny tvoří mnohoúhelníky. Zavádíme následující pojmy ilustrované na obr. 2.2.3:
- Strany těchto mnohoúhelníků (průsečnice stěn) označujeme jako hrany mnohostěnu.
- Body, v nichž se hrany sbíhají (vrcholy mnohoúhelníků) jsou zároveň vrcholy mnohostěnu.
- Úsečka, která spojuje dva vrcholy mnohostěnu ležící v jedné jeho stěně a která není hranou příslušného mnohostěnu, se nazývá stěnová úhlopříčka mnohostěnu.
- Úsečka, která spojuje dva vrcholy mnohostěnu a která neleží v téže stěně, se nazývá tělesová úhlopříčka mnohostěnu.
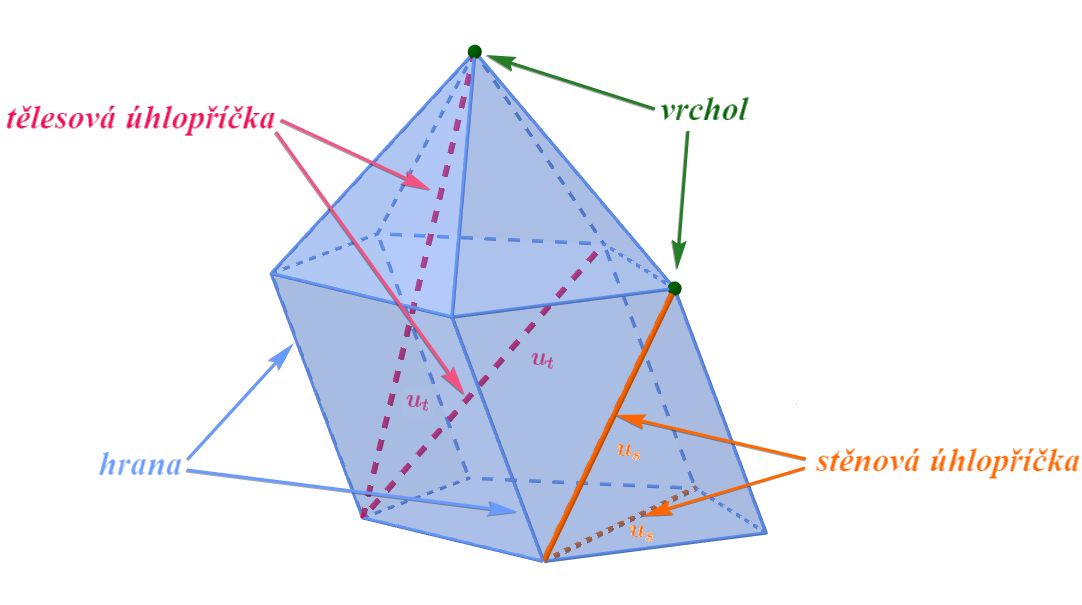
Obrázek 2.2.3: Obecný jedenáctiboký mnohostěn
Poznámka
- Stěny, které mají společnou hranu, se nazývají sousední stěny.
- Vrcholy, které leží na stejné hraně, se nazývají sousední vrcholy.
Umístěním všech stěn mnohostěnu do vhodného uskupení v jedné rovině tak, aby vznikl jeden rovinný obrazec, získáme síť mnohostěnu (obr. 2.2.4).
Poznámka
Nezapomínejme, že každá sestava všech stěn mnohostěnu síť nutně tvořit nemusí. Stěny musí být vhodně umístěny tak, aby bylo možné tuto síť složit pouhým ohýbáním papíru (v případě vyrobeného papírového modelu).
Obrázek 2.2.4: Applet – síť mnohostěnu (pravidelného dvacetistěnu)
Názvy mnohostěnů souvisí s počtem jejich stěn.
Poznámka
Mnohostěny jsou pojmenovávány podle počtu stěn (čtyři a více). Jejich cizojazyčné názvy pocházejí z řečtiny. Tedy dostáváme následující názvy mnohostěnů: čtyřstěn (tetraedr), pětistěn (pentaedr), šestistěn (hexaedr), sedmistěn (heptaedr), osmistěn (oktaedr), devítistěn (nonaedr), desetistěn (dekaedr), jedenáctistěn (undekaedr), dvanáctistěn (dodekaedr), dvacetistěn (ikosaedr) atd. Pro běžně používané mnohostěny máme samostatná označení, jako je krychle a kvádr (případy šestistěnu), jehlan apod.
Kromě obecného mnohostěnu zavádíme také pravidelný mnohostěn.
Pravidelným mnohostěnem nazýváme konvexní mnohostěn, jehož všechny stěny jsou navzájem shodné pravidelné n-úhelníky (n\ge3, n \in \mathbb{N}) a zároveň z každého vrcholu vychází stejný počet hran q (q\ge3, q \in \mathbb{N}).
Pravidelné konvexní mnohostěny nazýváme Platónovými či platónskými tělesy. Těmto tělesům se budeme věnovat v samostatné kapitole.
Poznámka
Pokud v definici pravidelného mnohostěnu vynecháme podmínku konvexnosti tělesa, tak mezi pravidelné mnohostěny můžeme zařadit i nekonvexní Kepler-Poinsotovy mnohostěny. Čtyři Kepler-Poinsotova tělesa patří do skupivy tzv. hvězdicovitých mnohostěnů, které vznikají z platónských těles. Na obr. 2.2.5 jsou vyobrazena Keplerova tělesa – malý a velký hvězdicový dvanáctistěn. Na obr. 2.2.6 jsou vyobrazena Poisontova tělesa – velký dvacetistěn a velký dvanáctistěn.
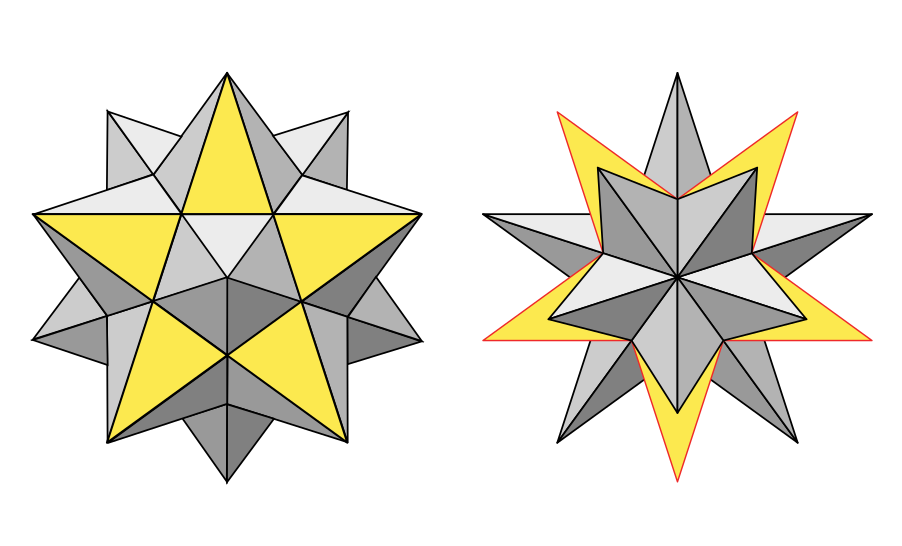
Obrázek 2.2.5: Keplerova tělesa [20]
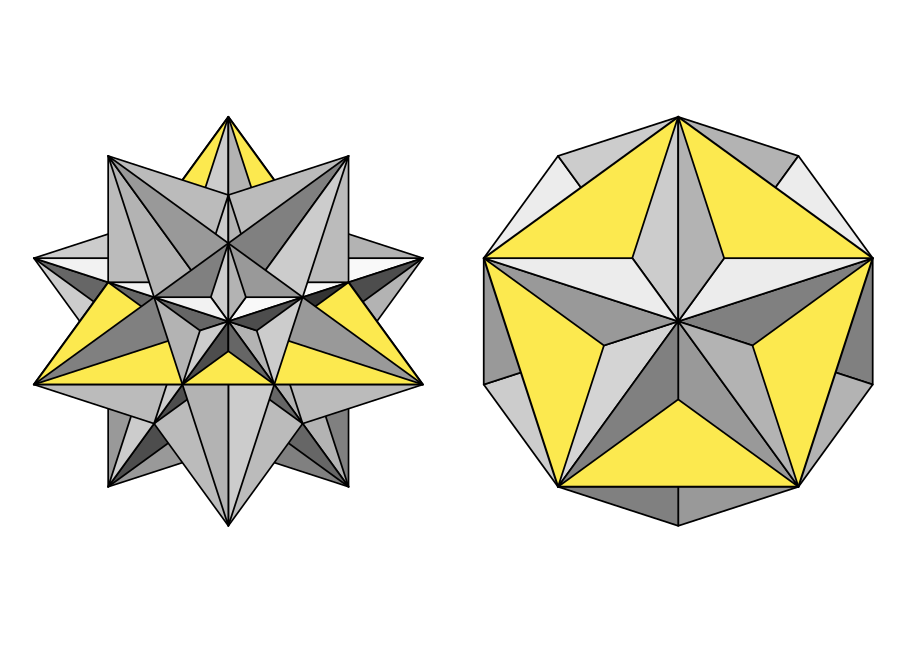
Obrázek 2.2.6: Poisontova tělesa [20]

Následující věta zvaná Eulerova věta je užitečným nástrojem pro zkoumání počtů stěn, vrcholů a hran jednotlivých konvexních mnohostěnů.
Eulerova věta
Součet počtu vrcholů a stěn konvexního mnohostěnu je roven počtu jeho hran zvětšenému o dvě.
Označíme-li s počet stěn, h počet hran, v počet vrcholů konvexního mnohostěnu, pak platí:
s+v=h+2.

Poznámka
V souladu s rámcovými vzdělávacími programy matematiky pro druhý stupeň základní školy a pro školy střední se budeme zabývat zejména mnohostěny konvexními. V této práci se z konvexních mnohostěnů zabýváme především hranoly a jehlany.
