Objem a povrch
Nejprve si položme několik otázek z různých oblastí lidské činnosti.
- Kolik čtyřicetikilových kbelíků bílé malířské barvy bude zapotřebí na jeden nátěr kancelářského komplexu, jestliže celková plocha nátěru je 1~850 m²? Vydatnost/kryvost jedné vrstvy je 8 m²/kg (obr. 2.4.2).
- V bazénu pro slony v zoologické zahradě se musí čtyřikrát měsíčně vyměnit polovina vody. Kolik korun činí měsíční náklady na vodu, jestliže cena vodného a stočného (dohromady) je 94 Kč/m³ a bazén má tvar kvádru o rozměrech 4 m, 5 m a 6 m?

Obrázek 2.4.1: Čtyřicetikilová malířská barva
K vyřešení těchto úloh potřebujeme umět určit objem a povrch těles. Tyto pojmy si nyní vysvětlíme.
Objem
Výpočet objemu tělesa lze pokládat za jedno z nejstarších využití geometrie v praktickém životě. Objem tělesa se ve školské matematice zavádí obvykle takto [9, s. 149], [5, s. 212], [7, s. 328]:
Objem V tělesa T je kladné číslo, přiřazené tělesu tak, že platí:
1. Shodná tělesa mají sobě rovné objemy.
2. Jestliže je těleso složeno z několika nepronikajících se těles, je jeho objem roven součtu objemů dílčích těles (aditivita objemu).
3. Objem krychle, jejíž hrana má délku 1 (mm, cm, m …), je roven 1 (mm³, cm³, m³ …).
Objem se značí písmenem V (počáteční písmeno latinského slova volumen znamenající právě objem).
Tedy objem V tělesa udává, jakou „část prostoru toto těleso zabírá“ ve srovnání s jednotkovou krychlí (krychle s hranou jednotkové délky). Zároveň objem V je fyzikální veličina, ke které je přiřazena číselná hodnota a jednotka. Číselná hodnota je závislá na volbě jednotky. Měřící jednotkou objemu je metr krychlový (značka m^3). Z m^3 jsou odvozeny jeho násobky nebo díly pomocí dekadických předpon (mm^3, cm^3, dm^3, km^3). Pro specializované oblasti se používají vedlejší jednotky – objem je možné také udávat v litrech (l) nebo hektolitrech (hl).
Následuje tabulka (tab. 2.4.1) převodních vztahů pro milimetr krychlový (mm³), centimetr krychlový (cm³), decimetr krychlový (dm³), metr krychlový (m³) a kilometr krychlový (km³).
| 1 mm³ | = | 0,00 1 cm³ | = | 0,000 001 dm³ | = | 0,000 000 001 m³ |
|---|---|---|---|---|---|---|
| 1 000 mm³ | = | 1 cm³ | = | 0,001 dm³ | = | 0,000 001 m³ |
| 1 000 000 mm³ | = | 1 000 cm³ | = | 1 dm³ | = | 0,001 m³ |
| 1 000 000 000 mm³ | = | 1 000 000 cm³ | = | 1 000 dm³ | = | 1 m³ |
| 1 m³ | = | 0,000 000 001 km³ | ||||
| 1 000 000 000 m³ | = | 1 km³ | ||||
Tabulka 2.4.1 – Převodní vztahy jednotek objemu
Objem se často vyjadřuje v jednotkách odvozených od litru (vedlejší jednotka).
1 l = 1 dm³
Následuje tabulka (tab. 2.4.2) převodních vztahů pro mililitr (ml), centilitr (cl), decilitr (dl), litr (l) a hektolitr (hl).
| 1 ml | = | 0,1 cl | = | 0,01 dl | = | 0,001 l |
|---|---|---|---|---|---|---|
| 10 ml | = | 1 cl | = | 0,1 dl | = | 0,01 l |
| 100 ml | = | 10 cl | = | 1 dl | = | 0,1 l |
| 1 000 ml | = | 100 cl | = | 10 dl | = | 1 l |
| 1 l | = | 0,01 hl | ||||
| 100 l | = | 1 hl | ||||
Tabulka 2.4.2 – Převodní vztahy vedlejších jednotek objemu
Poznámka
Jedna ze základních vlastností objemu tělesa (aditivní vlastnost – aditivita objemu) se využívá při určování objemů těles, která se dají rozložit na konečný počet nepronikajících se těles s objemy V_1, V_2, … ,V_n a platí:
V = V_1 + V_2 + … + V_n.
Ilustrace této vlastnosti objemu jsou na obr. 2.4.4 a obr. 2.4.5.
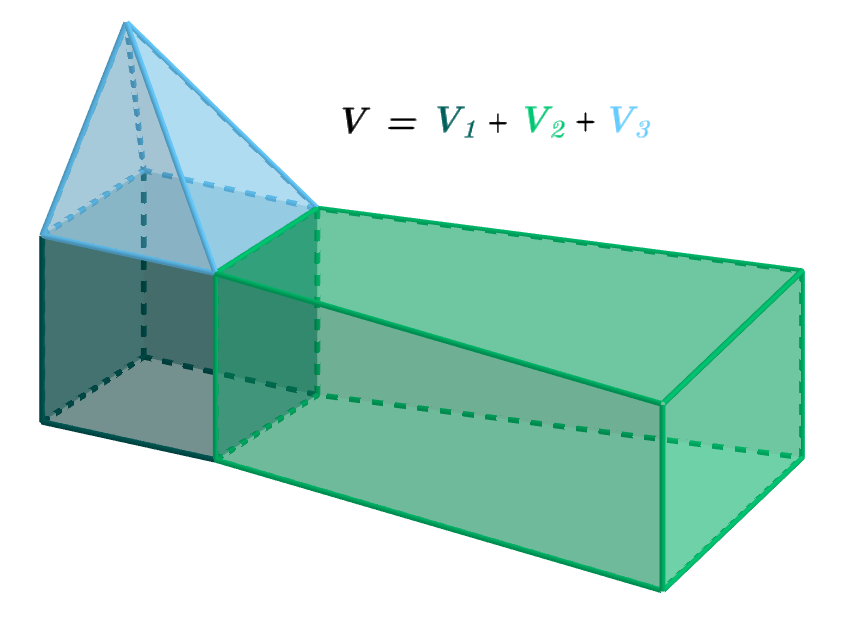
Obrázek 2.4.4: Těleso složené ze tří různých těles
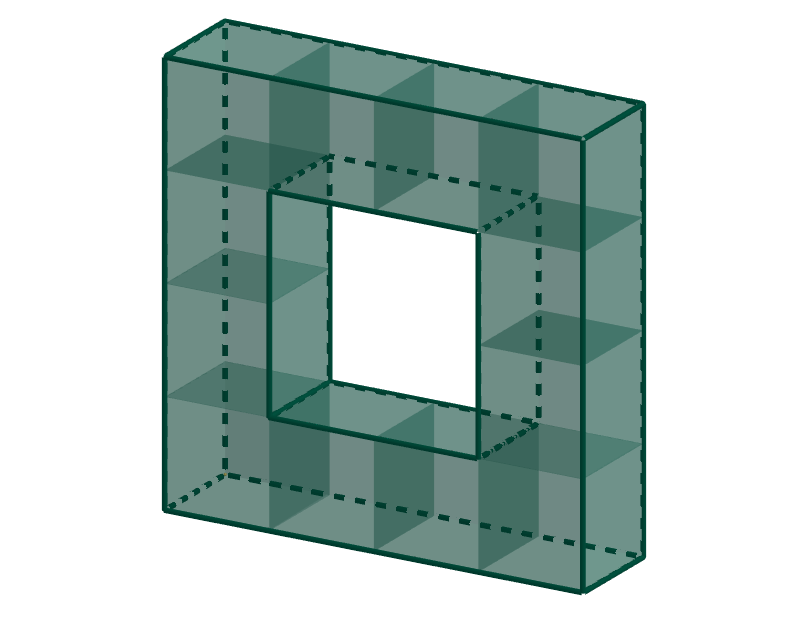
Obrázek 2.4.5: Těleso složené z dvanácti krychlí
Názorně lze určovat objem některých těles tak, že je rozložíme na konečný počet nepronikajících se jednotkových krychlí a objem tělesa je číselně roven počtu těchto krychlí. Na obr. 2.4.6 máme znázorněný kvádr s rozměry 6 cm, 5 cm a 4 cm, jehož objem je 120 cm³, neboť se dá rozložit na 120 krychliček o hraně 1 cm. Objem tohoto kvádru je dán součinem jeho tří rozměrů.
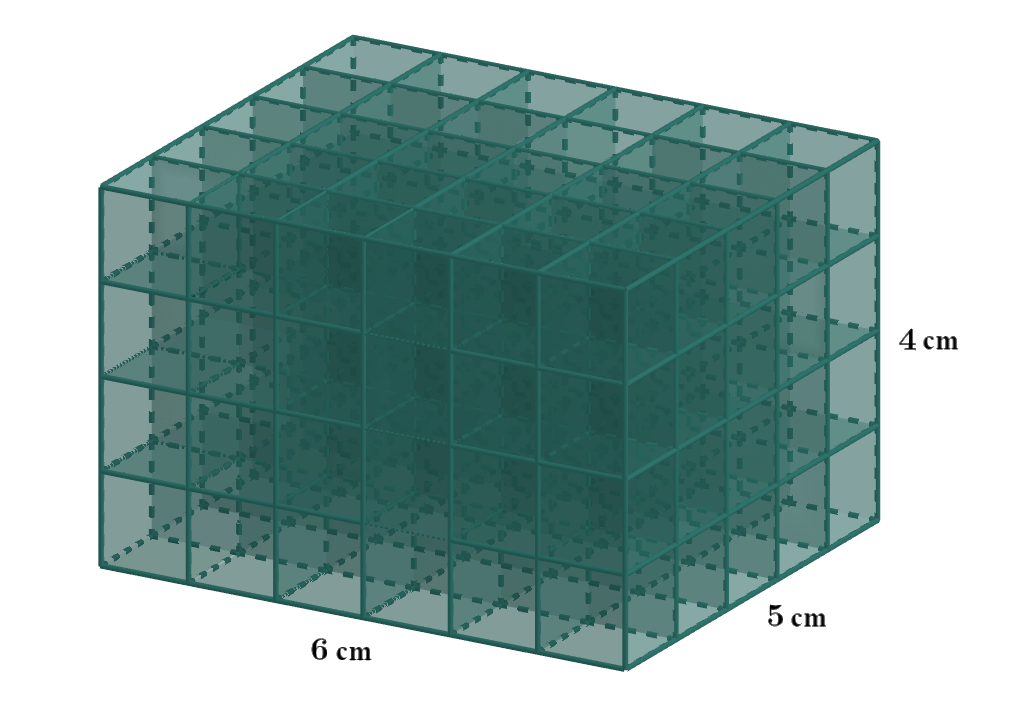
Obrázek 2.4.6: Kvádr rozložený na 120 jednotkových krychlí
Další z nástrojů pro určení objemu těles je tzv. Cavalieriho princip (viz [3, s. 263], [2a, s.119]).
Cavalieriho princip
Pokud pro dvě tělesa T_1, T_2 se stejnou výškou existují takové řezy rovinami, které jsou rovnoběžné s rovinou, na které jsou tělesa umístěna, a mají od této roviny stejnou vzdálenost, že obsah řezu T_1 je roven obsahu řezu T_2, mají obě tělesa stejný objem.
V následujícím appletu (obr. 2.4.7), kde jsou zobrazena dvě tělesa T_1, T_2, pohybujte bodem V. Počáteční pohled na tělesa je zobrazen v nárysu, v appletu lze měnit pohled na tělesa. Je možné pozorovat, že obsah řezů S_{T_1} a S_{T_2} rovinami rovnoběžnými s rovinou, na které jsou tělesa umístěna, je stále stejný. Počáteční pohled na tělesa je zachycen v nárysu. Dále je možné otáčet pohled na tělesa.
Obrázek 2.4.7: Applet – Ilustrace Cavalieriho principu; řezy těles T_1, T_2 rovinami rovnoběžnými s rovinou, na které jsou tělesa umístěna
Poznámka
Tento způsob určení objemu je pojmenován po italském matematikovi jménem Bonaventura Cavalieri (1598‐1647), který byl žákem Galilea Galileiho.
Cavalieriho princip lze názorně vymodelovat pomocí sloupečku mincí, karet nebo ruletních žetonů. Sloupec žetonů má týž objem při zachování výšky sloupečku, ať žetony tvoří svislý či šikmý sloupec (obr. 2.4.8, obr. 2.4.9). Na obr. 2.4.8 se nacházejí dva svislé sloupce žetonů, které představují model válce a kvádru. Na obr. 2.4.9 se nacházejí dva šikmé sloupce žetonů.


Poznámka
Ve středoškolské matematice Cavalieriho princip nedokazujeme, neboť důkaz vychází ze znalostí integrálního počtu.
Povrch
Obsah rovinného obrazce se ve školské matematice zavádí obvykle takto [9b]:
Obsah S obrazce je kladné číslo, přiřazené obrazci tak, že platí:
1. Shodné obrazce mají sobě rovné obsahy.
2. Jestliže je obrazec složen z několika nepronikajících se obrazců, je jeho obsah roven součtu obsahů dílčích obrazců (aditivita obsahu).
3. Obsah čtverce, jehož strana má délku 1 (mm, cm, m …), je roven 1 (mm², cm², m² …).
Povrch tělesa je zaveden v následující definici, která vychází z [5, s. 227] a z [9, s. 150]:
Povrchem S tělesa T se rozumí obsah plochy, která je hranicí tělesa T.
Povrch se značí písmenem S (počáteční písmeno latinského slova superficie znamenající právě povrch/obsah).
Poznámka
Je-li hranice tělesa složena z jednoduchých rovinných obrazců (např. mnohoúhelníků u mnohostěnů) nebo je-li „rozvinutelná“ do rovinné sítě (např. u rotačního válce či kužele viz obr. 2.4.10), pak povrch tělesa je roven součtu obsahů rovinných obrazců, z nichž se hranice (resp. síť hranice) skládá.
Obrázek 2.4.10: Síť kužele
Položme si otázku, v jakých případech nelze hranici tělesa rozvinout do rovinné sítě. Vzpomeňme si na část kůry z oloupaného pomeranče nebo na odtržený kus míče, u kterých se nám nepodaří jejich fragmenty „rozvinout“ čili „narovnat“ do roviny (obr. 2.4.11). Síť koule tedy neexistuje.

Obrázek 2.4.11: Pomerančová kůra nerozložitelná do rovinné sítě
V případě, že bychom chtěli určit povrch tělesa, jehož hranici neumíme rozvinout do rovinné sítě, lze povrch tělesa pokrýt tenkou vrstvou materiálu (například alobalu) a na základě jeho hustoty a hmotnosti určit objem tělesa. Zvážíme materiál, kterým jsme pokryli těleso. Hmotnost m použitého materiálu je
m = \rho \cdot V,
kde \rho je hustota materiálu a V je objem materiálu. Vyjádříme objem materiálu, který je
V= \frac{m}{\rho}.
Pak můžeme přibližně určit povrch tělesa
S \doteq \frac{V}{d},
kde d označuje tloušťku materiálu. Čím bude vrstva použitého materiálu tenčí, tím bude povrch určen přesněji. Pro přesnou geometrickou úvahu, pomocí níž lze definovat povrch i takovýchto těles, jejíchž hranice se neskládá jen z rovinných obrazců, je třeba znát limitní počet.
Povrch S je také fyzikální veličina, ke které je přiřazena číselná hodnota a jednotka. Číselná hodnota je závislá na volbě jednotky. Měřící jednotkou povrchu je metr čtvereční (značka m^2). Z m^2 jsou vyjádřeny násobky nebo díly pomocí dekadických předpon (mm^2, cm^2, dm^2, km^2). Pro specializované oblasti se používají vedlejší jednotky. Výměra pozemků se udává v arech (ar) nebo hektarech (ha). Za nestandardní jednotku povrchu se považuje například akr (anglo-americká měrná jednotka, 1 akr = 0,404 685 hektaru).
Následuje tabulka (tab. 2.4.3) převodních vztahů pro milimetr krychlový (mm²), centimetr krychlový (cm²), decimetr krychlový (dm²), metr krychlový (m²), kilometr krychlový (km²), ar (ar) a hektar (ha).
| 1 mm² | = | 0,01 cm² | = | 0,000 1 dm² | = | 0,000 001 m² | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 mm² | = | 1 cm² | = | 0,01 dm² | = | 0,000 1 m² | ||||||
| 10 000 mm² | = | 100 cm² | = | 1 dm² | = | 0,01 m² | ||||||
| 1 000 000 mm² | = | 10 000 cm² | = | 100 dm² | = | 1 m² | = | 0,01 ar | = | 0,000 1 ha | = | 0,000 001 km² |
| 100 m² | = | 1 ar | = | 0,01 ha | = | 0,000 1 km² | ||||||
| 10 000 m² | = | 100 ar | = | 1 ha | = | 0,01 km² | ||||||
| 1 000 000 m² | = | 10 000 ar | = | 100 ha | = | 1 km² |
Tabulka 2.4.3 – Převodní vztahy jednotek obsahu
