Objemy a povrchy těles

Objemy a povrchy nekonvexních mnohostěnů

V této kapitole se budeme zabývat nekonvexními mnohostěny, se kterými se ve středoškolských učebnicích zřídka setkáváme. Ze světa kolem nás si uvedeme několik architektonických staveb ve tvaru nekonvexních mnohostěnů (obr. 5.1.1–5.1.5).

Obrázek 5.1.1: Budova Civil Justice Centre (Manchester, Velká Británie) [37]

Obrázek 5.1.2: Wotrubův kostel (Vídeň, Rakousko) [38]

Obrázek 5.1.3: Komplex budov Habitat 67 (Montreal, Quebec) [39]

Obrázek 5.1.4: Mrakodrap MahaNakhon (Bangkok, Thajsko) [40]

Obrázek 5.1.5: Budova Čínské ústřední televize (Peking, Čína) [41]

Následně si uvedeme několik příkladů s řešením a krokovaných úloh na výpočet objemu a povrchu nekonvexních mnohostěnů.

Příklad 5.1.1

Vypočtěte objem V a povrch S_h nekonvexního kolmého pětibokého hranolu A_1A_2A_3A_4A_5A_6A_7A_8A_9A_{10} vyobrazeném na obr. 5.1.1. Obsah S nekonvexního pětiúhelníku A_1A_2A_3A_4A_5 je 8,44 cm^2. Délky stran nekonvexního pětiúhelníku A_6A_7A_8A_9A_{10} jsou a_1=5 cm, a_2=a_5=3 cm a a_3=a_4=2 cm. Tělesová výška v hranolu je 7 cm. Výsledky uveďte na jedno desetinné místo.

Obrázek 5.1.6: Applet – ilustrace k Příkladu 5.1.1

Řešení

Pro objem V libovolného hranolu platí V = S_pv. Výška v tohoto hranolu měří 7 cm.
Podstavy daného hranolu jsou navzájem shodné nekonvexní pětiúhelníky (obr. 5.1.6). Podstavy tělesa jsou shodné útvary, mají tedy i shodné obsahy. Pro obsah podstavy platí S_p = S_{A_1A_2A_3A_4A_5} = 8,44 cm^2.
Vypočítáme objem V tohoto hranolu: V = S_pv = 8,44 cm^2 \cdot 7 cm \doteq 59,1 cm^3.
Pro povrch S_h hranolu platí vztah S_h = 2S_p + S_{pl}.
Obsah pláště S_{pl} nekonvexního kolmého pětibokého hranolu je rovnen součtu obsahů všech bočních stěn. U tohoto hranolu jsou boční stěny tvořeny pěti obdélníky A_1A_2A_7A_6, A_2A_3A_8A_7, A_3A_4A_9A_8, A_4A_5A_{10}A_9 a A_5A_1A_6A_{10}, z nichž dvě dvojice stěn jsou shodné: A_2A_3A_8A_7 \cong A_5A_1A_6A_{10} a A_3A_4A_9A_8 \cong A_4A_5A_{10}A_9. Tedy S_{pl} = 2S_{A_2A_3A_8A_7} + 2S_{A_3A_4A_9A_8} + S_{A_1A_2A_7A_6}.
Vypočítáme obsah obdélníku A_2A_3A_8A_7: S_{A_2A_3A_7A_8} = a_2 \cdot v = 3 cm \cdot 7 cm = 21 cm^2.
Vypočítáme obsah obdélníku A_3A_4A_9A_8: S_{A_3A_4A_9A_8} = a_3 \cdot v = 2 cm \cdot 7 cm = 14 cm^2.
Vypočítáme obsah obdélníku A_1A_2A_7A_6: S_{A_1A_2A_7A_6} = a_1 \cdot v = 5 cm \cdot 7 cm = 35 cm^2.
Vypočítáme obsah pláště S_{pl} tohoto hranolu:
S_{pl} = 2S_{A_2A_3A_8A_7} + 2S_{A_3A_4A_9A_8} + S_{A_1A_2A_7A_6} = 2 \cdot 21 cm^2 + 2 \cdot 14 cm^2 + 35 cm ^2 = 105 cm^2.
Vypočítáme povrch S_h tohoto hranolu:
S_h = 2S_p + S_{pl} = 2 \cdot 8,44 cm^2 + 105 cm^2 \doteq 121,9 cm^2.
Objem nekonvexního kolmého pětibokého hranolu A_1A_2A_3A_4A_5A_6A_7A_8A_9A_{10} je 59,1 cm^3 a jeho povrch je 121,9 cm^2.

Příklad 5.1.2

Vypočtěte objem V_j a povrch S nekonvexního šestibokého jehlanu A_1A_2A_3A_4A_5A_6V, který vznikl z pravidelného čtyřbokého jehlanu A_1XA_5A_6V o podstavné hraně a = 6 cm a tělesové výšce v = 8 cm „odříznutím“ čtyřbokého jehlanu A_2XA_4A_3V se čtvercovou podstavou o straně \frac{a}{2} a stejné tělesové výšce, viz obr. 5.1.2. Bod A_3 je patou tělesové výšky v, |A_3V|= 8 cm, body S_{A_1A_6}, S_{A_5A_6} jsou středy příslušných hran. Výsledky zaokrouhlete na jedno desetinné místo.

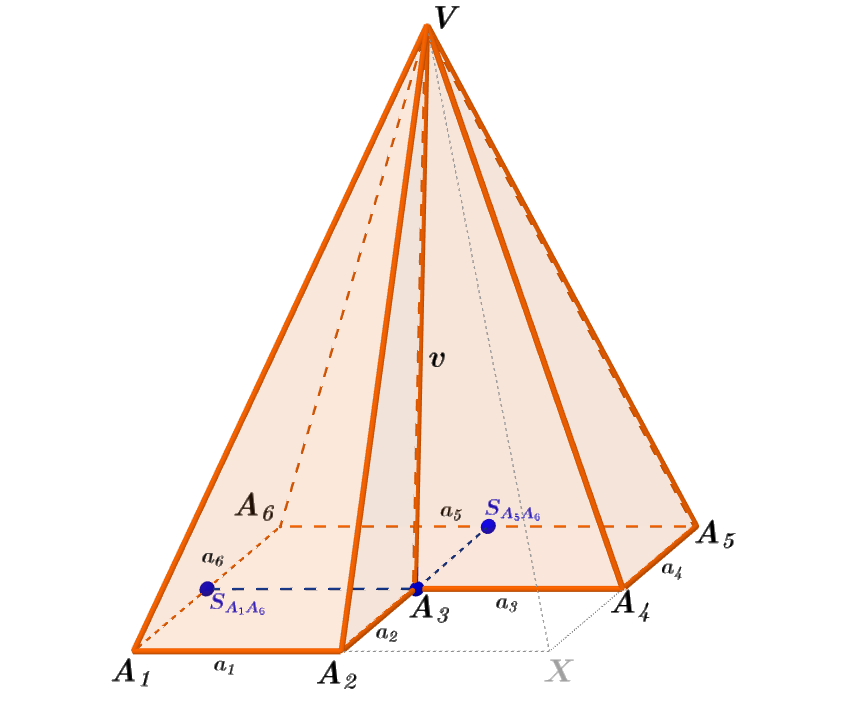
Obrázek 5.1.7: Ilustrace k Příkladu 5.1.2

Řešení

Pro objem V_j jehlanu platí V_j = \frac{1}{3}S_pv. Výšku v tohoto jehlanu známe; v = |A_3V| = 8 cm.
Délky podstavných hran jsou {a_1=a_2=a_3=a_4=3} cm a {a_5=a_5=6} cm (obr. 5.1.7).
Ukážeme si tři způsoby výpočtu objemu daného nekonvexního šestibokého jehlanu A_1A_2A_3A_4A_5A_6V:
1. - Obsah podstavy S_p tohoto jehlanuu je roven obsahu nekonvexního šestiúhelníku A_1A_2A_3A_4A_5A_6, který lze rozdělit na tři shodné nepřekrývající se čtverce A_1A_2A_3 S_{A_1A_6}, A_3A_4A_5 S_{A_5A_6} a A_3 S_{A_5A_6}A_6 S_{A_1A_6} o straně a = 3 cm.
  - Vypočítáme obsah jednoho ze čtverců: S_{A_1A_2A_3 S_{A_1A_6}}=a^2 = 3^2 cm^2 = 9 cm^2.
  - Vypočítáme obsah podstavy: S_p = 3 \cdot S_{A_1A_2A_3 S_{A_1A_6}} = 3 \cdot 9 cm^2 = 27 cm^2.
  - Vypočítáme objemu jehlanu: V_j = \frac{1}{3}S_pv = \frac{1}{3} \cdot 27 cm^2 \cdot 8 cm = 72 cm^3.
2. - Daný jehlan A_1A_2A_3A_4A_5A_6V lze rozdělit na tři shodné nepronikající se čtyřboké jehlany A_1A_2A_3 S_{A_1A_6}V, A_3A_4A_5 S_{A_5A_6}V a A_3 S_{A_5A_6}A_6 S_{A_1A_6}V, jejichž podstavy jsou shodné čtverce o straně a = 3 cm. Tyto čtyřboké jehlany mají shodnou tělesovou výšku v = |A_3V| = 8 cm.
  - Objem nekonvexního šestibokého jehlanu je roven součtu objemů tří shodných čtyřbokých jehlanů, které se nepronikají. Vypočítáme obsah podstavy a také objem jednoho z nich: S_{A_1A_2A_3 S_{A_1A_6}} = a^2 = 3^2 cm^2 = 9 cm^2,
    V_{A_1A_2A_3 S_{A_1A_6}V} = \frac{1}{3} S_{A_1A_2A_3 S_{A_1A_6}}v = \frac{1}{3} 9 cm^2 \cdot 8 cm = 24 cm^3.
  - Vypočítáme objem nekonvexního jehlanu: V_j = 3 V_{A_1A_2A_3 S_{A_1A_6}V} = 3 \cdot 24 cm^3 = 72 cm^3.
Pro povrch S jehlanu platí S = S_p + S_{pl}; S_p jsme již vypočítali: S_p = 3 \cdot S_{A_1A_2A_3 S_{A_1A_6}} = 27 cm^2.
Obsah pláště S_{pl} nekonvexního šestibokého jehlanu je rovnen součtu obsahů všech bočních stěn. U tohoto jehlanu jsou boční stěny tvořeny šesti trojúhelníky A_1A_2V, A_2A_3V, A_3A_4V, A_4A_5V, A_5A_6V a A_6A_1V, přičemž tři dvojice těchto trojúhelníků jsou shodné: \triangle A_1A_2V \cong \triangle A_4A_5V, \triangle A_2A_3V \cong \triangle A_3A_4V a \triangle A_5A_6V \cong \triangle A_6A_1V. Tedy S_{pl} = 2S_{A_1A_2V} + 2S_{A_2A_3V} + 2S_{A_5A_6V}.
Vypočítáme obsah pravoúhlého trojúhelníku A_1A_2V: S_{\triangle A_1A_2V} = \frac{a_1\ \cdot\ v_{a_1}}{2}; výška v_{a_1} = A_2V = S_{A_5A_6}V; úsečka S_{A_5A_6}V je také ramenem rovnoramenného \triangle A_2S_{A_5A_6}V, který rozdělíme podle jeho výšky v na dva pravoúhlé trojúhelníky. Z pravoúhlého \triangle A_3S_{A_5A_6}V vypočítáme Pýthagorovou větou délku jeho přepony S_{A_5A_6}V: |S_{A_5A_6}V| = \sqrt{3² + 8²} cm = \sqrt{73} cm \doteq 8,54 cm; |S_{A_5A_6}V| = v_{a_1} = 8,54 cm. Tedy S_{\triangle A_1A_2V} = \frac{a_1\ \cdot\ v_{a_1}}{2} = \frac{3\ \cdot\ 8,54}{2} cm = 12,81 cm^2.
Vypočítáme obsah pravoúhlého trojúhelníku A_2A_3V: S_{\triangle A_2A_3V} = \frac{a_2\ \cdot\ v_{a_2}}{2}; přičemž v_{a_2} = v = 8 cm.
Tedy S_{\triangle A_2A_3V} = \frac{a_2\ \cdot\ v}{2} = \frac{3\ \cdot\ 8}{2} cm = 12 cm^2.
Vypočítáme obsah rovnoramenného trojúhelníku A_5A_6V: S_{\triangle A_5A_6V} = \frac{1}{2} a_5\ \cdot\ v_{a_5}; přičemž v_{a_5} = S_{A_5A_6}V = v_{a_1} = 8,54 cm. Tedy S_{\triangle A_5A_6V} = \frac{a_5\ \cdot\ v_{a_5}}{2} = \frac{6\ \cdot\ 8,54}{2} cm = 25,62 cm^2.
Vypočítáme obsah pláště S_{pl} tohoto jehlanu:
S_{pl} = 2S_{A_1A_2V} + 2S_{A_2A_3V} + 2S_{A_5A_6V} = 2\ \cdot\ 12,81 cm^2\ +\ 2\ \cdot\ 12 cm^2\ +\ 2\ \cdot\ 25,62 cm^2 = 100,86 cm^2.
Vypočítáme povrch S tohoto hranolu:
S = S_p + S_{pl} = 27 cm^2 + 100,86 cm^2 \doteq 127,9 cm^2.
Objem daného nekonvexního kolmého pětibokého hranolu je 72 cm^3 a jeho povrch je 127,9 cm^2.

Příklad 5.1.3

Vypočtěte objem V a povrch S nekonvexního dvanáctistěnu A_1B_1C_1D_1E_1F_1G_1H_1A_2B_2C_2D_2E_2F_2G_2H_2 vyobrazeném na appletu (obr. 5.1.3). Bod S je středem pomyslné pomocné krychle A_1B_1C_1D_1E_1F_1G_1H_1 i vnitřní dutiny ve tvaru krychle A_2B_2C_2D_2E_2F_2G_2H_2. Dále platí |A_1A_2| = |A_2S| = \sqrt{3} m, poměr délek úseček |A_1A_2|:|A_2G_1| je roven 1:3.

Obrázek 5.1.8: Applet – ilustrace k Příkladu 5.1.3

Řešení

Objem V daného dvanáctistěnu vypočítáme tak, že od objemu V_1 krychle A_1B_1C_1D_1E_1F_1G_1H_1 o hraně a_1 odečteme objem V_2 krychle A_2B_2C_2D_2E_2F_2G_2H_2 o hraně a_2: V = V_{A_1B_1C_1D_1E_1F_1G_1H_1} - V_{A_2B_2C_2D_2E_2F_2G_2H_2}.
Pro objem V_1 platí V_1 = V_{A_1B_1C_1D_1E_1F_1G_1H_1} = {a_1}^3. Musíme tedy určit a_1.
Vypočítáme délku hrany a_1 krychle A_1B_1C_1D_1E_1F_1G_1H_1. Pro stěnovou úhlopříčku u_{s_1} krychle o hraně a_1 platí u_{s_1} = a_1 \sqrt{2}; pro tělesovou úhlopříčku u_{t_1} krychle o hraně a_1 platí u_{t_1} = a_1 \sqrt{3}. Vycházíme z pravoúhlého \triangle A_1C_1G_1: A_1C_1 = u_{s_1} = a_1 \sqrt{2}, C_1G_1 = a_1, G_1A_1 = u_{t_1} = a_1 \sqrt{3}. Víme, že |A_1A_2| = \sqrt{3} m; |A_1A_2|:|A_2G_1| = 1:3; u_t = |A_1G_1| = 4 \cdot |A_1A_2| = 4 \sqrt{3} m. Tedy a_1 = 4 m.
Vypočítáme objem krychle A_1B_1C_1D_1E_1F_1G_1H_1: V_1 = {a_1}^3 = 64 m^3.
Pro objem V_2 platí V_2 = V_{A_2B_2C_2D_2E_2F_2G_2H_2} = {a_2}^3.
Vypočítáme délku hrany a_2 krychle A_2B_2C_2D_2E_2F_2G_2H_2. Pro stěnovou úhlopříčku u_{s_2} krychle o hraně a_2 platí u_{s_2} = a_2\sqrt{2}; pro tělesovou úhlopříčku u_{t_2} krychle o hraně a_2 platí u_{t_2} = a_2\sqrt{3}. Vycházíme z pravoúhlého \triangle A_2C_2G_2: A_2C_2 = u_{s_2} = a_2\sqrt{2}, C_2G_2 = a_2, G_2A_2 = u_{t_2} = a_2\sqrt{3}. Víme, že |A_2S| = \sqrt{3} m; |A_2S|:|SG_2| = 1:1; u_{t_2} = |A_2G_2| = 2 \cdot |A_2S| = 2 \sqrt{3} m. Tedy a_2 = 2 m.
Vypočítáme objem krychle A_2B_2C_2D_2E_2F_2G_2H_2: V_2 = {a_2}^3 = 8 m^3.
Vypočítáme objem dvanáctistěnu: V = V_1 - V_2 = 64 m^3 - 8 m^3 = 56 m^3.
Povrch S mnohostěnu vypočítáme tak, že spočítáme obsah jeho sítě čili sečteme obsahy všech jeho stěn. Jeho stěny jsou tvořeny šesti shodnými čtverci o straně a_1 a šesti shodnými čtverci o straně a_2: S = (6 \cdot {a_1}^2) + (6 \cdot {a_2}^2) = 96 m^2 + 24 m^2 = 120 m^2.
Objem dvanáctistěnu je 56 m^3 a jeho povrch je 120 m^2.

Příklad 5.1.4

Vyjádřete objem V a povrch S devítistěnu ABCDEFGHS vyobrazeném na appletu (obr. 5.1.4). Bod S je středem pomyslné pomocné krychle ABCDEFGH o hraně a.

Obrázek 5.1.9: Applet – ilustrace k Příkladu 5.1.4

Řešení

Objem V daného devítistěnu vyjádříme tak, že od objemu V_1 krychle ABCDEFGH o hraně a odečteme objem V_2 pravidelného čtyřbokého jehlanu ABFES s výškou \frac{1}{2}a: V = V_{ABCDEFGH} - V_{ABFES}.
Pro objem V_1 platí V_1 = a^3.
Pro objem V_2 platí V_2 = \frac{1}{3} S_pv = \frac{1}{3} a^2 \frac{1}{2} \cdot a = \frac{1}{6} a^3.
Vyjádříme objem dvanáctistěnu: V = V_1 - V_2 = a^3 - \frac{1}{6} a^3 = \frac{5}{6} a^3.
Povrch S mnohostěnu určíme tak, že vyjádříme obsah jeho sítě čili sečteme obsahy všech jeho stěn. Jeho stěny jsou tvořeny pěti shodnými čtverci o straně a a čtyřmi shodnými rovnoramennými trojúhelníky o základně a a výšce v_a. Tedy S = 5a^2 + 4 \frac{a\ \cdot\ v_a}{2}.
Pro určení v_a potřebujeme znát délku b ramena rovnoramenného trojúhelníku, kterou vyjádříme pomocí délky tělesové úhlopříčky u_t krychle ABCDEFGH o hraně délky a takto: b = \frac{1}{2} u_t = \frac{1}{2} a\sqrt{3}. Výšku v_a (která je zároveň těžnicí) rovnoramenného trojúhelníku o základně délky a a ramenech délky b vyjádříme pomocí Pýthagorovy věty z pravoúhlého \triangle S_{AB}BS; v_a = \sqrt{b^2 - (\frac{a}{2})^2} = \sqrt{({\frac{1}{2} a\sqrt{3}})^2 - (\frac{a}{2})^2} = \sqrt{\frac{a^2}{2}} = \frac{\sqrt{2}}{2}a.
Vyjádříme povrch tohoto devítistěnu: S = 5a^2 + 4 \frac{a\ \cdot\ v_a}{2} = 5a^2 + 4 \frac{a\ \cdot\ \frac{\sqrt{2}}{2}a}{2} = 5a^2 + a^2\sqrt{2} = a^2(5 + \sqrt{2}).
Objem V nekonvexního devítistěnu ABCDEFGHS je V = \frac{5}{6} a^3 a jeho povrch je S = a^2(5 + \sqrt{2}).

Úloha 5.1.1

Na appletu (obr. 5.1.6) je dán dům se střechou ve tvaru čtyřbokého jehlanu včetně rozměrů domu. Vypočítejte povrch obvodových zdí (otvory pro okna zanedbejte) a objem střechy (půdy) tohoto domu.

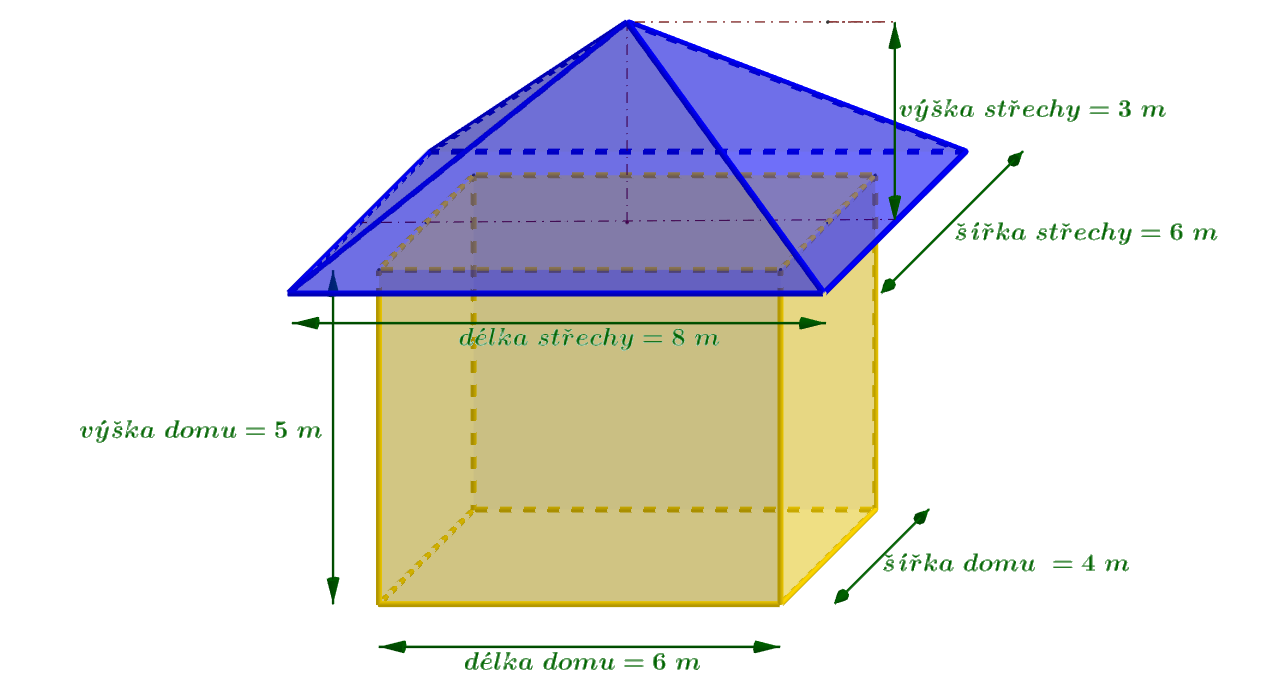
Obrázek 5.1.10: Ilustrace k Úloze 5.1.1

Pro určení povrchu obvodových zdí tohoto domu, musíme vypočítat obsah stěn, které tvoří obvodové zdi.
Obvodové zdi domu jsou tvořeny dvěma dvojicemi navzájem shodných obdélníků.
První dvojice obdélníků má rozměry délky domu a=6 m a výšky domu c=5 m. Obsah S_1 tohoto obdélníku je S_1 = a \cdot c = 6 m\ \cdot\ 5 m = 30 m^2.
Druhá dvojice obdélníků má rozměry šířky domu b=4 m a výšky domu c=5 m. Obsah S_2 tohoto obdélníku je S_2 = b \cdot c = 4 m\ \cdot\ 5 m = 20 m^2.
Vypočítáme obsah S_O obvodových stěn: S_O = 2S_1 + 2S_2 = 2\cdot30 m^2 + 2\cdot20 m^2 = 100 m^2.
Pro určení objemu půdy tohoto domu, musíme vypočítat objem V čtyřbokého jehlanu, jehož podstava je obdélník o rozměrech délky střechy d=8 m a šířky střechy e=6 m a jehož výška v je rovna výšce střechy f=3 m.
Pro objem V jehlanu platí: V = \frac{1}{3}S_pv.
Obsah podstavy S_p tohoto čtyřbokého jehlanu je S_p = d \cdot e = 8 m\ \cdot\ 6 m = 48 m^2.
Pro objem jehlanu platí V = \frac{1}{3}S_pv = \frac{1}{3}S_pf = \frac{1}{3} \cdot 48 m^2 \cdot 3 m = 48 m^3.
Povrch obvodových zdí daného domu je 100 m^2 a objem jeho půdy je 48 m^3.

Úloha 5.1.2

Vypočítejte objem V tělesa vyobrazeném na obr. 5.1.6, které představuje model starověkého chrámu zvaného zikurrat. Je složeno z deseti stupňů – pravidelných čtyřbokých hranolů. Délka podstavné hrany prvního stupně je 40 m, každý další stupeň (hranol) má podstavnou hranu o 4 metry kratší. Výška v každého stupně (hranolu) je 2 m.

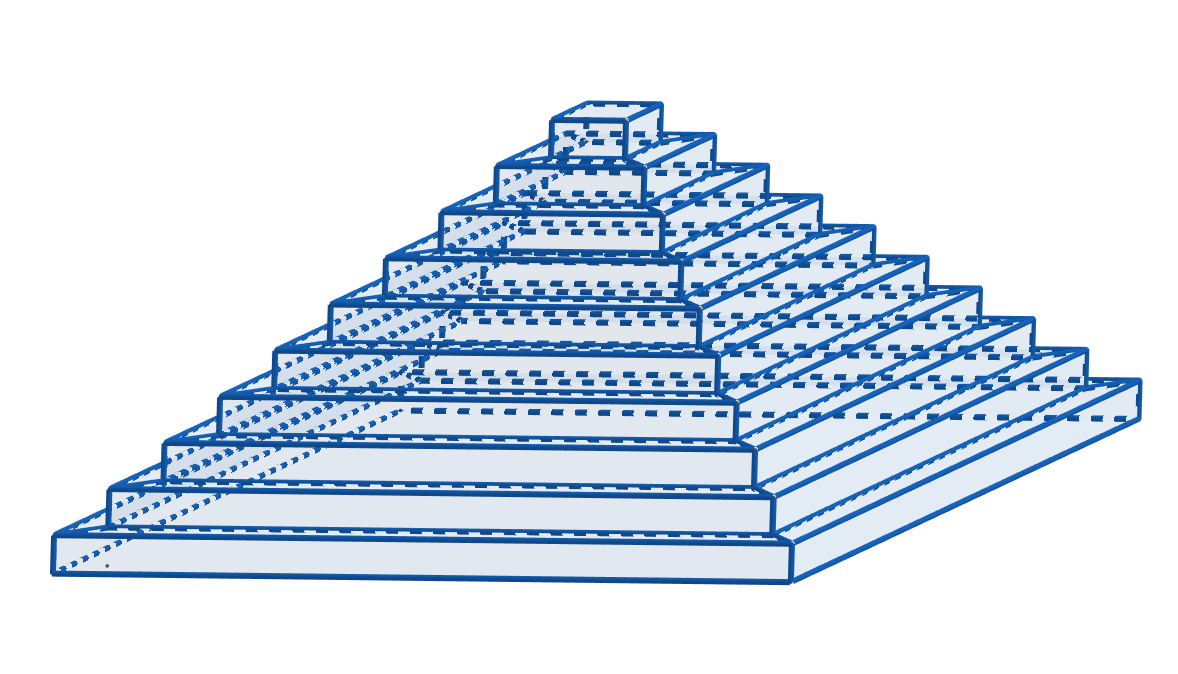
Obrázek 5.1.11: Ilustrace k Úloze 5.1.2

Objemu tohoto nekonvexního tělesa je roven součtu objemů V_i (i = 1, 2, \ldots, 9, 10) jednotlivých pravidelných čtyřbokých hranolů: V = V_1 + V_2 + V_3 + V_4 + V_5 + V_6 + V_7 + V_8 + V_9 + V_{10}.
Pro objem V_i (i = 1, 2, \ldots, 9, 10) každého pravidelného čtyřbokého hranolu platí: V_i = S_{p_i}v. Výška každého hranolu je rovna v = 2 m.
Určíme délky podstavných hran a_i (i = 1, 2, \ldots, 9, 10) jednotlivých hranolů; a_1 = 40 m: a_2 = 36 m; a_3 = 32 m; a_4 = 28 m; a_5 = 24 m; a_6 = 20 m; a_7 = 16 m; a_8 = 12 m; a_9 = 8 m; a_{10} = 4 m.
Vypočítáme obsahy podstav S_{p_i} (i = 1, 2, \ldots, 9, 10) jednotlivých hranolů; S_{p_i} = {a_i}^2: S_{p_1} = 1~600 m^2; S_{p_2} = 1~296 m^2; S_{p_3} = 1~024 m^2; S_{p_4} = 784 m^2; S_{p_5} = 576 m^2; S_{p_6} = 400 m^2; S_{p_7} = 256 m^2; S_{p_8} = 144 m^2; S_{p_9} = 64 m^2; S_{p_{10}} = 16 m^2.
Vypočítáme objemy V_i (i = 1, 2, \ldots, 9, 10) jednotlivých hranolů; V_i = S_{p_i}v: V_1 = 1~600 m^2 \cdot 2 m = 3~200 m^3; V_2 = 1~296 m^2 \cdot 2 m = 2~592 m^3; V_3 = 1~024 m^2 \cdot 2 m = 2~048 m^3; V_4 = 784 m^2 \cdot 2 m = 1~568 m^3; V_5 = 576 m^2 \cdot 2 m = 1~152 m^3; V_6 = 400 m^2 \cdot 2 m = 800 m^3; V_7 = 256 m^2 \cdot 2 m = 512 m^3; V_8 = 144 m^2 \cdot 2 m = 288 m^3; V_9 = 64 m^2 \cdot 2 m = 128 m^3; V_{10} = 16 m^2 \cdot 2 m = 32 m^3.
Vypočítáme objem V složeného nekonvexního tělesa:
V = V_1 + V_2 + V_3 + V_4 + V_5 + V_6 + V_7 + V_8 + V_9 + V_{10} = 3~200 m^3 +~2~592 m^3 +~2~048 m^3 +~1~568 m^3 +~1~152 m^3 +~800 m^3 +~512 m^3 + 288 m^3 +~128 m^3 +~32 m^3 = 12~320 m^3.
Objem modelu starověkého chrámu zvaného zikurrat je 12~320 m^3.

Úloha 5.1.3

Vypočítejte objem a povrch nekonvexního osmistěnu RSTUVW zobrazeném na obr. 5.1.7; toto těleso vzniklo „rozdílem“ dvou pravidelných čtyřbokých jehlanů se shodnými podstavami a různými výškami. Bod X je čtverceRSTU, |WX| = 8 km, |VX| = 4 km, a = |RS| = 6 km. Výsledky zaokrouhlete na jedno desetinné místo.

Obrázek 5.1.12: Applet – ilustrace k Úloze 5.1.3

Objem V nekonvexního osmistěnu RSTUVW vypočítáme tak, že od objemu V_1 pravidelného čtyřbokého jehlanu RSTUW o podstavné hraně a = 6 km a výšce v_1 = |WX| = 8 km odečteme objem V_2 pravidelného čtyřbokého jehlanu RSTUV o podstavné hraně a = 6 km a výšce v_2 = |WX| = 4 km: V = V_1 - V_2.
Pro objem V_1 platí V_1 = \frac{1}{3} S_pv_1 = a^2 \cdot v_1 = 36 km^2 \cdot 8 km= 288,00 km^3.
Pro objem V_2 platí V_2 = \frac{1}{3} S_pv_2 = a^2 \cdot v_2 = 36 km^2 \cdot 4 km= 144,00 km^3.
Vypočítáme objem nekonvexního osmistěnu: V = V_1 - V_2 = 288 km^3 - 144 km^3 = 144,0 km^3.
Povrch S mnohostěnu určíme tak, že vypočítáme obsah jeho sítě čili sečteme obsahy všech jeho stěn. Jeho stěny jsou tvořeny dvěma čtveřicemi rovnoramenných trojúhelníků, v každé čtveřici jsou trojúhelníky shodné. První čtveřice shodných rovnoramenných trojúhelníků má základnu a, délku ramen b a délku výšky v_3. Druhá čtveřice shodných rovnoramenných trojúhelníků má základnu a, délku ramen c a délku výšky v_4. Tedy S = 4 \cdot \frac{a\ \cdot\ v_3}{2} + 4 \cdot \frac{a\ \cdot\ v_4}{2}.
Body S_{RS}, S_{ST}, S_{TU}, S_{RU} jsou středy příslušných hran.
Pro určení výšky v_3 potřebujeme znát |WS_{RS}| = |WS_{TU}| = v_3, která je zároveň délkou ramene rovnoramenného trojúhelníku \triangle S_{RS}S_{TU}W. Tento rovnoramenný \triangle S_{RS}S_{TU}W o základně délky a = 6 km rozdělíme výškou v_1 na dva pravoúhlé trojúhelníky a vyjádříme v_3 pomocí Pýthagorovy věty: v_3 = \sqrt{{v_1}^2 + (\frac{a}{2})^2} = \sqrt{8^2 + (\frac{6}{2})^2} km = \sqrt{8^2 + 3^2} km = \sqrt{73} km \doteq 8,54 km.
Pro určení výšky v_4 potřebujeme znát |VS_{ST}| = |VS_{RU}| = v_4, která je zároveň délkou ramene rovnoramenného trojúhelníku \triangle S_{ST}S_{RU}V. Tento rovnoramenný \triangle S_{ST}S_{RU}V o základně délky a = 6 km rozdělíme výškou v_2 na dva pravoúhlé trojúhelníky a vyjádříme v_4 pomocí Pýthagorovy věty: v_4 = \sqrt{{v_2}^2 + (\frac{a}{2})^2} = \sqrt{4^2 + (\frac{6}{2})^2} km = \sqrt{4^2 + 3^2} km = \sqrt{25} km = 5 km.
Vypočítáme povrch tohoto osmistěnu:
S = 4 \cdot \frac{a\ \cdot\ v_3}{2} + 4 \cdot \frac{a\ \cdot\ v_4}{2} = 4 \cdot \frac{6\ \cdot\ 8,54}{2} km^2 + 4 \cdot \frac{6\ \cdot\ 5}{2} km^2 \doteq 4 \cdot 25,62 km^2 + 4 \cdot 15 km^2 \doteq 162,5 km^2.
Objem nekonvexního osmistěnu RSTUVW je 144,0 km^3 a jeho povrch je 162,5 km^2.

Objemy a povrchy těles

Objemy a povrchy nekonvexních mnohostěnů

Příklad 5.1.1

Řešení

Příklad 5.1.2

Řešení

Příklad 5.1.3

Řešení

Příklad 5.1.4

Řešení

Úloha 5.1.1

Úloha 5.1.2

Úloha 5.1.3

Titulní strana

Úvod

Motivace

Základní pojmy

Hranoly

Jehlany

Objemy a povrchy nekonvexních mnohostěnů

Souhrnný test

Rejstřík

Literatura a webové odkazy