Platónská tělesa
V této samostatné kapitole se budeme zabývat Platónovými či platónskými tělesy, protože jejich „dokonalé“ struktuře byla vždy věnována velká pozornost a tato tělesa našla uplatnění jak v architektuře nebo designu, tak třeba i v nanotechnologiích [1, s. 61–81].
Platónovo či platónské těleso je konvexní pravidelný mnohostěn, jehož všechny stěny jsou shodné pravidelné mnohoúhelníky a zároveň z každého vrcholu vychází stejný počet hran.
Pokud uvažujeme v rovině všechny pravidelné n-úhelníky, tak jich existuje nekonečně mnoho (n \in \mathbb{N}, n\ge3), zatímco pravidelných konvexních n-stěnů v prostoru existuje právě pět (obr. 2.3.1–2.3.5).
Pravidelný čtyřstěn
Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr. 2.3.1.
Obrázek 2.3.1: Applet – pravidelný čtyřstěn
Pravidelný šestistěn
Pravidelným šestistěnem je krychle. Jeho stěny jsou tvořeny šesti shodnými čtverci. Toto těleso má osm vrcholů a dvanáct hran, viz obr. 2.3.2.
Obrázek 2.3.2: Applet – pravidelný šestistěn
Pravidelný osmistěn
Stěny pravidelného osmistěnu jsou tvořeny osmi shodnými rovnostrannými trojúhelníky. Toto těleso si můžeme představit jako sjednocení dvou shodných těles, a to pravidelných čtyřbokých jehlanů se společnou podstavou. Toto těleso má šest vrcholů a dvanáct hran, viz obr. 2.3.3.
Obrázek 2.3.3: Applet – pravidelný osmistěn
Pravidelný dvanáctistěn
Stěny pravidelného dvanáctistěnu jsou tvořeny dvanácti shodnými pravidelnými pětiúhelníky. Toto těleso má dvacet vrcholů a třicet hran, viz obr. 2.3.4.
Obrázek 2.3.4: Applet – pravidelný dvanáctistěn
Pravidelný dvacetistěn
Stěny pravidelného dvacetistěnu jsou tvořeny dvaceti shodnými rovnostrannými trojúhelníky. Toto těleso má dvanáct vrcholů a třicet hran, viz obr. 2.3.5.
Obrázek 2.3.5: Applet – pravidelný dvacetistěn
Následující věta uvádí počet konvexních pravidelných mnohostěnů.
Existuje právě pět konvexních pravidelných mnohostěnů.
Předvedeme si důkaz, proč existuje právě pět konvexních pravidelných mnohostěnů. Plášť pravidelného mnohostěnu je tvořen shodnými pravidelnými mnohoúhelníky a žádné dva pravidelné mnohoúhelníky neleží ve stejné rovině. Součet velikostí vnitřních úhlů ve stěnách u jednoho vrcholu, ve kterém se sbíhají hrany, musí být menší než 360° (v opačném případě by stěny incidující s daným vrcholem ležely v jedné rovině) a zárověň každý vrchol mnohostěnu inciduje alespoň se třemi stěnami, aby mohlo vzniknout prostorové těleso.
- Stěnami mnohostěnu jsou rovnostranné trojúhelníky
- Stěnami mnohostěnu jsou pravidelné čtyřúhelníky – čtverce
- Stěnami mnohostěnu jsou pravidelné pětiúhelníky
- Stěnami mnohostěnu jsou pravidelné šestiúhelníky
Velikost vnitřních úhlů rovnostranného trojúhelníku je 60°. Na základě této skutečnosti se mohou v jednom vrcholu pravidelného mnohostěnu stýkat stěny tři (čtyřstěn), čtyři (osmistěn) nebo pět (dvacetistěn), kde součty velikostí úhlů u vrcholu budou popořadě 3 \cdot 60° = 180°, 4 \cdot 60° = 240° nebo 5 \cdot 60° = 300°, viz obr. 2.3.6. V případě počtu stěn vyššího než pět bychom již přesáhli omezující podmínku (6 \cdot 60° = 360°).
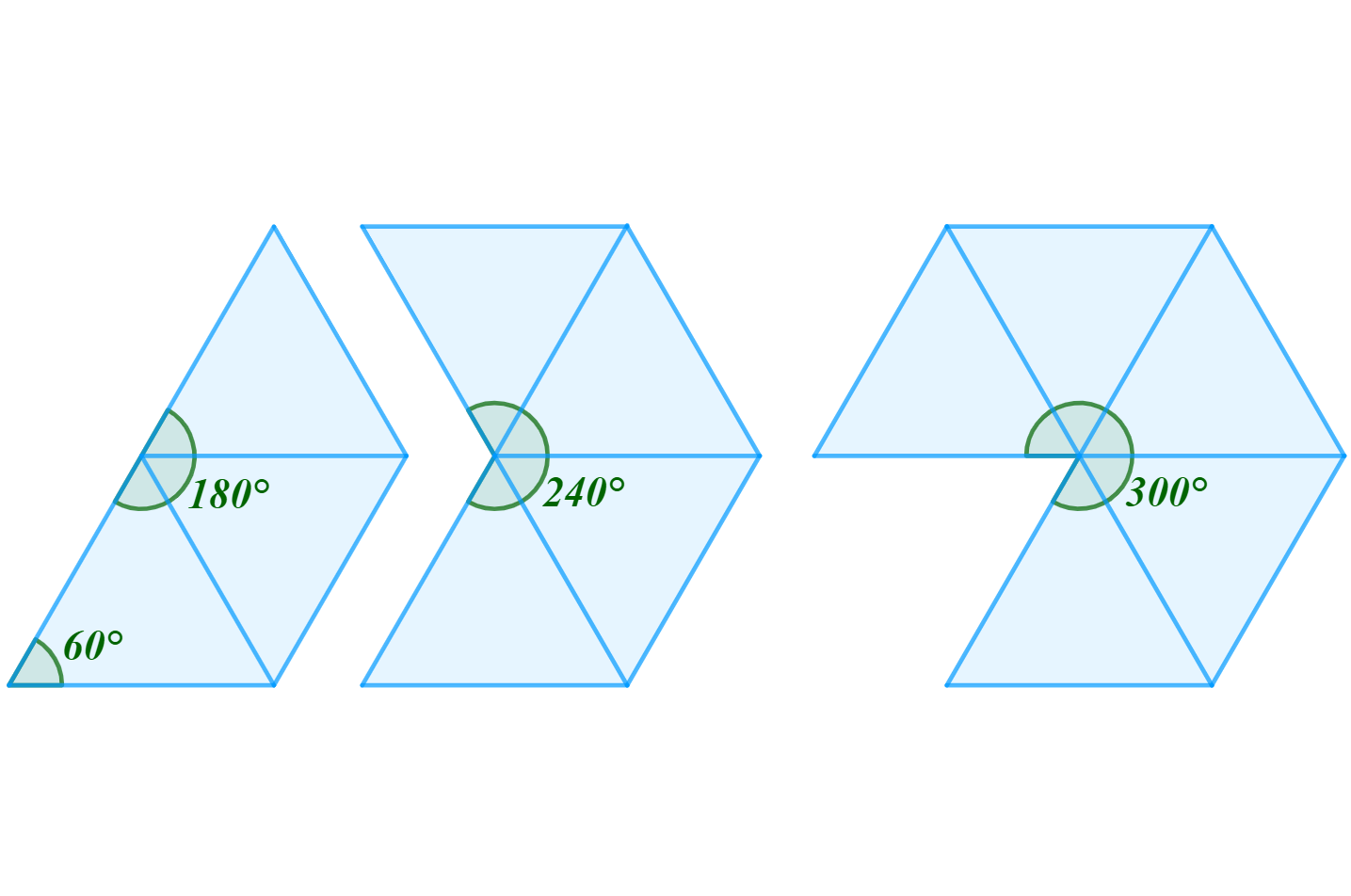
Obrázek 2.3.6: Součet velikostí úhlů u jednoho vrcholu pravidelného čtyřstěnu, osmistěnu a dvacetistěnu
Velikost vnitřních úhlů pravidelného čtyřúhelníku je 90°. Na základě této skutečnosti se mohou v jednom vrcholu pravidelného mnohostěnu stýkat pouze tři stěny (krychle), kde součet velikostí úhlů u vrcholu bude 3 \cdot 90° = 270°, viz obr. 2.3.7. V případě počtu stěn vyššího než tři bychom již přesáhli omezující podmínku (4 \cdot 90° = 360°).
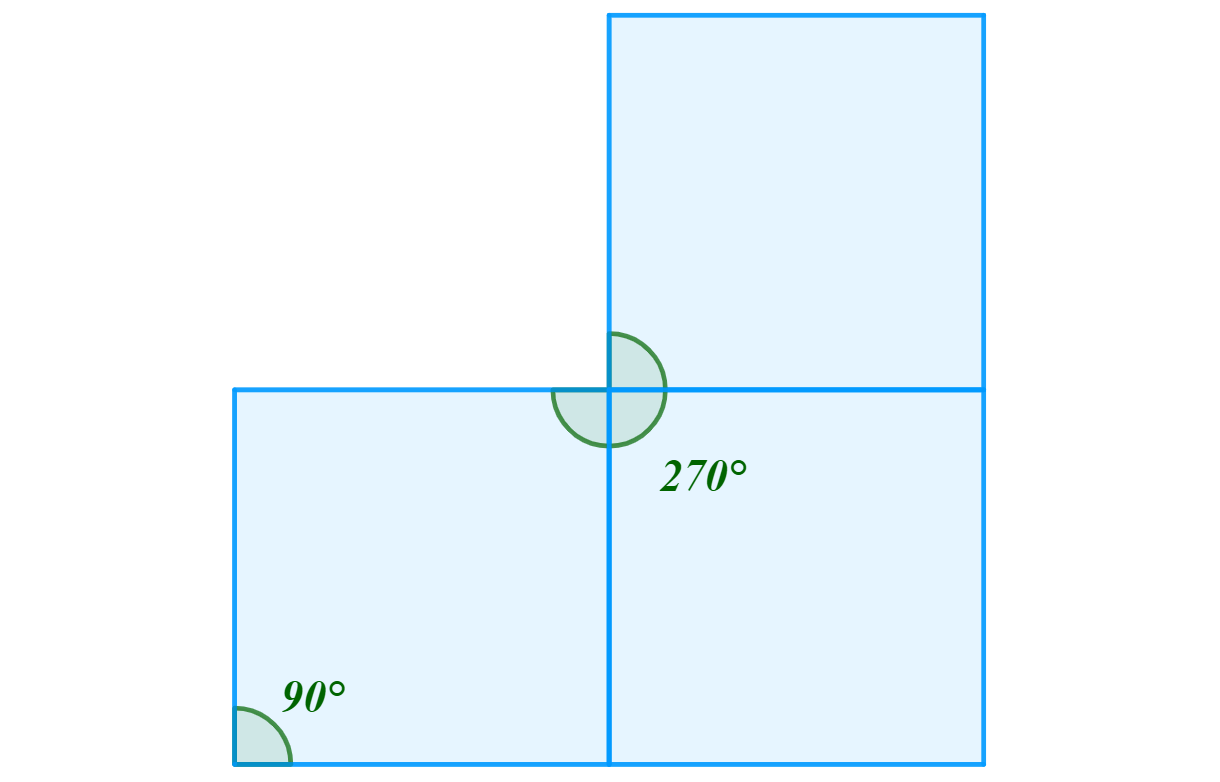
Obrázek 2.3.7: Součet velikostí úhlů u jednoho vrcholu krychle
Velikost vnitřních úhlů pravidelného pětiúhelníku je 108°. Na základě této skutečnosti se mohou v jednom vrcholu pravidelného mnohostěnu stýkat pouze tři stěny (dvanáctistěn), kde součet velikostí úhlů u vrcholu bude 3 \cdot 108° = 324°, viz obr. 2.3.8. V případě počtu stěn vyššího než tři bychom již přesáhli omezující podmínku (4 \cdot 108° = 432°).
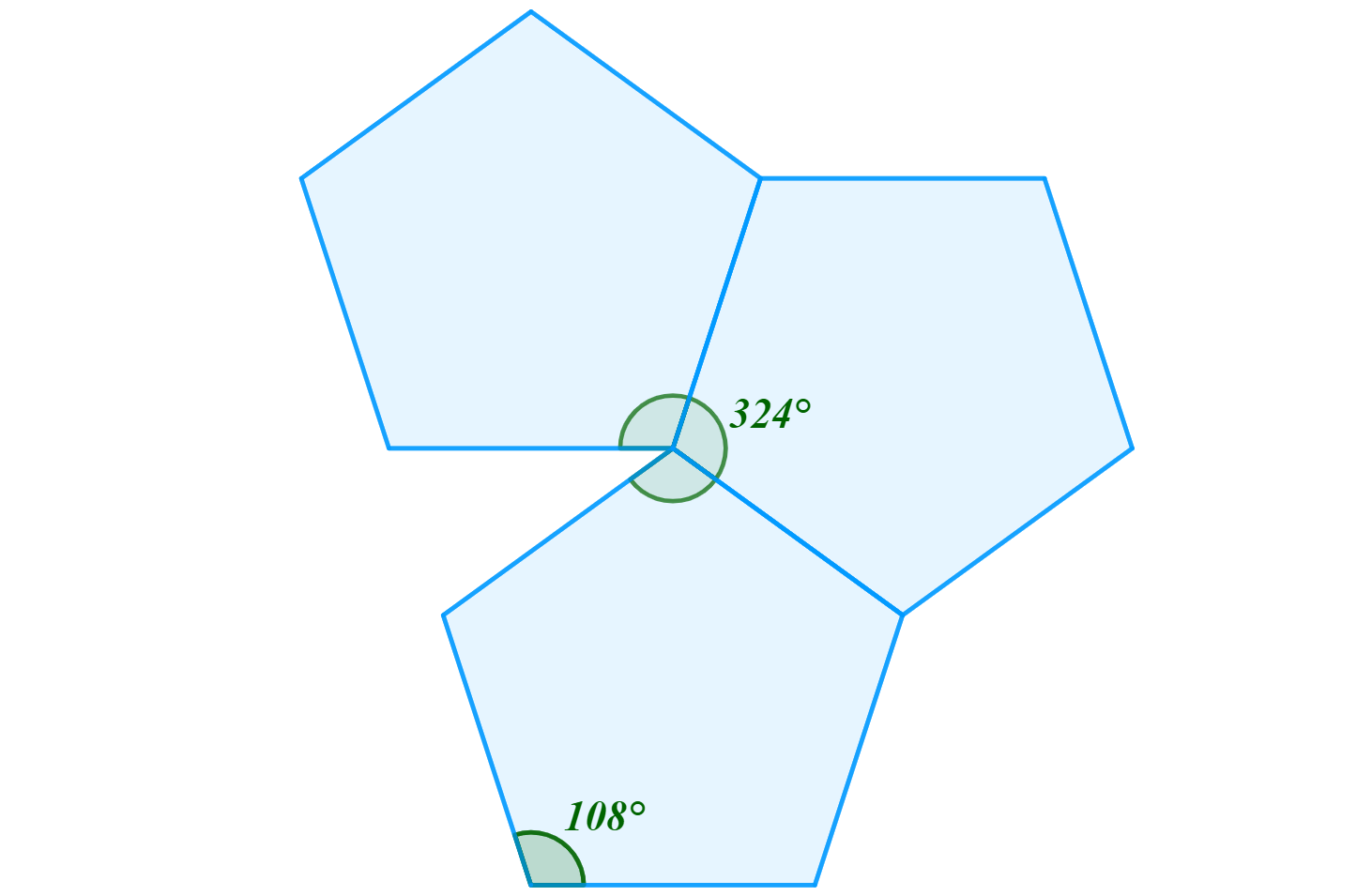
Obrázek 2.3.8: Součet velikostí úhlů u jednoho vrcholu pravidelného dvanáctistěnu
Velikost vnitřních úhlů pravidelného šestiúhelníku je 120°. Pokud se budou stýkat tři stěny v jednom vrcholu, tak součet velikostí úhlů u vrcholu bude 3 \cdot 120° = 360°. Tím jsme přesáhli omezující podmínku a stěny incidující s daným vrcholem leží v jedné rovině, proto neexistuje pravidelný konvexní mnohostěn, který by měl za stěny šestiúhelníky, viz obr. 2.3.9. Obdobně toto tvrzení platí pro pravidelné n-úhelníky s vyšším počtem vrcholů než šest. Tímto jsme ukázali, že pravidelných konvexních mnohostěnů je právě pět.
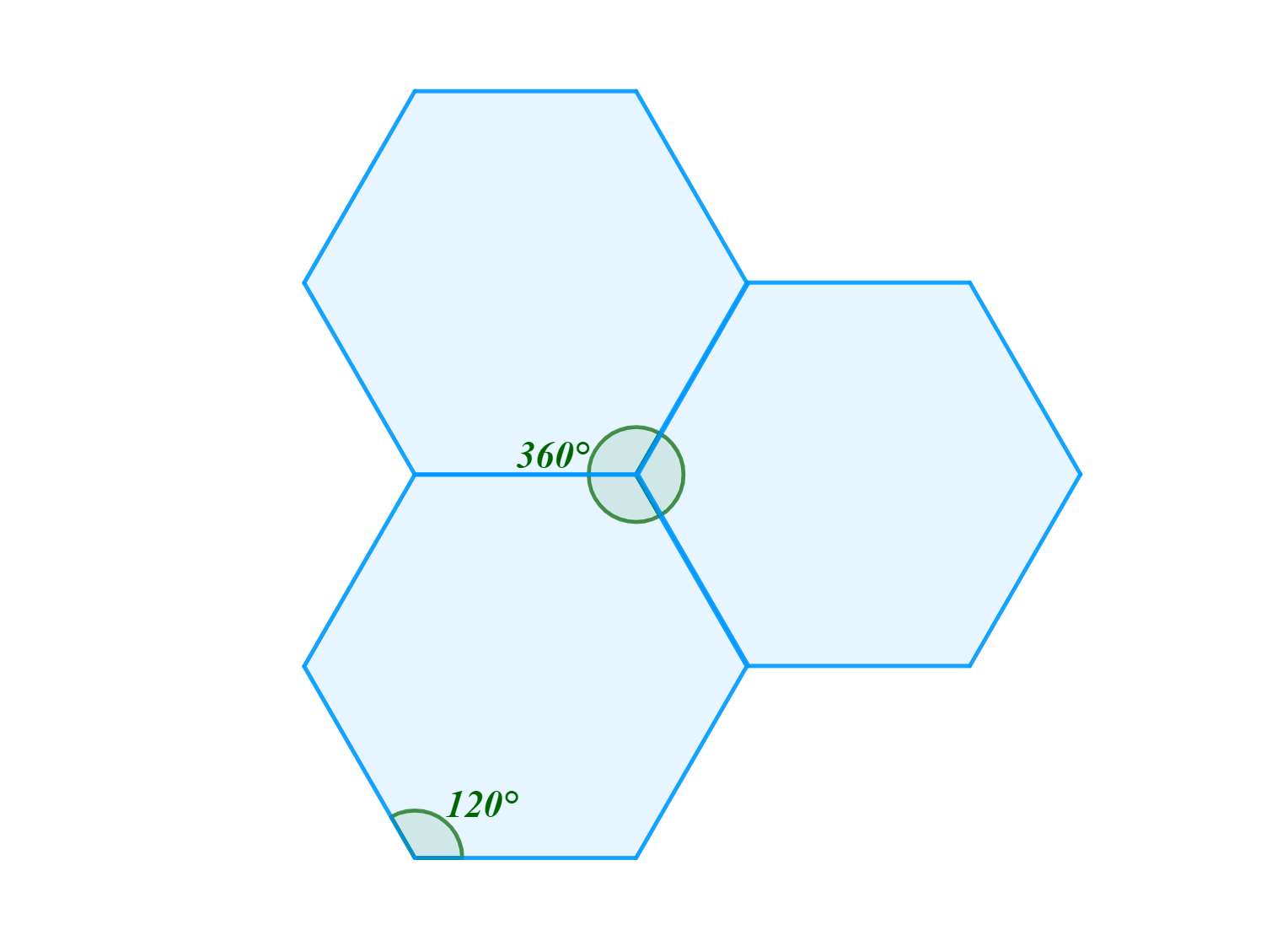
Obrázek 2.3.9: Šestiúhelníky incidující s daným vrcholem ležící v jedné rovině
Obdobně jako pravidelným mnohoúhelníkům vepisujeme a opisujeme kružnici, tak každému pravidelnému konvexnímu mnohostěnu (platónskému tělesu) je možné sestrojit vepsanou a opsanou kulovou plochu.
- Vepsaná kulová plocha se dotýká všech stěn platónského tělesa v jejich středech.
- Opsaná kulová plocha obsahuje všechny vrcholy platónského tělesa. Středy těchto dvou kulových ploch splývají v jednom bodě.
Dualita platónských těles
Následující definice je převzata z [4, str. 41].
Ke každému pravidelnému mnohostěnu existuje mnohostěn jemu duální, jehož vrcholy leží ve středech stěn mnohostěnu původního.
Tedy středy jednotlivých stěn platónského tělesa tvoří vrcholy dalšího platónského tělesa. Hrany nového mnohostěnu tvoří úsečky spojující vrcholy v sousedních stěnách. Takto získaný mnohostěn se nazývá duální mnohostěn k mnohostěnu výchozímu. Tuto vlastnost pojmenováváme jako dualita platónských těles. Pravidelný čtyřstěn je duální sám se sebou (obr. 2.3.10). Pravidelný šestistěn je duální s pravidelným osmistěnem a naopak (obr. 2.3.11, obr. 2.3.12). Pravidelný dvanáctistěn je duální s pravidelným dvacetistěnem a naopak (obr. 2.3.13, obr. 2.3.14).
Obrázek 2.3.10: Applet – dualní mnohostěn k čtyřstěnu – čtyřstěn
Obrázek 2.3.11: Applet – dualní mnohostěn ke krychli – osmistěn
Obrázek 2.3.12: Applet – dualní mnohostěn k osmistěnu – krychle
Obrázek 2.3.13: Applet – dualní mnohostěn k dvanáctistěnu – dvacetistěn
Obrázek 2.3.14: Applet – dualní mnohostěn k dvacetistěnu – dvanáctistěn
Platónská tělesa nacházejí uplatnění v různých oblastech lidské činnnosti, například z herního světa jsou známé hrací kostky vyobrazené na obr. 2.3.15. Na jejich stěnách se postupně nacházejí čísla od 1 do 6. V některých stolních hrách se hraje i s jinými tvary kostek (obr. 2.3.16), ale vždy kostky budou mít tvar pravidelného mnohostěnu, protože pravděpodobnost dopadu na jednotlivé stěny by měla být stejná.

Obrázek 2.3.15: Hrací kostka ve tvaru krychle [28]

Obrázek 2.3.16: Hrací kostky ze hry Dungeons & Dragons ve tvaru pravidelných mnohostěnů [36]
