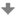Konstrukce elipsy
Osová afinita mezi elipsou a kružnicí
Mezi elipsou a kružnicí se středem v bodě S a poloměrem SA (resp. SC) je vztah osové afinity. Existují dva základní typy pravoúhlé osové afinity mezi elipsou a kružnicí:
- Osa afinity splývá s hlavní osou elipsy o1. Střed S´
kružnice splývá se středem elipsy S. Vrcholy A, B jsou samodružné (leží na ose afinity).
Kružnice e´ má střed v bodě S a poloměr SA. Chybí ještě
určit pár odpovídajících si bodů, např. C, C´. Protože hledáme pravoúhlou afinitu, bod C´
leží na kolmici k ose afinity procházející bodem C a na kružnici e´.
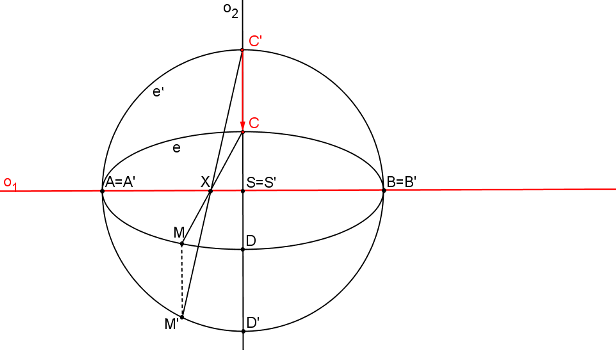
- Osa afinity splývá s vedlejší osou elipsy o2. Střed S´
kružnice splývá se středem elipsy S. Vrcholy C, D jsou samodružné (leží na ose afinity).
Kružnice e´ má střed v bodě S a poloměr SC. Pár odpovídajících si bodů,
např. dvojice A, A´, kde A´ leží na kolmici k ose afinity procházející bodem
A a na kružnici e´.
Trojúhelníková konstrukce
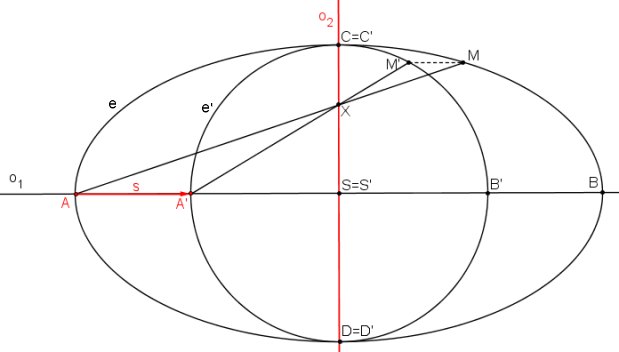
Elipsa je dána hlavními vrcholy A, B a vedlejšími vrcholy C, D. S je střed elipsy. Sestrojíme kružnici k1(S,a) (pozn. a je velikost hlavní poloosy) a kružnici k2(S,b) (pozn. b je velikost vedlejší poloosy). Na kružnici k1 libovolně zvolíme bod X1. Průsečík polopřímky SX1 a kružnice k2 je bod X2. Přímka x1 prochází bodem X1 a je rovnoběžná s vedlejší osou elipsy o2. Přímka x2 prochází bodem X2 a je rovnoběžná s hlavní osou elipsy o1. Průsečík přímek x1, x2 je bod X. Bod X je bodem elipsy. Volbou bodu X1 na kružnici k1 získáváme různé polohy bodu X na elipse.
V appletu si můžete zkusit, že bod X vykreslí elipsu. Růžovým bodem X1 lze pohybovat.
Applet je vytvořen v programu GeoGebra
Kde je v této konstrukci schovaná osová afinita? Trojúhelníková konstrukce je složena ze dvou osových afinit:
- První pravoúhlá afinita (OA1) je mezi kružnicí k1 (S, a) a elipsou, kde osa afinity je hlavní osa elipsy.
- Druhá pravoúhlá afinita (OA2) je mezi kružnicí k2 (S, b) a elipsou, kde osa afinity je vedlejší osa elipsy.
Bod X1 je obrazem bodu X v OA1. Protože se jedná o pravoúhlou afinitu, bod X leží na přímce x1 kolmé k ose afinity AB procházející bodem X1. Obdobně je bod X2 obrazem bodu X v OA2. Protože se jedná o pravoúhlou afinitu, bod X leží na přímce x2 kolmé k ose afinity CD procházející bodem X2. Průsečík přímek x1, x2 je bod X ležící na elipse.
Důkaz:
Trojúhelníkovou konstrukci lze dokázat podle podobnosti trojúhelníků SX1X* a X2X1X, kde X* je průsečíkem přímky XX1 a osy afinity AB. Přímka X2X je rovnoběžná s osou afinity, proto se rovnají úhly X1X2X, X1SX* a X1XX2, X1X*S. Trojúhelníky SX1X*, X2X1X jsou podobné podle věty uu. V trojúhelnících platí: \(\frac{|XX_1|}{|X_1X^*|}=\frac{|X_2S|}{|X_1S|}=\frac{b}{a}\). Osou afinity je hlavní osa elipsy, směr afinity je kolmý k ose afinity. Je dána osa afinity, směr afinity a charakteristika \(k=\frac{b}{a}\), čímž je OA jednoznačně určena.
Rozdílová proužková konstrukce
Nejprve si ukažme, jak se pomocí rozdílové proužkové konstrukce sestrojí elipsa. (Pozn. Elipsu lze sestrojit i pomocí součtové proužkové konstrukce.)
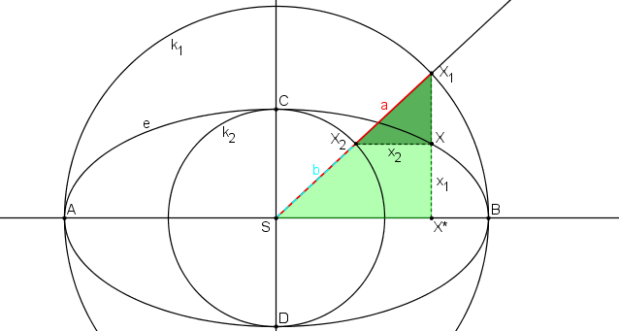
Na rovný proužek papíru vyznačíme body X, Xa, Xb, tak že |XXa|=a, |XXb|=b, |XaXb|=a - b. Nyní pohybujeme proužkem papíru tak, že bod Xa leží vždy na vedlejší ose elipsy (CD) a bod Xb leží na hlavní ose elipsy (AB). Bod X opisuje elipsu, která má velikost hlavní poloosy = a a velikost vedlejší poloosy = b.
Pozn: Proužkové konstrukce využijeme hlavně v případě, pokud máme vyrýsovat elipsu z níž známe hlavní vrcholy A, B a libovolný bod M na elipse.
V appletu si můžeme zkusit, že bod X vykreslí elipsu. Růžovým bodem Xa lze pohybovat.
Applet je vytvořen v programu GeoGebra
Jak se při této konstrukci využívá osová afinita? Bod X sestrojme pomocí trojúhelníkové konstrukce, kde využíváme složení dvou osových afinit. Bodem X vedeme přímku q rovnoběžnou s přímkou SX1. Průsečík přímky q s vedlejší osou elipsy o2 je bod Xa. Úsečky X1X a SXa jsou rovnoběžné a stejně dlouhé. Úsečky SX1 a XaX jsou rovnoběžné. Proto body X1XXaS tvoří rovnoběžník a velikost úsečky XaX = a. Obdobně průsečík přímky q s hlavní osou elipsy o1 je bod Xb. Úsečky X2X a SXb jsou rovnoběžné a stejně dlouhé. Úsečky SX2 a XbX jsou rovnoběžné. Proto body X2XXbS tvoří rovnoběžník a velikost úsečky XbX = b.
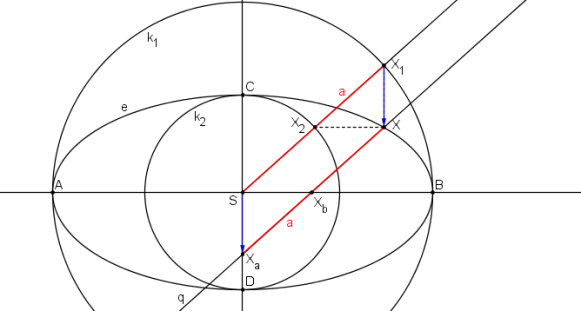
|XaX| = a.
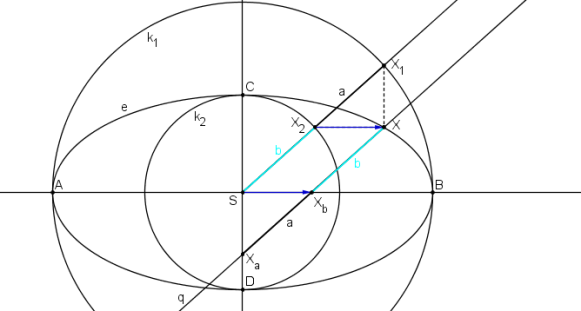
|XbX| = b.

Proužková konstrukce.
Rytzova konstrukce
Z kapitoly o obrazu kružnice v osové afinitě víme, že elipsu můžeme sestrojit pomocí Rytzovy konstrukce. I Rytzovu konstrukci lze odvodit ze vztahu osové afinity mezi kružnicí a elipsou.
Opět vyjdeme z trojúhelníkové konstrukce. Na k1 zvolíme libovolně body K1, L1, M1, N1 tak, že přímky K1L1, M1N1 jsou na sebe kolmé a tvoří tak sdružené průměry kružnice. (Stejně jako přímky K2L2, M2N2.) Pomocí trojúhelníkové konstrukce najdeme body K, L, M, N, které tvoří sdružené průměry elipsy.
Otočme body K, K1, K2 kolem bodu S o 90°. Pak bod K1o splývá s bodem M1 a bod K2o splývá s bodem M2. Body M1, M, M2, Ko tvoří obdélník (M2M || M1 Ko, M2Ko || M1M a úhel M2MM1 je pravý). Bod O je průsečíkem úhlopříček v obdélníku M1, M, M2, Ko. Přímka MKo protíná osy elipsy v bodech 1, 2. Pro |M2|<|M1| platí, že |M2| = b, |M1| = a. |M2| = b plyne z podobnosti trojúhelníků SO2, M1OM. Protože vrchol trojúhelníka O je průsečíkem úhlopříček v obdélníku, úhly při vrcholech M1, M jsou shodné. Úsečky M1M, S2 jsou rovnoběžné. Proto jsou úhly při vrcholech S, 2 také shodné. Proto platí: |SM1| = |M2| = b. Pro velikost |M1| = a platí obdobný vztah, ale vycházíme ze shodnosti trojúhelníků M1OKo, M2OM a podobnosti trojúhelníků SO1, M2OKo. Podobně platí |Ko1| = b, |Ko2| = a. Protože O je průsečíkem úhlopříček obdélníka M1, M, M2, Ko, platí |OM1| = |OM| = |OM1| = |OKo|. Proto platí |O2| = |OS| = |O1|. Body S, 1, 2 proto leží na kružnici se středem v bodě O a poloměrem OS. Při Rytzově konstrukci se využívá této kružnice při hledání bodů 1, 2. Přímky S1, S2 jsou hlavní a vedlejší osa elipsy.
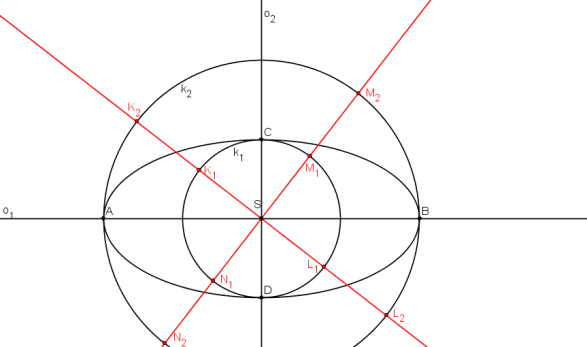
Průměry K1, L1, M1, N1 (resp. K2, L2, M2, N2) jsou na sebe v kružnici k1 (resp. k2) kolmé.
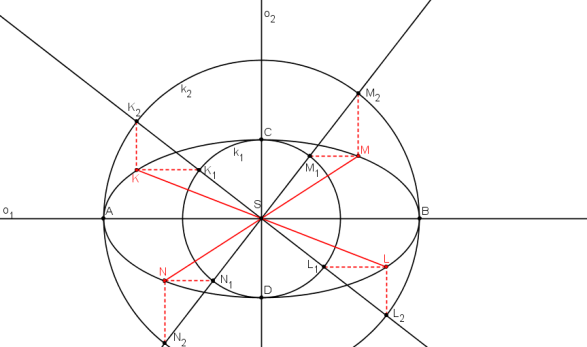
Body K, L, M, N jsou sestrojeny trojúhelníkovou konstrukcí.
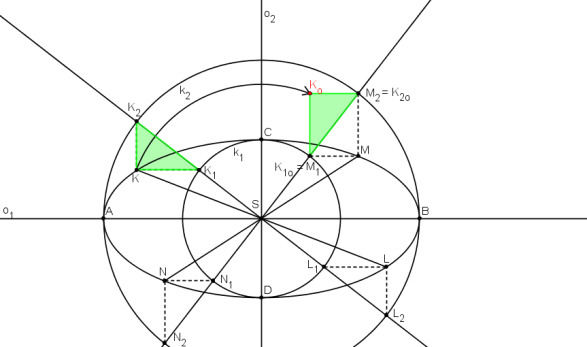
Body KK1K2 otočíme kolem bodu S o 90° tak, že body K1o, M1 a K2o, M2 splývají.

Body M1, M, M2, Ko tvoří obdélník. Bod O je průsečíkem úhlopříček obdélníka.
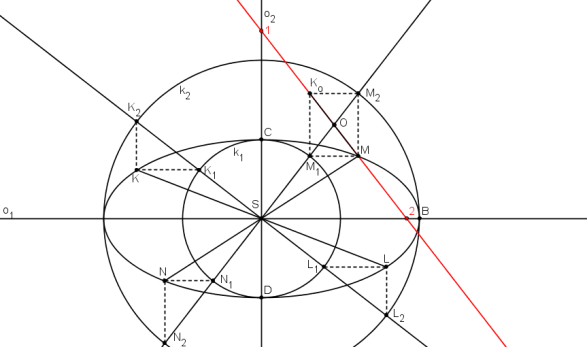
Přímka MKo protíná osy elipsy v bodech 1, 2.
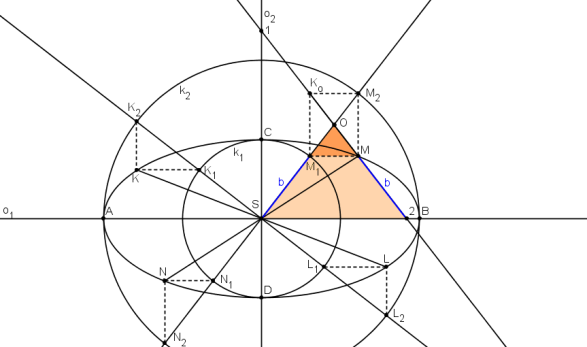
|M2| = b plyne z podobnosti trojúhelníků SO2, M1OM.
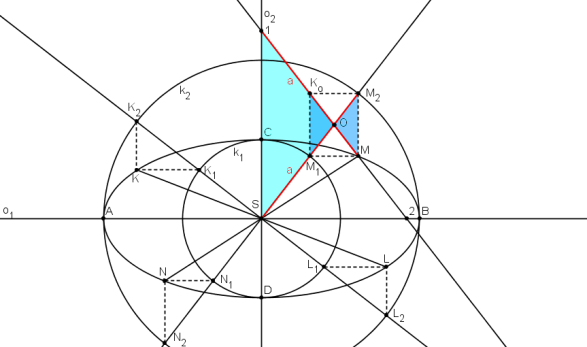
|M1| = a plyne ze shodnosti trojúhelníků M1OKo, M2OM a podobnosti trojúhelníků SO1, M1OKo.
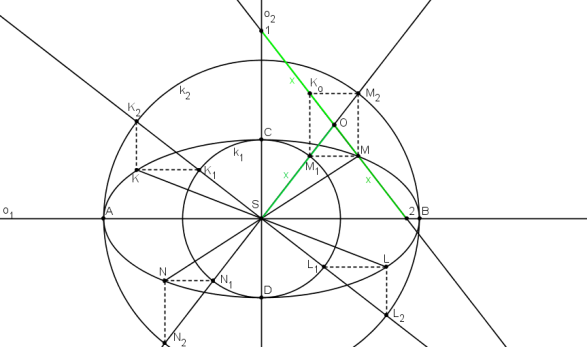
Platí: |O2| = |OS| = |O1|.
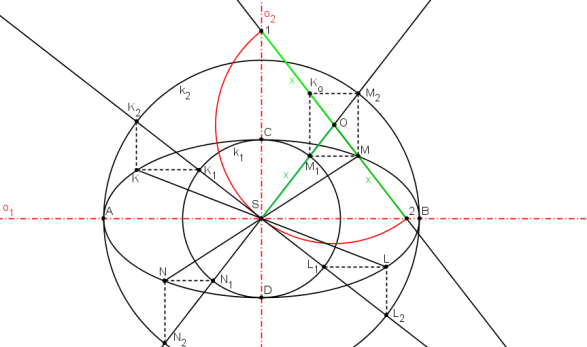
Body S, 1, 2 proto leží na kružnici se středem v bodě O a poloměrem OS.
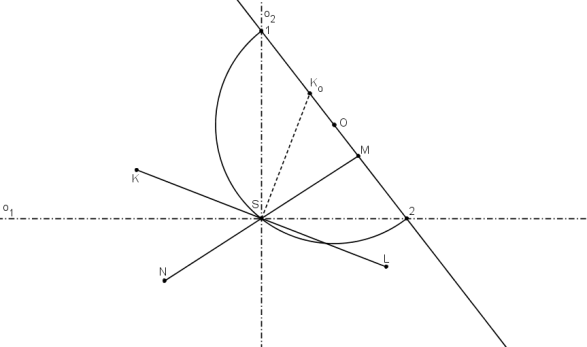
V praxi použijeme tyto prvky.
Součtová proužková konstrukce
Přímo z Rytzovy konstukce vyplývá součtová proužková konstrukce.
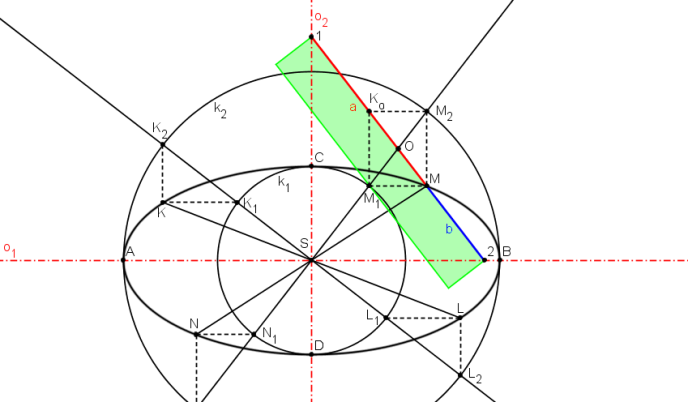
Na rovný proužek papíru vyznačíme body M, Xa, Xb, tak že |MXa|=a, |MXb|=b, |XaXb|= a + b. Nyní pohybujeme proužkem papíru tak, že bod Xa leží na vedlejší ose elipsy o2 a bod Xb leží na hlavní ose elipsy o1. Bod M opisuje elipsu, která má velikost hlavní poloosy je rovna a a velikost vedlejší poloosy je rovna b.
V appletu si můžeme zkusit, že bod M vykreslí elipsu. Růžovým bodem Xb lze pohybovat.
Applet je vytvořen v programu GeoGebra
Příčková konstrukce
K příčkové konstrukci elipsy využijeme bodovou konstrukci kružnice. Úsečky AB, CD jsou dva k
sobě kolmé průměry kružnice k. Bod E je průsečík tečen kružnice v bodech B a C.
Je-li bod U bodem úsečky SC a bod V
bodem úsečky CE, UV || SE, je průsečík X přímek AU a BV bodem kružnice
k
[7].
V appletu si můžete zkusit, že bod X vykresluje kružnici. Růžovým bodem U lze pohybovat.
Applet je vytvořen v programu GeoGebra
Bod V nemusíme vždy hledat pomocí přímky procházející bodem U a rovnoběžné s SE. Můžeme úsečky SC, EC rozdělit na stejný počet dílků a dělicí body očíslovat V1, V2, V3,..., U1, U2, U3,... tak, aby čísla vzrůstala směrem ke společnému bodu úseček, bodu C.
Protože mezi elipsou a kružnicí je vztah osové afinity můžeme tuto konstrukci využít i pro elipsu. Díky zachovávání vlastnosti incidence, rovnoběžnosti a dělicího poměru nemusíme znát hlavní a vedlejší vrcholy, ale libovolné sdružené průměry. Úsečky KL, MN jsou sdružené průměry elipsy e. Úsečky SM, EM rozdělíme na stejný počet dílků (např. čtyři) a dělicí body označíme U1, U2, U3, V1, V2, V3 tak, že čísla vzrůstají směrem ke společnému průsečíku úseček, bodu M. Bod elipsy X1 je průsečíkem přímek KU1, LV1 (X2 je průsečíkem přímek KU2, LV2, X3 je průsečíkem přímek KU3, LV3). Takto jsme vytvořili několik bodů elipsy v jednom kvadrantu. Konstrukci můžeme zopakovat pro ostatní kvadranty.
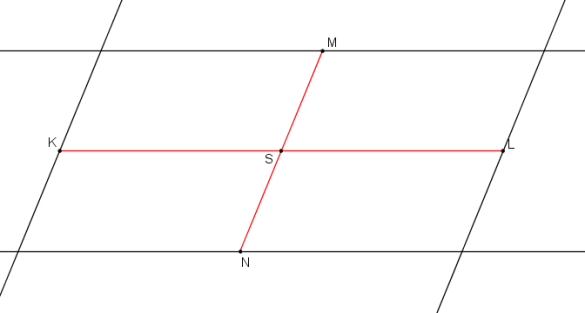
Jsou dány sdružené průměry elipsy KL, MN a tečny v těchto bodech. (Protože KL, MN jsou sdružené průměry, tečny v bodech K, L jsou rovnoběžné s úsečkou MN a tečny v bodech M, N jsou rovnoběžné s úsečkou KL.) Bod E je průsečík tečen elipsy v bodech M, L.

Úsečku SM rozdělíme na 4 díly a dělicí body označíme U1, U2, U3 vzestupně k bodu M. Úsečku EM rozdělíme na 4 díly a body označíme V1, V2, V3 vzestupně k bodu M.
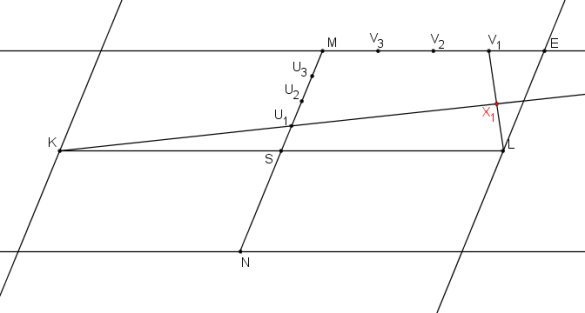
Průsečík přímek KU1, LV1 je bod X1.

Průsečík přímek KU2, LV2 je bod X2.

Průsečík přímek KU3, LV3 je bod X3.
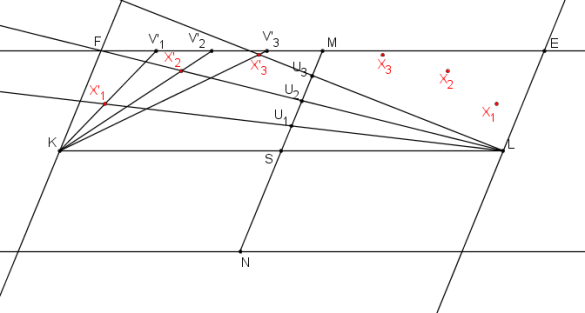
Stejně postupujeme i v rovnoběžníku tvořeném body K, S, M, F.
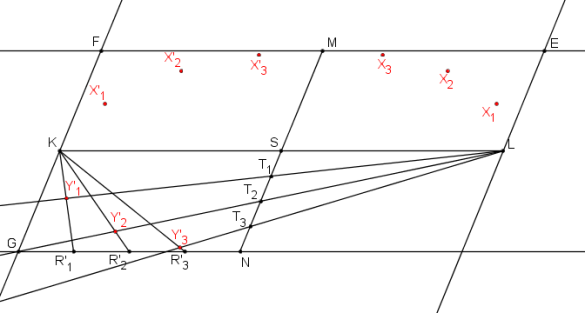
Stejně postupujeme i v rovnoběžníku tvořeném body K, S, N, G.
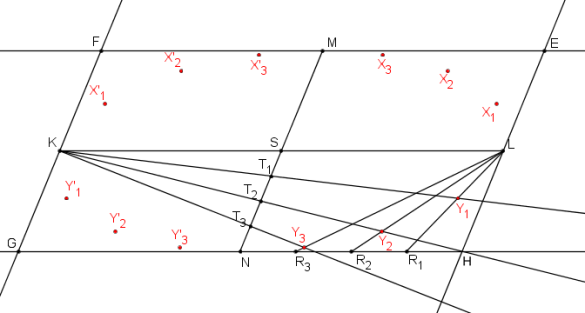
Stejně postupujeme i v rovnoběžníku tvořeném body L, S, N, H.

Nyní máme dostatečný počet bodů pro sestrojení elipsy.
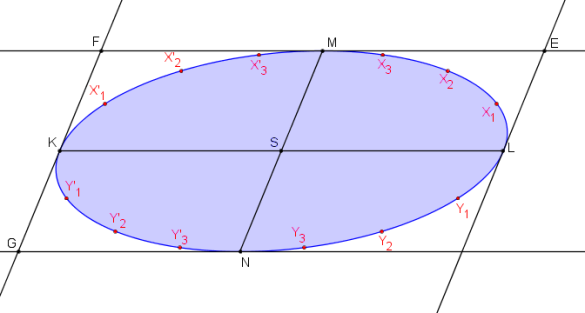
Výsledná elipsa.