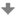Určenost středové kolineace
Středová kolineace určena středem S osou o a párem odpovídajících si bodů A, A´. Pokud je SK zadána takto, můžeme hned konstruovat obrazy prvků. Ne vždy je středová kolineace určena právě takto a proto musíme S, o, A, A´ nejprve určit. Následují příklady o tom, jak může být středová kolineace zadána a řešení, jak najít střed kolineace osu kolineace a pár odpovídajících si bodů.
- Střed kolinace, samodružný bod na ose kolineace a pár odpovídajících si přímek
- Tři páry odpovídajících si bodů
- Osa kolineace a dva páry odpovídajících si bodů
- Střed kolineace a dva páry odpovídajících si přímek
- Střed kolineace, osa kolineace a úběžník
- Střed kolineace, osa kolineace a úběžnice
- Osa kolineace, pár odpovídajících si přímek a odpovídající si body, které na přímce neleží.
- Střed kolineace, osa kolineace a protiúběžník
- Střed kolineace, osa kolineace a protiúběžnice
- Dva páry odpovídajících si přímek takových, že obrazy přímek jsou rovnoběžné a pár odpovídajících si bodů ležící na jedné z nich
Úlohu si nejprve zkuste provést sami: Zadání, Řešení. V řešení se používají jednotné barvy. Zadané prvky modrou barvou, hledané prvky červenou barvou.
Střed kolineace S, samodružný bod X na ose kolineace o a pár odpovídajících si přímek a, a´.
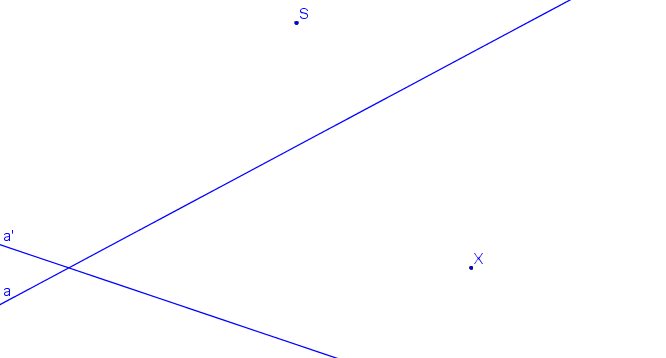
Krokované řešení: SK (S, o, a, a´, X).
Průsečík přímek a, a´ je samodružný bod Y. Samodružné body X, Y určují osu kolineace o. Pár odpovídajících si bodů získáme tak, že středem kolineace S vedeme libovolnou přímku, která protíná přímku a (resp. a´) v bodě A (resp. A´).
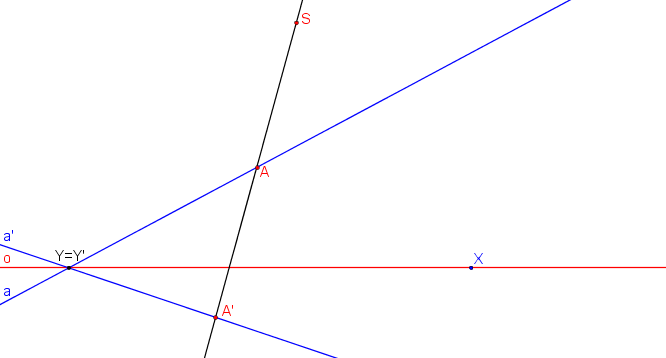
Osa kolineace o a dva páry odpovídajících si bodů A, A´; B, B´.
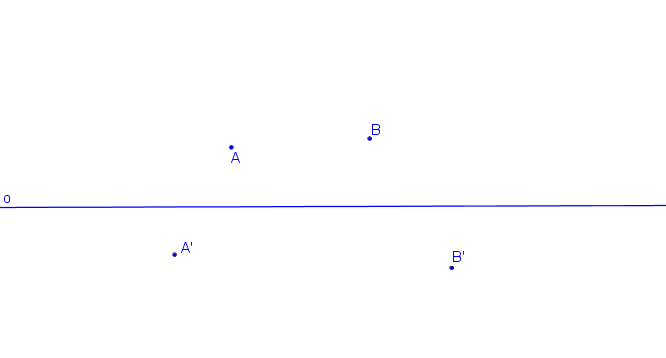
Krokované řešení: SK (o, A, A´; B, B´).
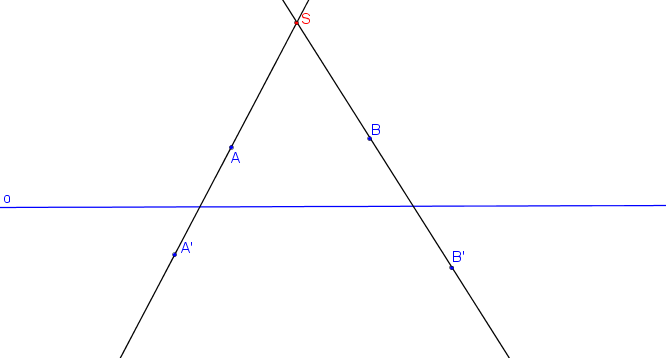
Průsečík přímek AA´, BB´ je střed kolineace S.
Tři páry odpovídajících si bodů A, A´; B, B´; C, C´.
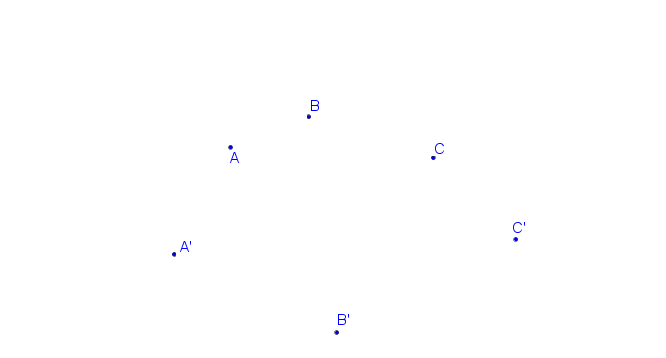
Krokované řešení: SK je dána A, A´, B, B´, C, C´.
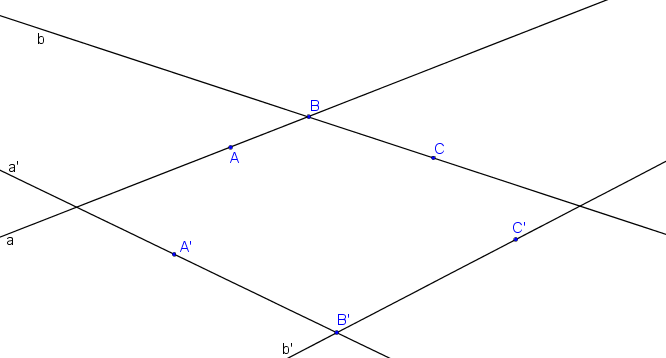
Body AB (resp. BC) určují přímku a (resp. b). Přímku a´ (resp. b´) určují body A´B´ (resp. B´C´).
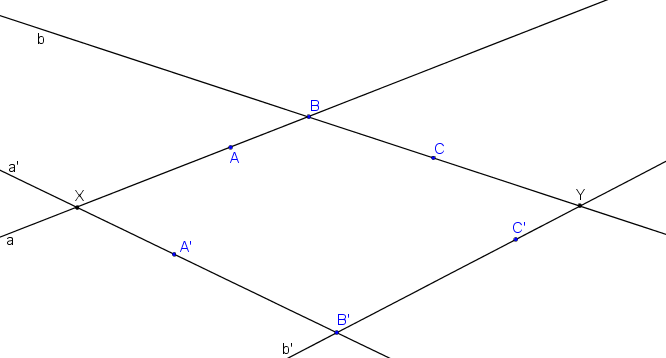
Průsečík odpovídajících si přímek a, a´ (resp. b, b´) je samodružný bod X (resp. Y).
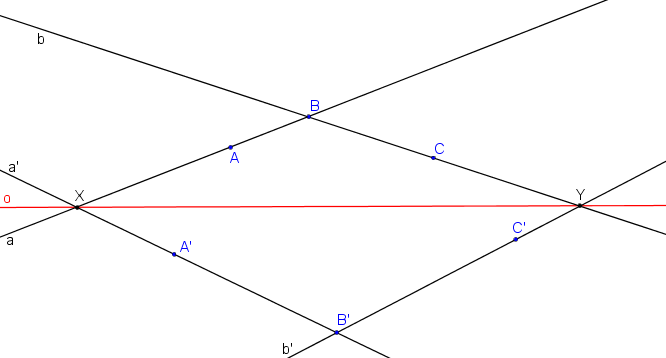
Samodružné body X, Y určují osu kolineace o.
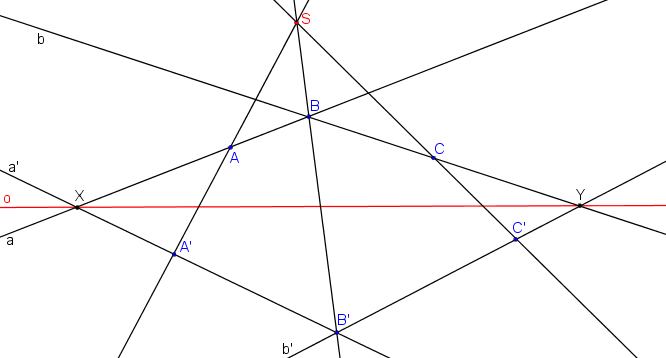
Střed kolineace je průsečíkem přímek AA´, BB´, CC´. (Pokud by se tyto přímky neprotínaly v jednom bodě, není mezi body a přímkami vztah osové afinity.)
Střed kolineace S a dva páry odpovídajících si přímek a, a´; b, b´.
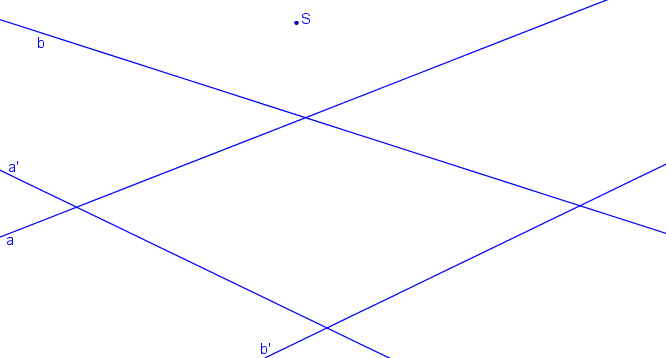
Krokované řešení: SK (S, a, a´; b, b´).
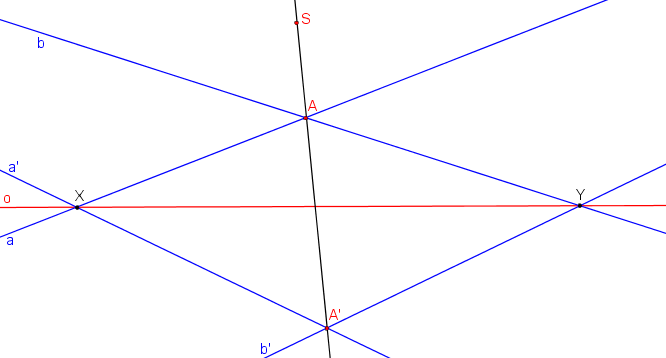
Průsečík přímek a, a´ (resp. b, b´) je samodružný bod X (resp. Y). Samodružné body X, Y určují osu kolineace o. Odpovídající si body jsou body A, A´. Bod A je průsečíkem přímek a, b. Bod A´ je průsečíkem přímek a´, b´. (Pozn. Pokud přímka AA´ neprochází středem kolineace S, nejedná se o středovou kolineaci.)
Střed kolineace S, osa kolineace o a úběžník U.
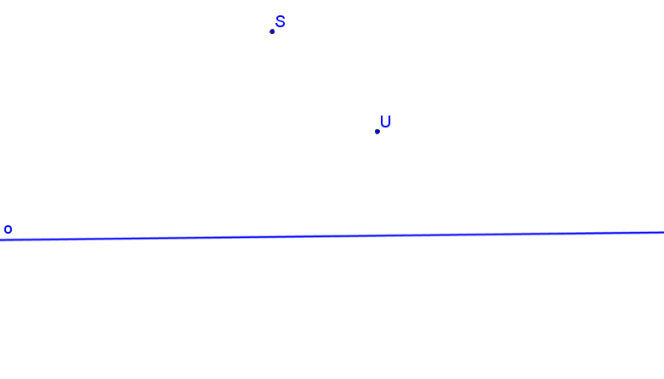
Krokované řešení: SK je dána S, o, U.

Obraz bodu U je nevlastní bod U´∞.

Přímka a je libovolná přímka procházející úběžníkem U.

Přímka a´ prochází samodružným bodem přímky a a je rovnoběžná s přímkou SU (viz Jak najít úběžnici).
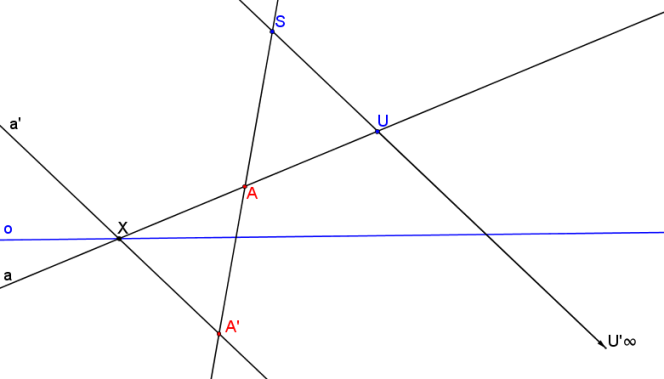
Na přímce a zvolíme libovolný bod A. Bod A´ je průsečík přímek a´, SA.
Střed kolineace S, osa kolineace o a úběžnice u.
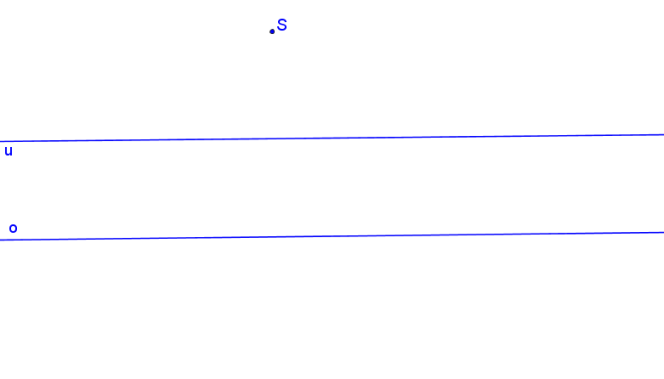
Krokované řešení: SK (S, o, u).
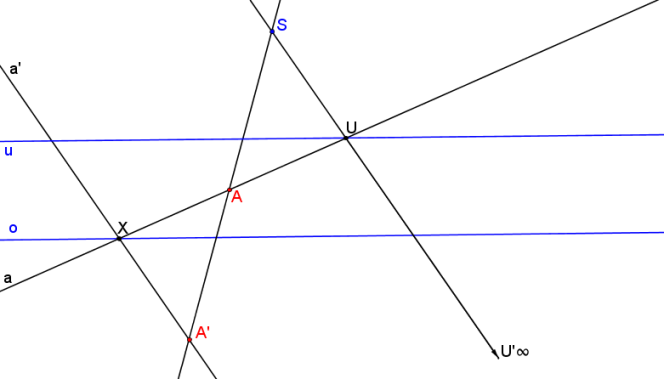
Na úběžnici u libovolně zvolíme úběžník U a postupujeme stejně jako v předchozím příkladě: Je dáno S, o, U.
Osa kolineace o, pár odpovídajících si přímek a, a´ a odpovídající si body P, P´, které na přímce p neleží.
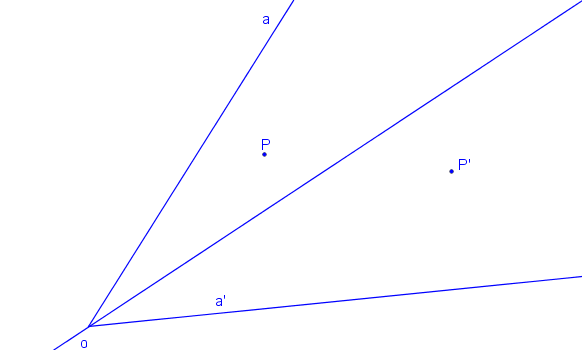
Krokované řešení: SK (o, a, a´, P, P´).
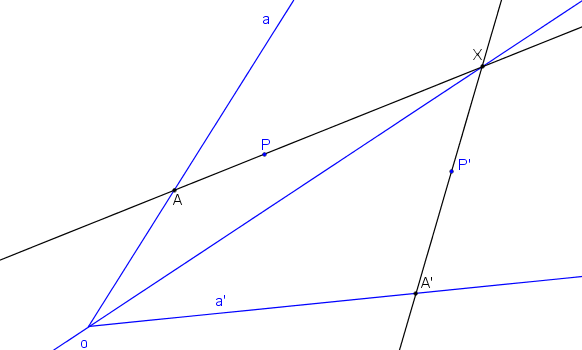
Na přímce a libovolně zvolíme bod A a pomocí bodu P určíme jeho obraz A´. A´ je průsečík přímek a´, XP´.
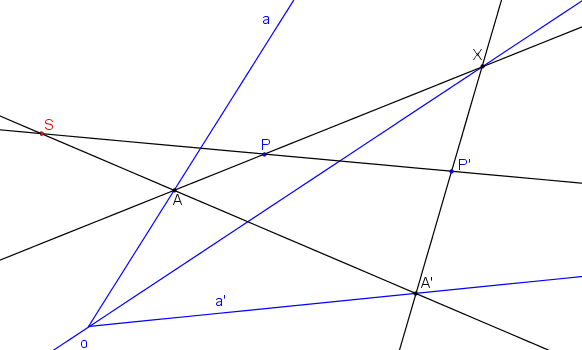
Střed kolineace S je průsečíkem přímek AA´, PP´.
Střed kolineace S, osa kolineace o a protiúběžník V´.
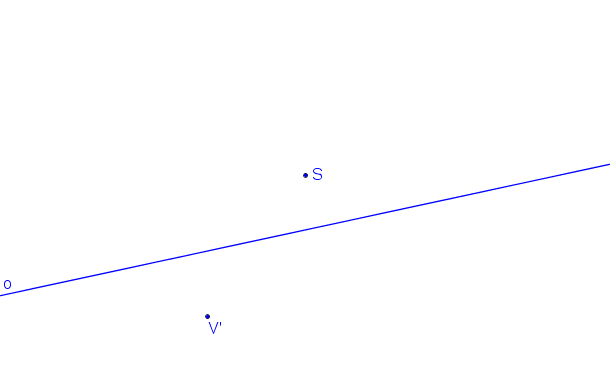
Krokované řešení: SK (S, o, V´).
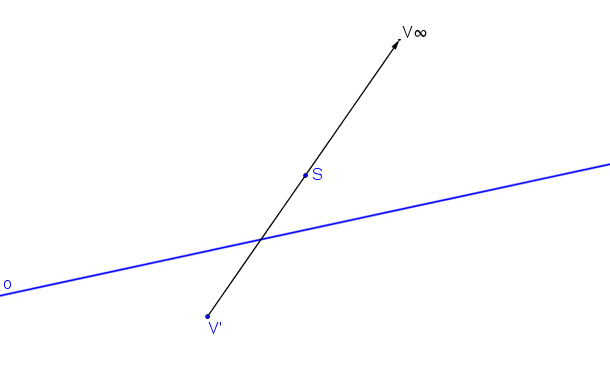
Obraz bodu V´ je nevlastní bod V∞.
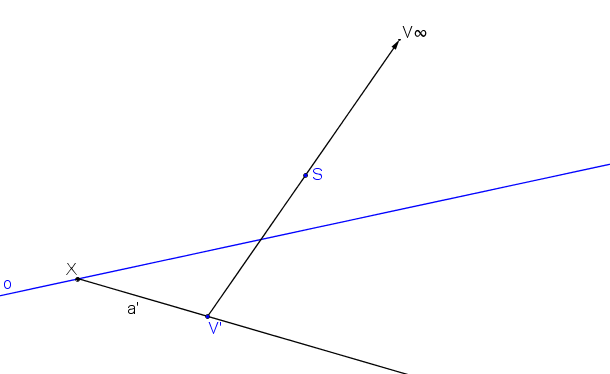
Přímka a´ je libovolná přímka procházející protiúběžníkem V´.
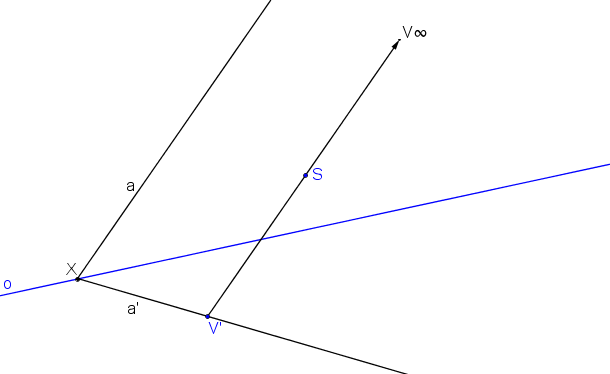
Přímka a prochází samodružným bodem přímky a´ a je rovnoběžná s přímkou SV´ (viz Jak najít úběžnici).

Na přímce a zvolíme libovolný bod A. Bod A´ je průsečík přímek a´, SA.
Střed kolineace S, osa kolineace o a protiúběžnice v´.
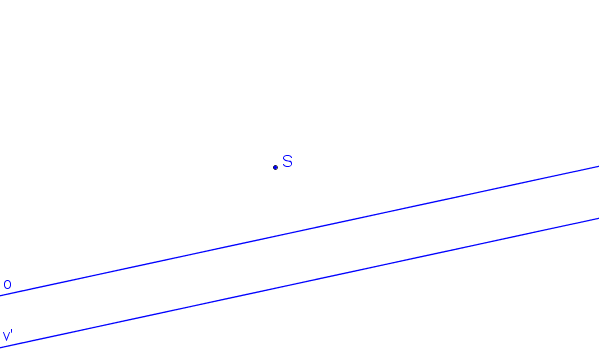
Krokované řešení: SK (S, o, v´).
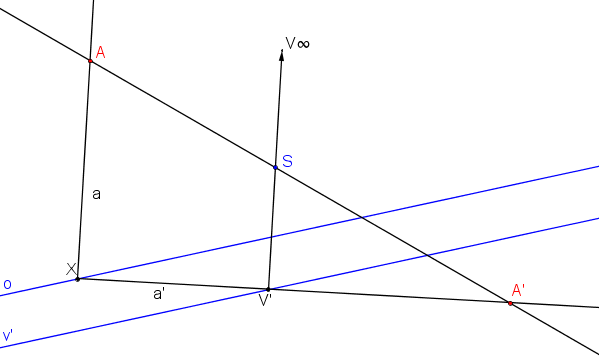
Na protiúběžnici v´ libovolně zvolíme protiúběžník V´ a postupujeme stejně jako v předchozím příkladě: Je dáno S, o, v´.
Dva páry odpovídajících si přímek p, p´; q, q´ takových, že přímky p´, q´ jsou rovnoběžné a pár odpovídajících si bodů P, P´ ležící na jedné z přímek.
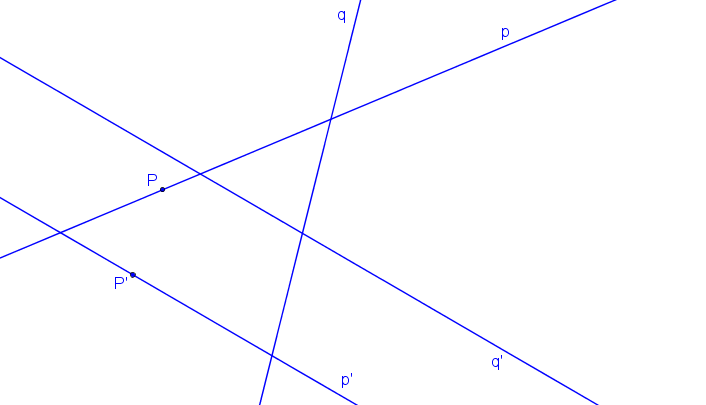
Krokované řešení: SK (p, p´, P, P´; q, q´).
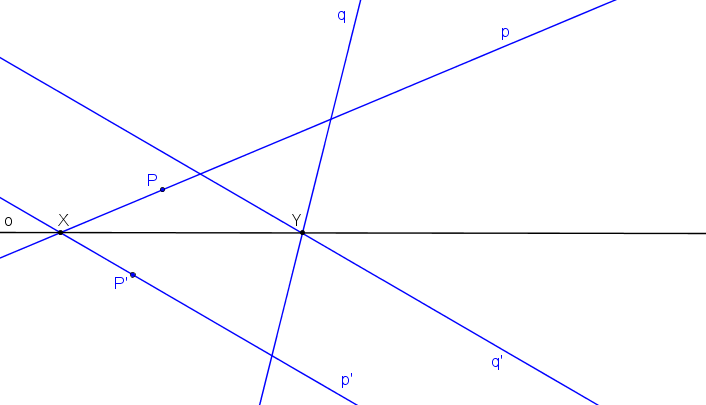
Průsečíky přímek p, p´ (q, q´) jsou samodružné body X, Y určující osu kolineace o.
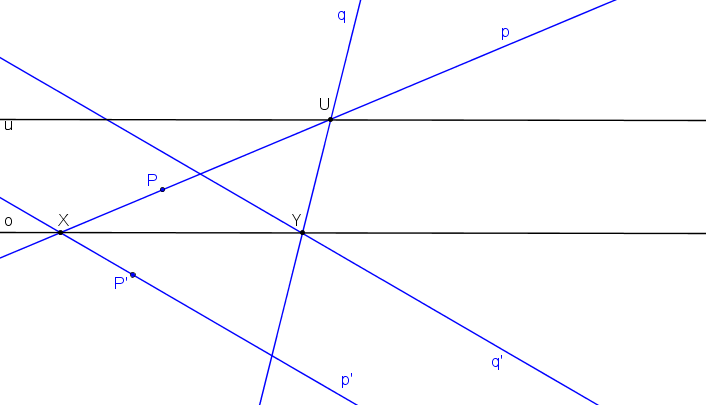
Průsečík přímek p, q je úběžník U, protože se přímky p, q zobrazí jako rovnoběžky. Úběžnice u prochází úběžníkem U a je rovnoběžná s osou kolineace o.
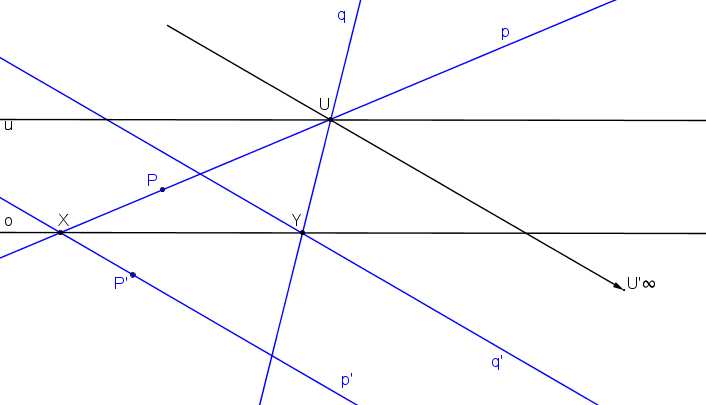
Nevlastní bod U´∞ leží na přímce rovnoběžné s přímkami p´, q´ procházející bodem U.
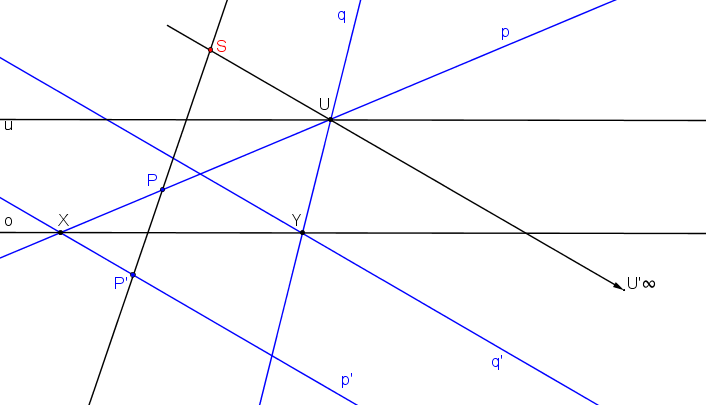
Střed kolineace S je průsečíkem přímek PP´, UU´∞.