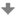\begin{align} \end{align}

Konstrukce kuželoseček

Díky tomu, že obrazem kružnice ve středové kolineaci je elipsa, parabola i hyperbola, můžeme středovou kolineaci využít při řešení úloh o kuželosečkách. K úlohám jsou však často potřeba znalosti projektivní geometrie, kterými se tato práce nezabývá a většina konstrukcí je nad rámec středoškolského učiva. Uveďme si tedy pouze několik příkladů, ve kterých můžeme SK použít. U příkladů najdete literaturu, kde můžete najít řešení.

Středová kolineace mezi kružnicí a kuželosečkou se užívá při konstrukci kuželosečky dané body a tečnami. Vždy je potřeba pět určujících prvků (nebo čtyři prvky + typ kuželosečky).

  • Příklad: Sestrojte rovnoosou hyperbolu, je-li dán směr M∞ jedné asymptoty, tečna t s dotykovým bodem T a bod C.

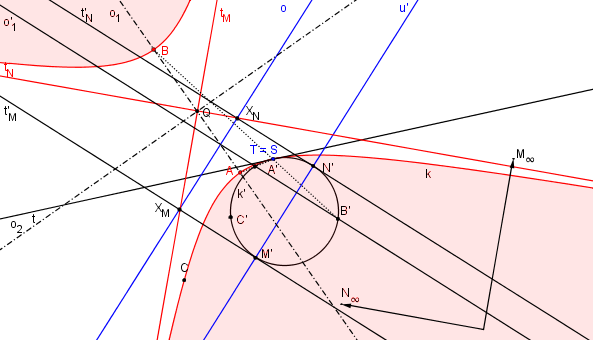
    Řešení: Střed kolineace S zvolíme v dotykovém bodě T tečny t a kružnici k´ tak, aby se dotýkala tečny t v bodě T. K bodům C, M∞, N∞ (směr N∞ je kolmý ke směru M∞, protože hyperbola má být rovnoosá) najdeme odpovídající body C´, M´, N´. Úběžnice je přímka u´ = M´N´. Osa kolineace o je rovnoběžná s u´ a prochází průsečíkem přímek CN∞, C´N´ 

    — Urban A.: Deskriptivní geometrie I  [10] (str. 387).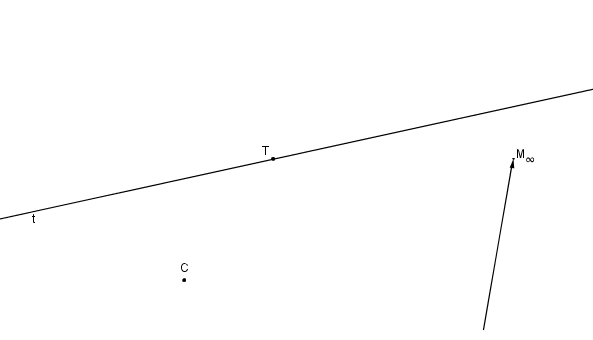

    Tímto jsme našli kolineaci, která převádí kružnici k´ na hledanou hyperbolu. K sestrojení hyperboly využijeme postup popsaný v kapitole SK Obraz kružnice.

    Krokované řešení: Sestrojte rovnoosou hyperbolu, je-li dán směr M∞ jedné asymptoty, tečna t s dotykovým bodem T a bod C.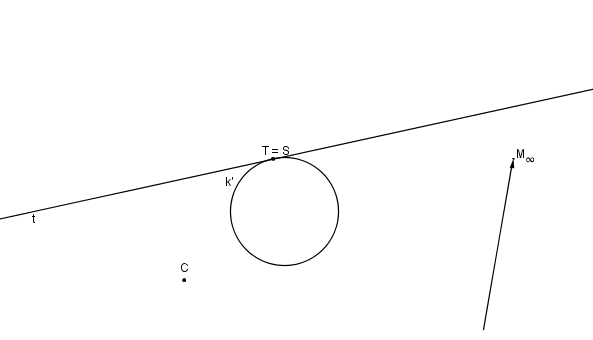

    Střed kolineace S zvolíme v dotykovém bodě T tečny t a kružnici k´ tak, aby se dotýkala tečny t v bodě T.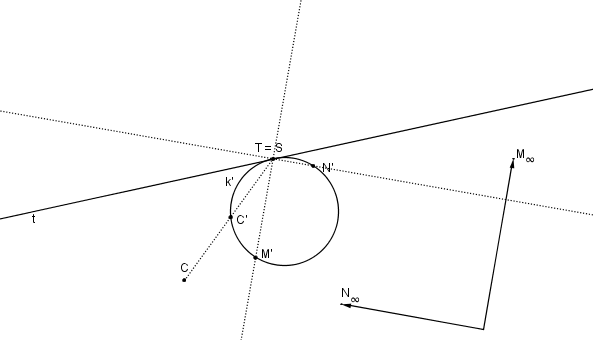

    K bodům C, M∞, N∞ (směr N∞ je kolmý ke směru M∞, protože hyperbola má být rovnoosá) najdeme odpovídající body C´, M´, N´.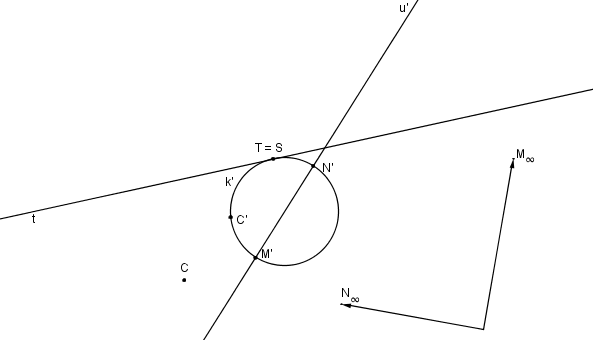

    Úběžnice je přímka u´ = M´N´.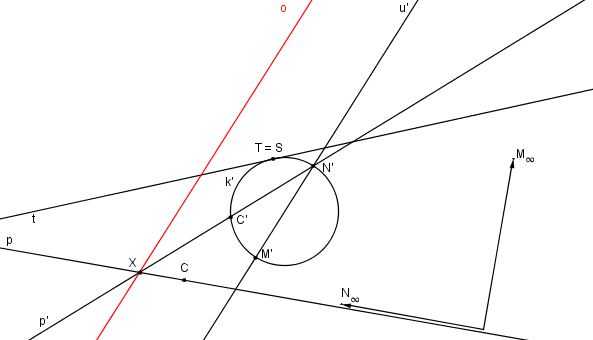

    Bod X je průsečíkem přímek CN∞, C´N´. Osa kolineace o je rovnoběžná s u´ a prochází samodružným bodem X.

    Tímto jsme našli SK (S, o, u), která převádí kružnici k´ na hledanou hyperbolu.

    K sestrojení hyperboly využijeme postup popsaný v kapitole SK Obraz kružnice.
  • Kuželosečka je dána dvěma tečnami a, b s body dotyku A, B a dalším bodem C. Sestrojte další bod [10] (str. 384).
  • Sestrojte parabolu, jsou-li dány dva její body A, B a tečny c, d [10] (str. 386).
  • Sestrojte hyperbolu, je-li dána její asymptota m a tři body A, B, C [10] (str. 386).
  • Sestrojte rovnoosou hyperbolu, která je dána tečnou t s bodem dotyku T a dvěma body M1, M2 [5] (str. 51).
  • Sestrojte kuželosečku, jsou-li dána tři její body A, B, C a ohnisko F [2] (str. 202).
  • Sestrojte kuželosečku, jsou-li dány tři její body a dvě tečny [2] (str. 201).
  • Sestrojte kuželosečku, jsou-li dány dva její body a tři tečny [2] (str. 202).