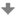Úběžníky a úběžnice
Ve středové kolineaci je ještě jedna námi zatím neprobádaná oblast, na kterou se společně podíváme právě v této kapitole.
Vraťme se ke středové kolineaci jako ke vztahu mezi dvěma rovinami. Možná vás napadlo se zeptat, co se stane, když bude bod A v takové poloze, že přímka SA neprotne rovinu β´. Kde je potom obraz bodu A´? Průsečík přímky SA a roviny β´ je nevlastní bod A´∞. Vlastní bod, který se zobrazí na nevlastní bod je tzv. úběžník, obvykle jej značíme U.
Pojďme si představu o úběžníku rozšířit. Bodem S můžeme vést nekonečně mnoho přímek rovnoběžných s rovinou β´. Tyto přímky vyplní celou rovinu α rovnoběžnou s rovinou β´. Jak již víme, průsečnice rovnoběžných rovin je tzv. nevlastní přímka. Přímka, která se zobrazí na nevlastní přímku je tzv. úběžnice, obvykle ji značíme u. Úběžnicí je průsečnice roviny β s rovinou α.

Krokované řešení: Bod U leží v takové poloze, že přímka SU je s rovinou β´ rovnoběžná. Bod U´∞ je nevlastní bod přímky SU. Vlastní bod U, který se zobrazí na nevlastní bod U´∞ - úběžník.

Bod A leží v takové poloze, že přímka SA je s rovinou β´ rovnoběžná. Bod A´∞ je nevlastní bod přímky SA.

Středem kolineace S proložíme rovinu α rovnoběžnou s β´. Jejich průsečnice je nevlastní přímka. Vlastní přímka u se zobrazí na nevlastní přímku - úběžnice.
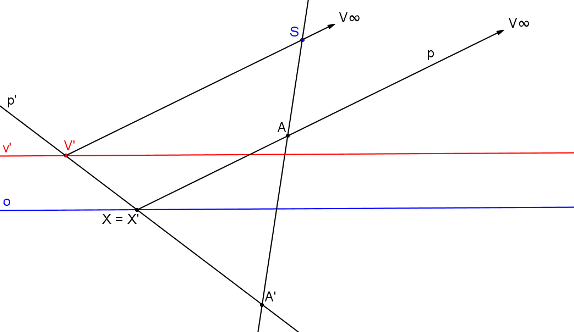
Na problém se můžeme dívat i obráceně. Bod A´ leží v rovině β´ tak, že přímka SA´ neprotne rovinu β. Průsečík přímky SA´ a roviny β je nevlastní bod A∞. Nevlastní bod, který se zobrazí na vlastní je tzv. protiúběžník, obvykle jej značíme V´.
Úvahu můžeme opět rozšířit tak, že bodem S proložíme rovinu δ, rovnoběžnou s rovinou β. Nevlastní přímka, která se zobrazí na vlastní přímku je tzv. protiúběžnice, obvykle ji značíme v´. Protiúběžnice je průsečnice rovnoběžných rovin δ a β´. (Pozn: V některých literaturách je protiúběžnice označena jako úběžnice a protiúběžník pouze jako úběžník.)

Krokované řešení: Bod U´ leží v takové poloze, že přímka SU´ je s rovinou β rovnoběžná. Bod U∞ je nevlastní bod přímky SU´. Nevlastní bod U∞ se zobrazí na vlastní bod U´ - protiúběžník.
Bod A´ leží v takové poloze, že přímka SA´ je s rovinou β rovnoběžná. Bod A∞ je nevlastní bod přímky SA´.

Středem kolineace S lze sestrojit rovinu δ rovnoběžnou s β. Jejich průsečnice je nevlastní přímka v´. Nevlastní přímka v se zobrazí na vlastní přímku v´ - protiúběžnice.
Středovou kolineaci používáme častěji jako vztah v rovině. Stejně jako jsme převedli vztah středové kolineace mezi dvěma rovinami do roviny, najdeme i průměty úběžnice. Prvky převedeme do roviny π pomocí rovnoběžného promítání. V prostoru jsou úběžnice (protiúběžnice) s osou kolineace rovnoběžné. Protože rovnoběžné promítání zachovává rovnoběžnost tak i průmět úběžnice (protiúběžnice) je s průmětem osy kolineace rovnoběžný. Stačí proto najít jeden úběžník U (protiúběžník V´). Úběžnice u (v´) prochází bodem U (V´) a je rovnoběžná s osou kolineace o.
Nalezení úběžnice
Středová kolineace v rovině je dána středem kolineace S, osou kolineace o a párem odpovídajících si bodů A, A´. Jak najdeme úběžnici? Zvolíme si libovolnou přímku p procházející bodem A, která neprochází středem S a není rovnoběžná s osou o, a najdeme její obraz p´. Hledáme bod U přímky p, který se zobrazí na nevlastní bod U´∞. U´∞ je určen směrem přímky p´. Pro body UU´∞ (stejně jako pro libovolné dvojice odpovídajících si bodů) platí, že leží na přímce procházející středem kolineace S. Přímka q, na které leží body UU´∞, proto prochází středem kolineace S. Bod U´∞ leží ve směru přímky p´, proto je přímka q rovnoběžná s přímkou p´. Bod U leží na spojnici SU´∞ (přímce q) a zároveň na přímce p. U = p ∩ q. Nyní známe jeden úběžník U. Z předchozího odstavce víme, že úběžnice a osa kolineace jsou vzájemně rovnoběžné. Úběžnice u je proto rovnoběžná s osou kolineace o a prochází úběžníkem U.

Krokované řešení: SK je dána S, o, A, A´.

Přímka p je libovolná přímka procházející bodem A. p´ je její obraz.
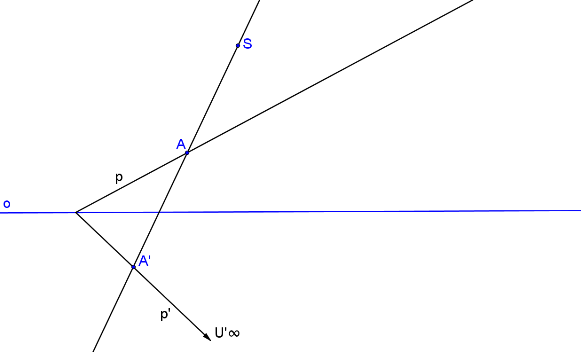
Bod U´∞ je nevlastní bod přímky p´.
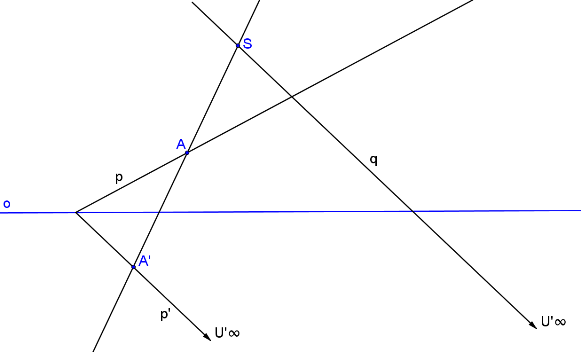
Body UU´∞ jsou odpovídající si body - leží na přímce q, která prochází středem S a je rovnoběžná s přímkou p´.

Průsečík přímek p, q je hledaný bod U.

Úběžnice u je rovnoběžná s osou kolineace o a prochází úběžníkem U.
Můžete se přesvědčit, že postup nezávisí na volbě přímky p. S růžovým bodem C lze pohybovat.
Applet je vytvořen v programu GeoGebra
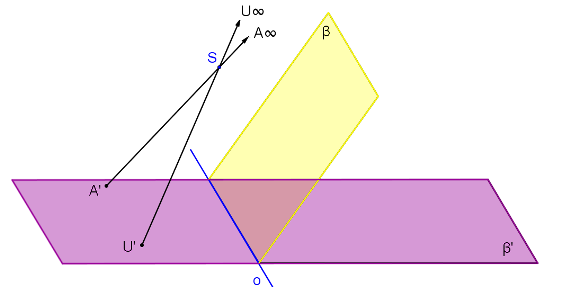
Obdobně nalezneme protiúběžnici. Zvolíme si libovolnou přímku p procházející bodem A, která neprochází středem S a není rovnoběžná s osou o, a najdeme její obraz p´. Hledáme bod V´ přímky p´, který se zobrazí na nevlastní bod V∞. V∞ je určen směrem přímky p. Body V, V´, S leží na jedné přímce, označme ji q. Bod V∞ leží ve směru přímky p. Přímka q proto rovnoběžná s přímkou p a zároveň prochází středem kolineace S. Bod V´ leží na spojnici SV∞ (přímce q) a zároveň na přímce p´. V´ = p´ ∩ q. Nyní známe jeden protiúběžník V´. Protiúběžnice v´ je rovnoběžná s osou kolineace o a prochází protiúběžníkem V´.