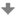Řezy jehlanů
V kapitole budeme pracovat s tělesy, která jsou zobrazena ve volném rovnoběžném promítání
Jehlan, jehlanový prostor a jehlanová plocha
Než začneme pracovat s jehlany, připomeňme definici jehlanové plochy a jehlanového prostrou.
Množina všech přímek procházejících daným bodem V a protínajících mnohoúhelník m (jeho obvod),
který leží v rovině φ neprocházející bodem V, se nazývá jehlanový prostor
(jehlanová plocha)
[10] (str. 90). Bod V se
nazývá vrchol. Množina všech přímek plochy, které protínají stranu mnohoúhelníka m, tvoří
stěnu jehlanové plochy. Je-li mnohoúhelníkem n-úhelník, mluvíme o n-boké jehlanové ploše.
Jehlan získáme z jehlanového prostrou tak, že jej omezíme dvěma rovinami. Jednou rovinou je zpravidla rovina φ a mnohoúhelník m pak nazýváme podstavou jehlanu. Druhou rovinou je rovina φ´ (φ´||φ) procházející vrcholem V. Vzdálenost rovin φ, φ´ se nazývá výška jehlanu. Má-li podstava střed S a platí, že přímka SV je kolmá k rovině φ, pak se jehlan nazývá kolmý, jinak je kosý. Je-li jehlan kolmý a jeho podstavu (mnohoúhelník m) tvoří pravidelný n-úhelník, pak se jehlan nazývá pravidelný.
Můžeme se setkat ještě s jedním typem jehlanu - komolý jehlan. Komolý jehlan získáme z jehlanové plochy tak, že ji omezíme dvěma rovinami. Jednou rovinou je zpravidla rovina φ. Druhou rovinou je rovina φ´ (φ´||φ), která však neprochází vrcholem V a vzdálenost rovin φ, φ´ je menší než výška jehlanu.
Řezy jehlanů
Jak již víme z úvodu kapitoly SK mezi dvěma rovinami, středovou kolineaci lze využít při řezu jehlanu rovinou. Hrany AV, BV,... prochází společným bodem V. Vrchol V je proto zároveň střed kolineace S. Osu kolineace tvoří průsečnice roviny podstavy a roviny řezu. Odpovídající si body jsou body A, A´, kde bod A´ je bodem hrany AV a zároveň leží v rovině řezu a bod A je bodem hrany AV a zároveň leží v rovině podstavy.
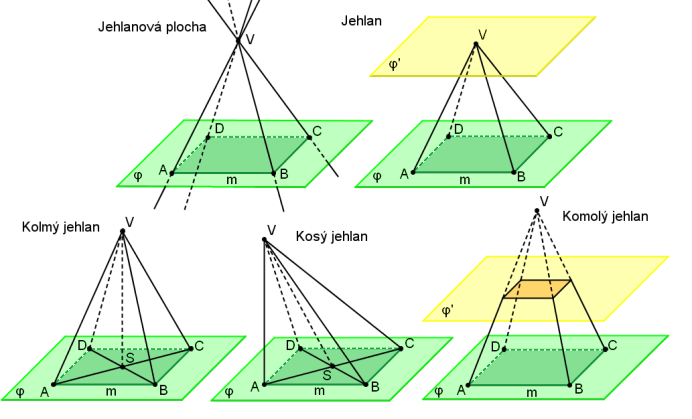
Příklad: Je dán pravidelný šestiboký jehlan s podstavou ABCDEF. Rovina řezu je dána průsečnicí o roviny řezu a roviny podstavy a bodem A´, který leží na hraně AV.

Krokované řešení: Je dán šestiboký jehlan s podstavou ABCDEF. Rovina řezu je určena přímkou o a bodem A´.
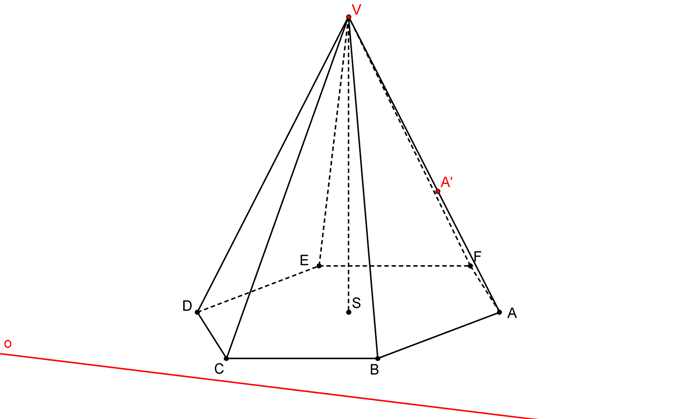
SK je dána S = V, o, AA´. Postupně nalezneme body řezu na hranách jehlanu jako obrazy vrcholů podstavy ve SK.
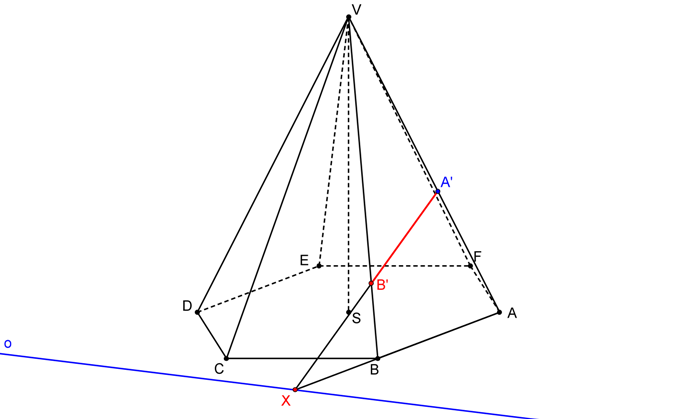
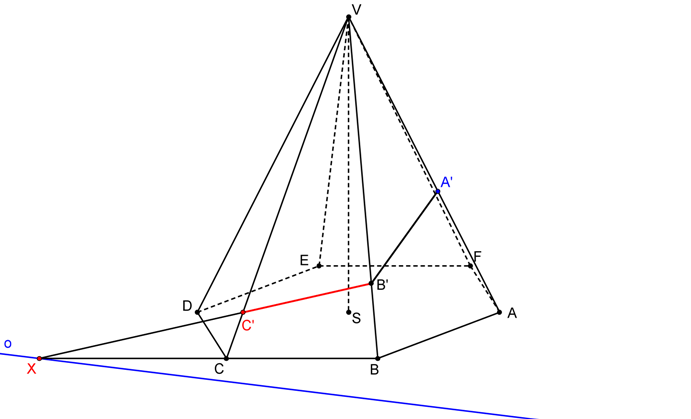
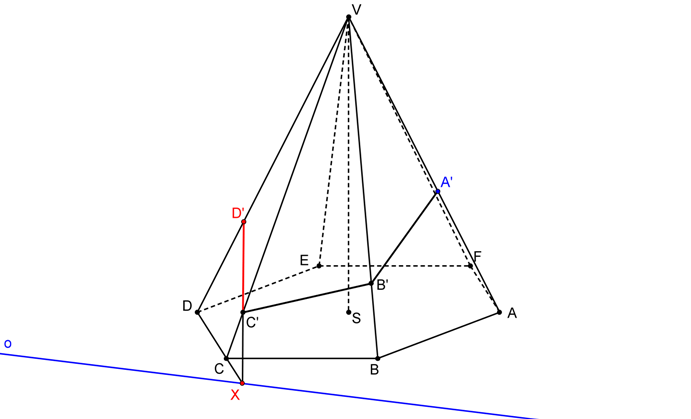
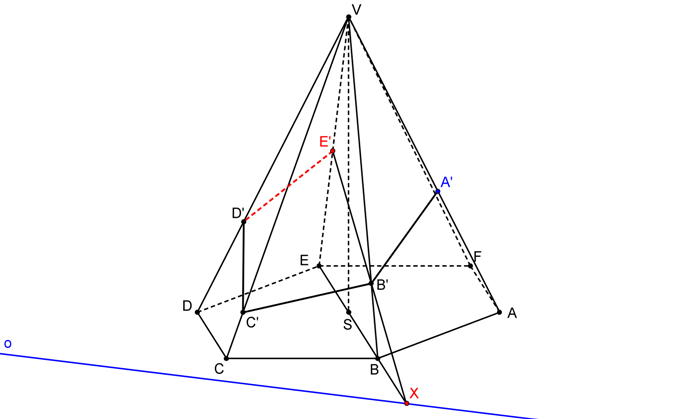
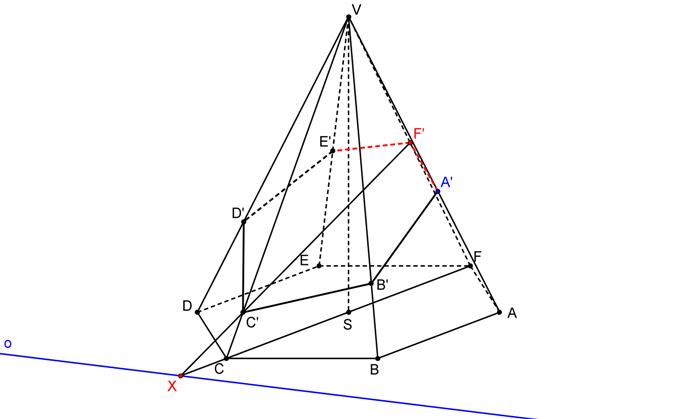
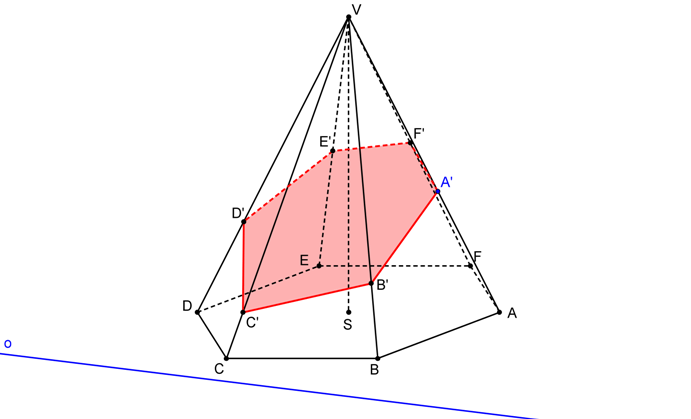
Řezem je šestiúhelník A´B´C´D´E´F´.
Postupujeme stejně, pokud je úkolem sestrojit řez kosého jehlanu.
Příklad: Mějme dán kosý čtyřboký jehlan ABCDV. Rovina řezu α je určena bodem X´ a přímkou p´. Bod X´ leží v rovině řezu a zároveň v rovině podstavy. Dále je dána přímka p, která je průmětem přímky p´ do roviny podstavy z bodu V .
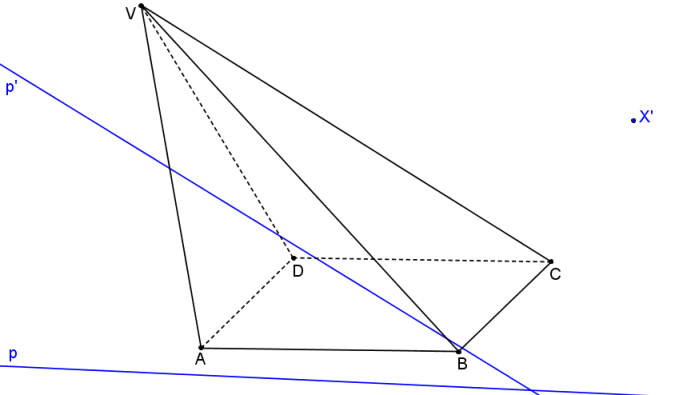
Krokované řešení: Je dán kosý čtyřboký jehlan s podstavou ABCD. Rovina řezu α je určena bodem X´ a přímkou p´. Bod X´ leží v rovině řezu a zároveň v rovině podstavy. Dále je dána přímka p, která je průmětem přímky p´ do roviny podstavy z bodu V
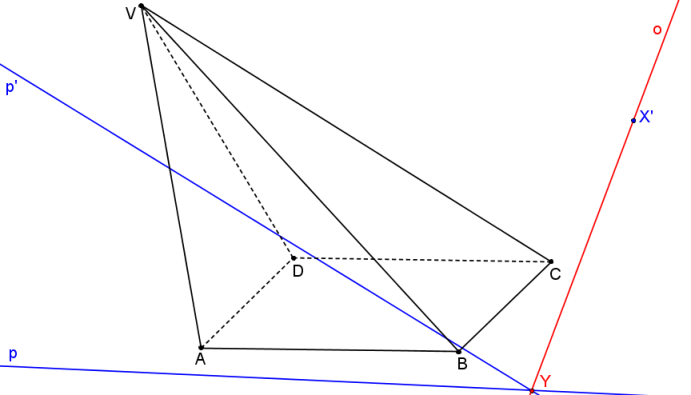
Osa kolineace o prochází samodružným bodem X´ a průsečíkem (samodružným bodem) přímek p, p´.
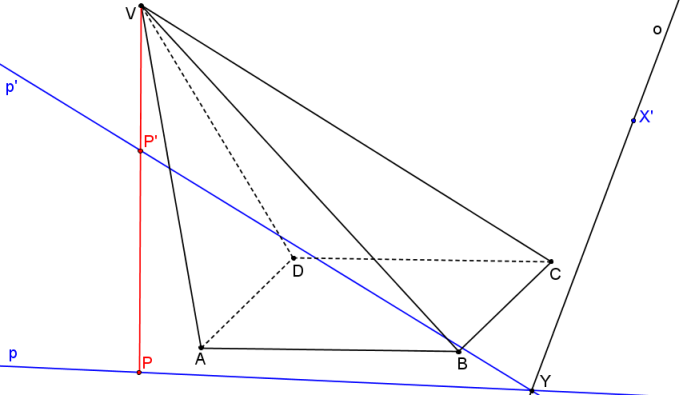
Nyní stačí na přímkách p, p´ určit body P, P´ tak, aby platilo, že přímka PP´ prochází vrcholem V.
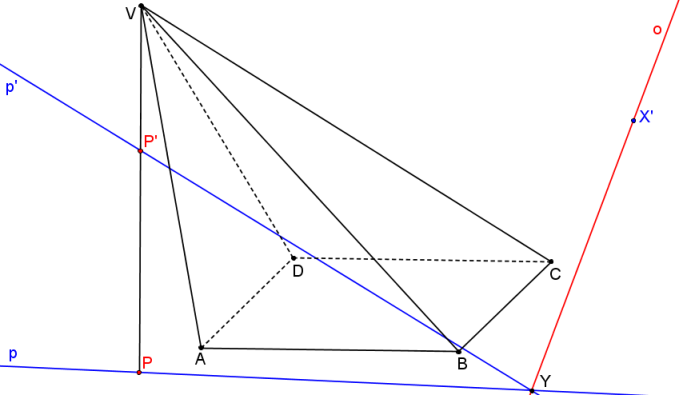
Nyní je dána SK (S = V, o, PP´). Postupně nalezneme body řezu na hranách jehlanu jako obrazy vrcholů podstavy ve SK.
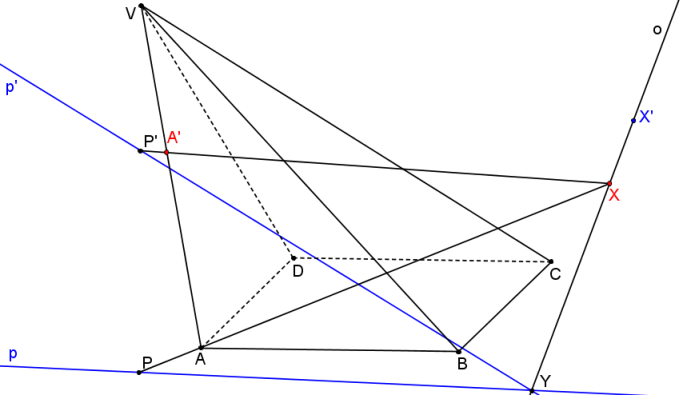

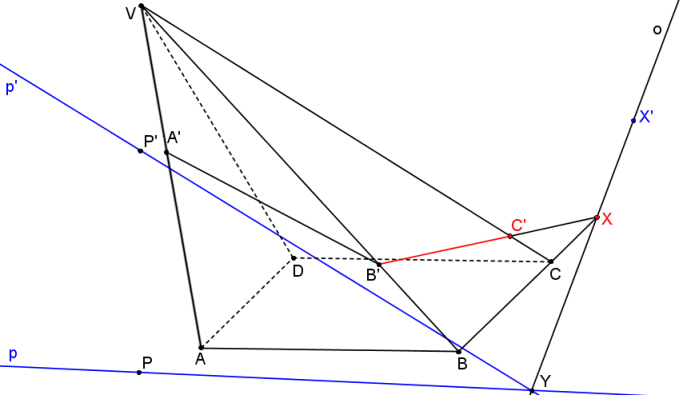
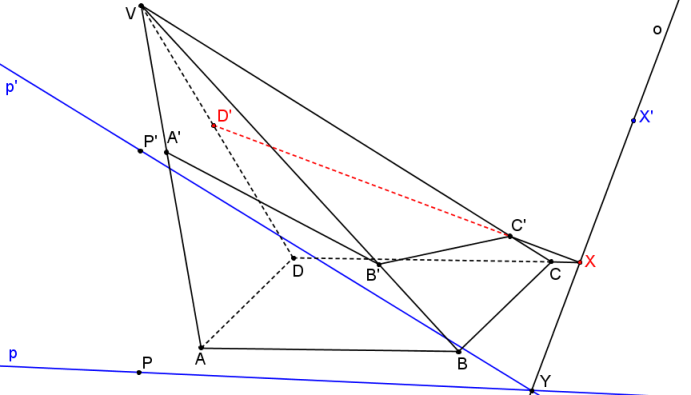
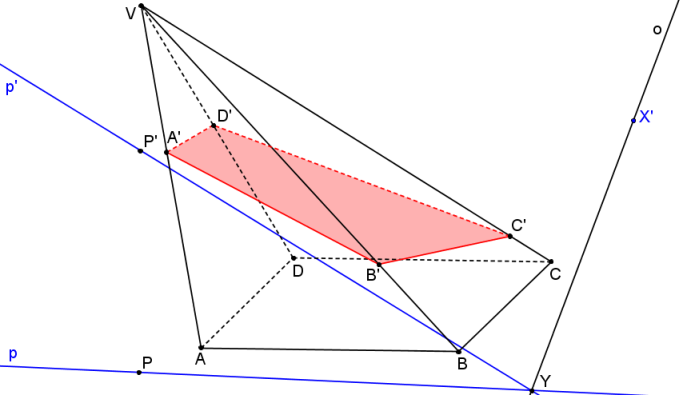
Řezem je čtyřúhelník A´B´C´D´.
V jiných zobrazovacích metodách je většinou rovina řezu dána svými stopami. Osou kolineace je průsečnice roviny řezu a roviny podstavy, střed kolineace S je vrchol jehlanu V. Bohužel není dána dvojice odpovídajících si bodů. Musíme proto najít jeden bod řezu pomocí jiných konstrukcí. Konstrukce se liší podle jednotlivých promítání, myšlenka konstrukce je však stále stejná. Bod A´ je průsečík hrany jehlanu AV s rovinou řezu.
Další příklady na vypracování s výsledky:
- Volné rovnoběžné promítání: Zadání, Řešení
- Mongeovo promítání: Zadání, Řešení
- Kosoúhlé promítání: Zadání, Řešení
- Pravoúhlá axonometrie: Zadání, Řešení
Tyto úlohy mají více řešení. Uvádíme pouze to řešení, které přímo využívá středovou kolineaci.