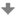\begin{align} \end{align}

Řez kužele

V kapitole budeme pracovat s tělesy, která jsou zobrazena ve volném rovnoběžném promítání

Kužel, kuželový prostor a kuželová plocha

Než začneme pracovat s kuželi, připomeňme definici kuželové plochy a kuželového prostrou. Množina všech přímek procházejících bodem V a protínajících kružnici (kruh) k, která leží v rovině φ neprocházející bodem V, se nazývá kuželová plocha (kuželový prostor) [10] (str. 92). Bod V se nazývá vrchol.

Kužel získáme z kuželového prostoru tak, že jej omezíme dvěma rovinami. Jednou rovinou je zpravidla rovina φ a kružnici k pak nazýváme podstavou kužele. Druhou rovinou je rovina φ´ (φ´||φ) procházející vrcholem V. Vzdálenost rovin φ, φ´ se nazývá výška kužele. Spojnice středu podstavy S s vrcholem V se nazývá osa. Je-li osa kolmá k rovině podstavy, pak se kužel nazývá rotační, jinak je kosý. V textu budeme pracovat s rotačními i kosými kuželi.

Pozn: Kuželová plocha může být obecně množina všech přímek procházející bodem V, které protínají křivku k ležící v rovině φ neprocházející bodem V.

Kužel, kuželová plocha, kolmý a kosý kužel.

Řez kužele

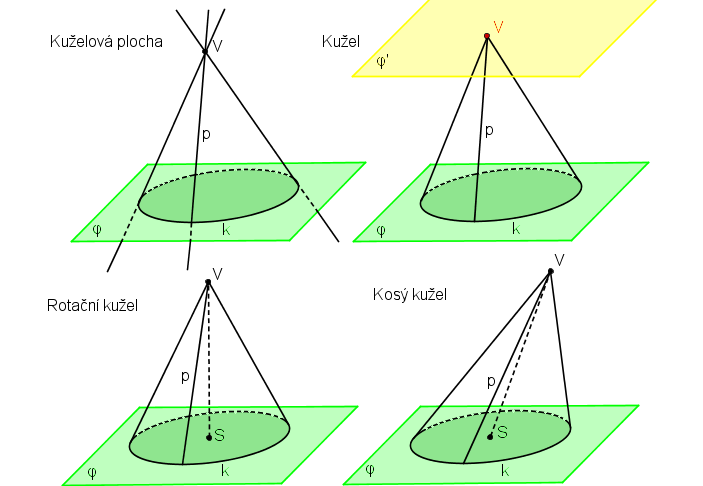
Nejprve se podívejme, jak můžeme volit rovinu řezu α. Speciálním případem je, když rovina α prochází vrcholem kuželu. Této rovině říkáme vrcholová rovina. Pokud průsečnice vrcholové roviny a roviny podstavy φ protíná podstavnou kružnici ve dvou bodech, pak je řezem trojúhelník procházející vrcholem V. (Pokud bychom uvažovali tento řez kuželovou plochou, pak jsou řezem různoběžné přímky procházející vrcholem V.) Pokud tato průsečnice protíná podstavu pouze v jednom bodě (průsečnice je tečnou kružnice), pak je řezem jedna površka. Pokud průsečnice neprotíná podstavnou kružnici, pak je řezem pouze jeden bod - vrchol V. Dalším speciálním případem je, pokud je rovina α rovnoběžná s rovinou podstavy φ. Pak je řezem kružnice. U těchto typů řezů nevyužíváme středovou kolineaci.

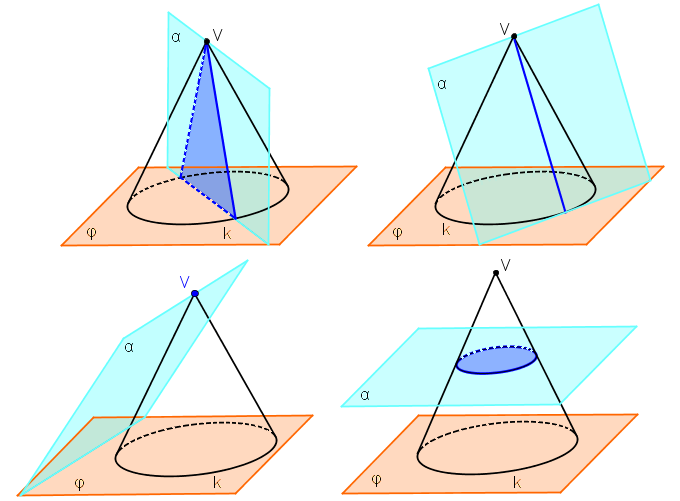
Různe řezy kužele.

Stejně jako u řezu jehlanu, tak i u řezu kužele je mezi rovinou podstavy a rovinou řezu vztah středové kolineace. Osou kolineace je jejich průsečnice, středem kolineace je vrchol kužele V. Párem odpovídajících si bodů je nejčastěji střed podstavné kružnice S a průsečík osy kužele SV s rovinou řezu, ozn. S´. Obrazem kružnice ve středové kolineaci může být elipsa, parabola či hyperbola. Viz klasifikaci. Jsou dva způsoby jak rozlišit, jakou kuželosečkou je řez:

  • Najdeme úběžnici středové kolineace (V, o, S, S´). Podle počtu průsečíků podstavné kružnice s úběžnicí určíme, jakou kuželosečku řez tvoří. Viz klasifikaci.
  • Vrcholem kužele V vedeme vrcholovou rovinu rovnoběžnou s rovinou řezu. Přímka p je průsečnice roviny podstavy a vrcholové roviny. Podle počtu průsečíků podstavné kružnice s přímkou p určíme, jakou kuželosečku řez tvoří. Pokud je přímka p sečnou podstavné kružnice, pak je řezem hyperbola. Pokud je přímka p tečnou podstavné kružnice, pak je řezem parabola. Pokud nemá přímka p s podstavou žádný společný bod, pak je řezem elipsa.
Podstava se ve většině zobrazení promítne jako elipsa. Ve středové kolineaci však platí, stejně jako u kružnice, že obraz elipsy je kuželosečka (elipsa, parabola či hyperbola). Proto můžeme při konstrukcích využít stejných postupů jako v kapitole obrazu kružnice ve středové kolineaci a to i v případě, že je kužel kosý.

Příklad: Je dán rotační kužel, střed podstavy V1, vrchol V. Rovina řezu α je určena průsečnicí o roviny podstavy a roviny α a bodem V´ na ose V1V.


Řešení: Je dán rotační válec. Rovina řezu α je určena přímkou o (průsečnicí roviny podstavy a roviny α) a bodem V´ ležícím na ose V1V.

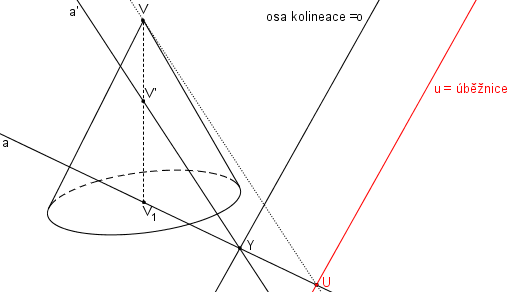
SK (V, o, V1V´). Nejprve najdeme úběžnici u, abychom určili na jakou kuželosečku se podstavná kružnice zobrazí. Postup viz úběžníky a úběžnice. Úběžnice neprotíná podstavnou kružnici v žádném bodě, obrazem je proto elipsa.

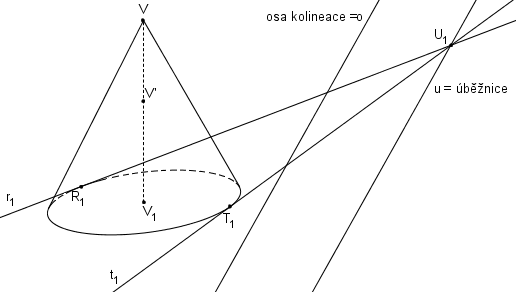
Konstrukce pro obraz kružnice je popsána v kapitole SK Obraz kružnice. Libovolně zvolíme úběžník U1 ze kterého vedeme tečny t1, r1 k elipse.

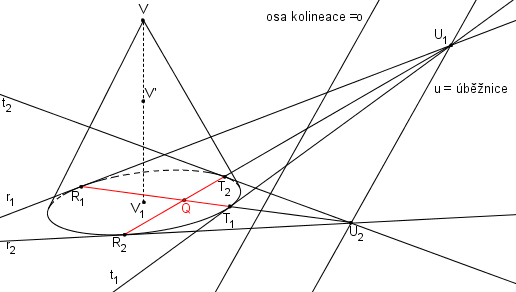
Dotykovými body T1, R1 tečen t1, r1 vedeme přímku, která protíná úběžnici v úběžníku U2, ze kterého vedeme tečny t2, r2 s dotykovými body T1, R1. Úsečky T1R1, T2R2 tvoří tětivy elipsy, které se zobrazí na sdružené průměry elipsy.

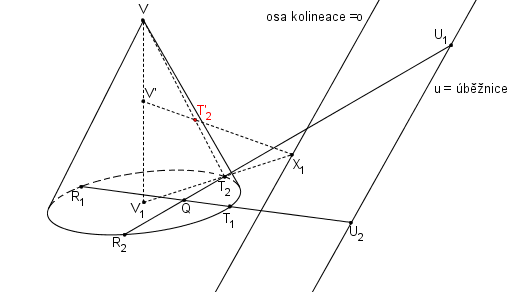
Pomocí SK(V, o, V1V´) najdeme obrazy bodů T1, R1, T2, R2.


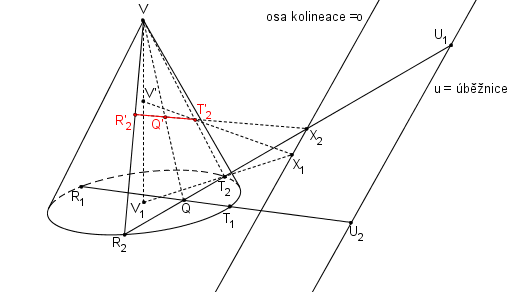
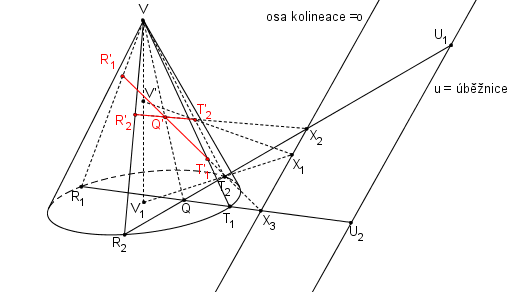
Úsečky T´1R´1, T´2R´2 tvoří sdružené průměry elipsy.

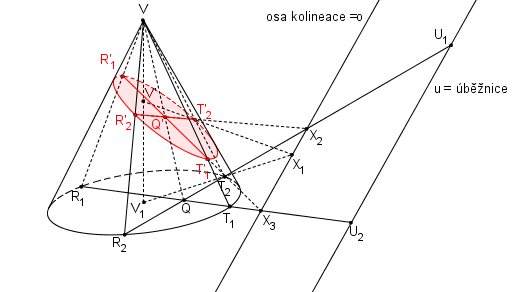
Nyní můžeme vykreslit elipsu.

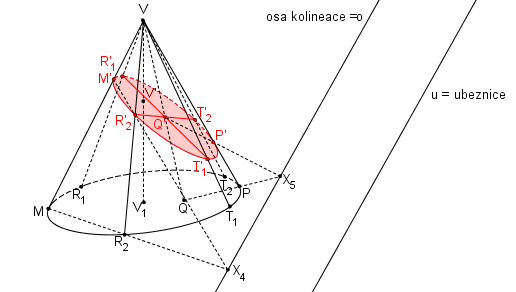
Dotykové body řezu M´,P´ s obrysem kuželu najdeme jako obrazy bodů M, P. Body M, P jsou dotykové body obrysových površek s podstavnou kružnicí. V bodech M´,P´ se mění viditelnost řezu.

Příklad: Je dán rotační kužel, střed podstavy V1, vrchol V. Rovina řezu α je určena průsečnicí o roviny podstavy a roviny α a úběžnicí u.


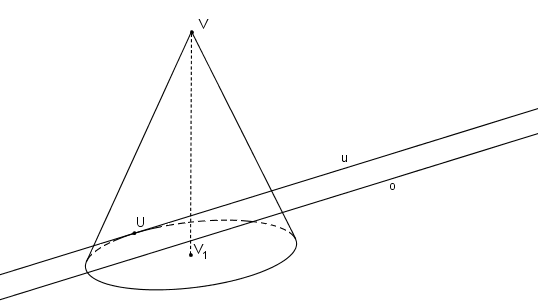
Řešení: Je dán rotační kužel. Rovina řezu α je určena přímkou o (průsečnicí roviny podstavy a roviny α) a úběžnicí u dotýkající se podstavné kružnice v právě jednom bodě U. Protože úběžnice má s podstavnou kružnicí právě jeden společný bod, výsledným řezem je parabola.

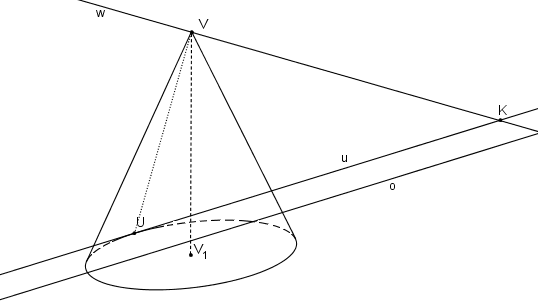
Postupujeme stejně jako v kapitole SK Obraz kružnice. Směr vrcholové tečny určuje přímka w procházející středem kolineace V kolmá k přímce VU. Průsečík w, u označme K.

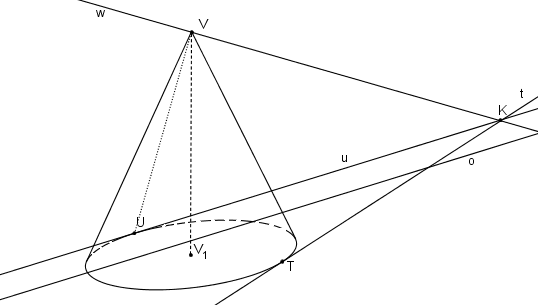
Z bodu K vedeme tečnu t ke podstavné kružnici (různou od úběžnice u). Dotykový bod tečny t s podstavou kružnicí označme T.

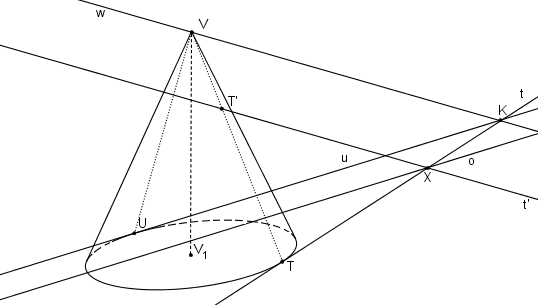
Ve SK(V, o, u) najdeme obraz bodu T.

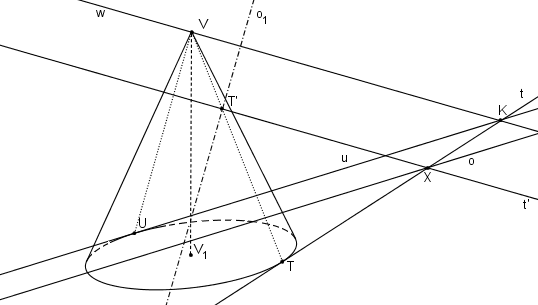
Osa paraboly o1 prochází vrcholem paraboly t´ a je rovnoběžná s přímkou VU (určující směr osy paraboly).

Samodružným bodem R podstavné kružnice vedeme tečnu tR k podstavé kružnici a najdeme její obraz t´R.

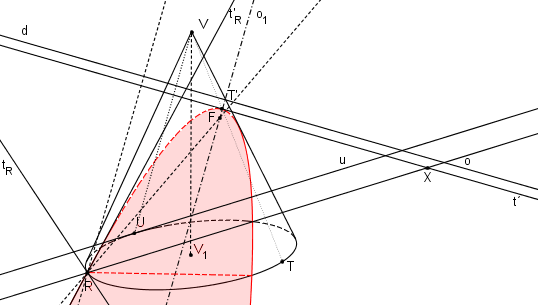
Podle věty: „Tečna půlí vnější úhel průvodičů“, Nalezneme ohnisko paraboly F a vykreslíme parabolu.

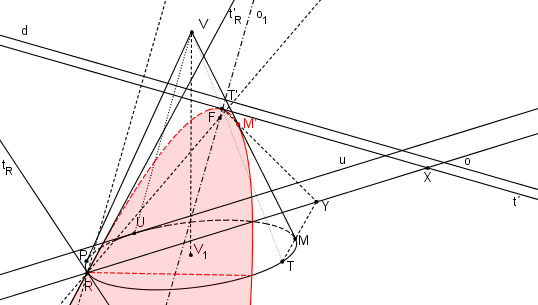
Dotykové body řezu M´,P´ s obrysem kuželu najdeme jako obrazy bodů M, P. Body M, P jsou dotykové body obrysových površek s podstavnou kružnicí. V našem příkladu se do obrázku vešel pouze bod M´. V bodě M´ se mění viditelnost řezu.

Příklad: Je dán rotační kužel, střed podstavy V1, vrchol V. Rovina řezu α je určena průsečnicí o roviny podstavy a roviny α a úběžnicí u.


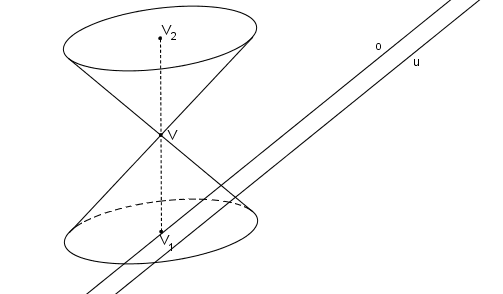
Řešení: Je dán rotační kužel. Rovina řezu α je určena přímkou o (průsečnicí roviny podstavy a roviny α) a úběžnicí u protínající podstavnou kružnici ve dvou bodech. Protože úběžnice má s podstavnou kružnicí právě dva společné body, výsledným řezem je hyperbola. Postupujeme stejně jako v kapitole SK Obraz kružnice.

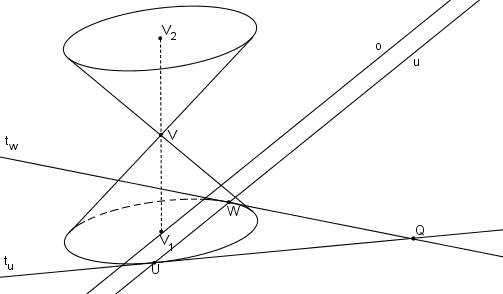
Sestrojíme tečny tu, tw v bodech U, W k podstavné kružnici kružnici. Průsečík tečen je bod Q.

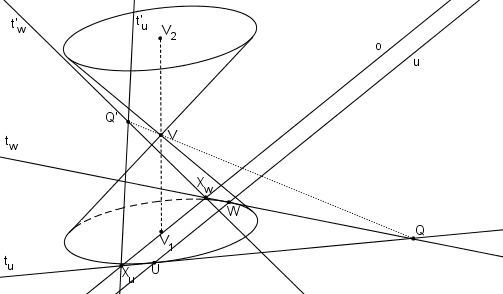
Nalezneme obrazy tečen, t´u ( t´u || UV), t´w ( t´w || WV). Přímky t´u, t´w jsou asymptoty výsledné hyperboly.

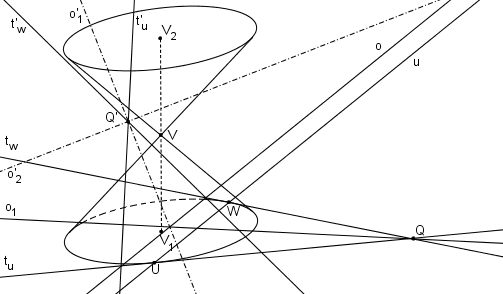
Osy hyperboly o´1, o´2 půlí úhly asymptot. Jako hlavní osu o´1 označíme tu, pro kterou odpovídající přímka o1 protíná podstavou kružnici ve dvou bodech.

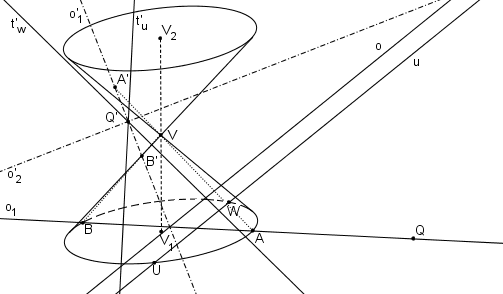
Průsečíky o1 s podstavnou kružnicí označíme A, B a určíme jejich obrazy A´, B´.

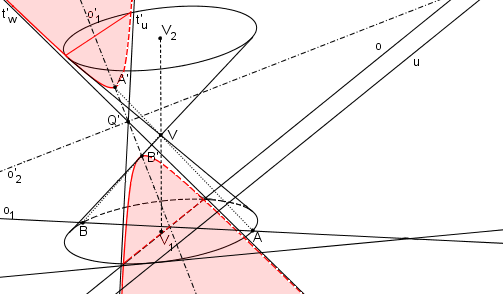
Známe osy hyperboly a její hlavní vrcholy. Můžeme vyrýsovat hyperbolu.

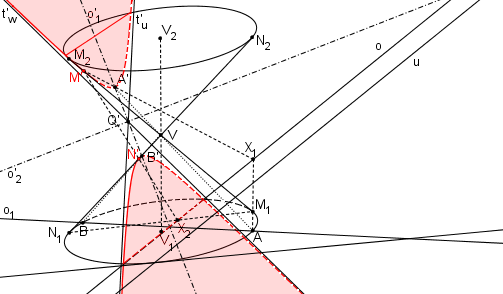
Dotykové body řezu M´,N´ s obrysem kuželu najdeme jako obrazy bodů M1, N1. Body M1, N1 jsou dotykové body obrysových površek s podstavnou kružnicí. V bodech M´,N´ se mění viditelnost řezu.

V jiných zobrazovacích metodách je většinou rovina řezu dána svými stopami. Osou kolineace je průsečnice roviny řezu a roviny podstavy, střed kolineace S je vrchol jehlanu V. Nemusí být vždy zadána dvojice odpovídajících si bodů. Musíme proto najít jeden bod řezu pomocí jiných konstrukcí. Konstrukce se liší podle jednotlivých promítání, myšlenka konstrukce je však stále stejná. Bod S´ je průsečík osy kužele SV s rovinou řezu.

Další příklady na vypracování s výsledky:

Tyto úlohy mají více řešení. Uvádíme pouze to řešení, které přímo využívá středovou kolineaci.