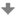Otáčení roviny do průmětny v rovnoběžných promítáních
S osovou afinitou se můžeme setkat při otáčení obecné roviny α do roviny průmětny π, kde rovina α není s rovinou π rovnoběžná. Otočit rovinu znamená najít osu otáčení a otočit její libovolný bod, který neleží na ose otáčení. Osou otáčení je průsečnice roviny α s průmětnou π, tj. stopa pα. Zvolíme libovolný bod A roviny α, který neleží na ose otáčení. Abychom mohli otočit bod A potřebujeme zjistit střed otáčení, poloměr otáčení a rovinu otáčení.
Rovina otáčení ρ bodu A je kolmá k ose otáčení pα.
Střed otáčení SA bodu A je průsečík roviny otáčení ρ s osou otáčení pα.
Poloměr otáčení r bodu A je jeho vzdálenost od středu otáčení SA, r = |AS|.
Otočený bod A (Ao) potom leží na průsečnici roviny otáčení s průmětnou π a na kružnici se středem v bodě SA a poloměrem r.
Zdrojem pro tuto kapitolu je kniha Aloise Urbana Deskriptivní geometrie I [10].
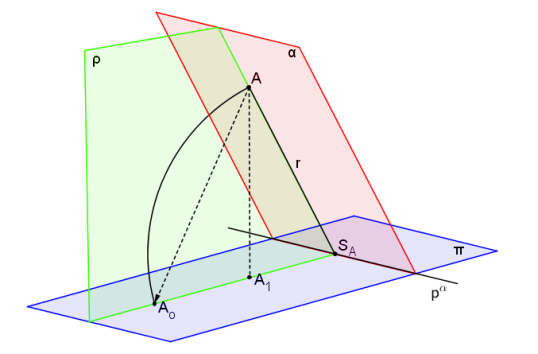
Otáčení roviny do průmětny a osová afinita
Otáčet jednotlivé body roviny α do roviny průmětny π je možné, ale zdlouhavé. K otočení dalších bodů roviny α do roviny průmětny π je výhodnější využít osové afinity mezi rovinami α, π. Osou afinity je průsečnice rovin α, π (tzn. osa otáčení = osa afinity), odpovídající si body jsou bod A a jeho otočená poloha Ao.
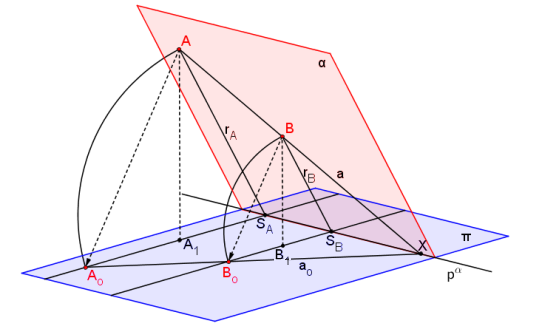
Otáčení roviny do průmětny je prostrová úloha. Proto ji musíme převést do roviny na vztahy mezi body a přímkami. Body a přímky roviny α pravoúhle promítneme do roviny π. Bod A se tak zobrazí do bodu A1 (Pozn. V jednotlivých promítáních pracujeme přímo s bodem A1). Osová afinita v rovině je pak určena stopou roviny α a odpovídajícími si body Ao, A1. Směr Ao, A1 je vždy kolmý k ose afinity, ale nemusí se tak ve všech promítáních zobrazit.
Užití otáčení
Otáčení využijeme například při určování skutečné velikosti rovinného obrazce ležícího v dané rovině α. Pouze v jednom případě vidíme hned skutečnou velikost obrazce a to tehdy, když je rovina α rovnoběžná s průmětnou π. Pokud je rovina α s průmětnou π různoběžná, průmět skutečného obrazce se zkreslí. Například vidíme, že průmětem útvaru je rovnoběžník. Nejsme ale schopni říci, jestli je útvar ve skutečnosti čtverec, obdélník či jen obecný rovnoběžník.
Podobně využijeme otáčení při určování skutečné velikosti řezu. Řez tvoří obecný n-úhelník, který leží v rovině řezu. Postup je stejný jako při určování skutečné velikosti rovinného obrazce. Skutečnou velikost řezu potřebujeme například pro vytvoření modelu.
Obdobnou úlohou je sestrojení útvaru ležícího v rovině. Úkolem je sestrojit například pravidelný n-úhelník ležící v dané rovině α. Protože nevíme, jak se n-úhelník zkreslí, musíme nejprve rovinu α otočit do průmětny. V průmětně vidíme n-úhelník ve skutečné velikosti - můžeme ho tam proto sestrojit. Pomocí osové afinity mezi rovinou α a průmětnou pak otočíme rovinu α zpět do své původní polohy.
Otáčení v různých promítáních
S otáčením se setkáme v různých promítáních, kde je osová afinita určena různými způsoby. Osu afinity určíme lehce, protože osa afinity = osa otáčení = průsečnice rovin α, π. Princip otáčení je všude stejný, ale konstrukce otočeného bodu A (Ao) se v každém promítání trochu liší. K tomu je potřeba více znalostí, které nejsou náplní této práce.
Ukažme si, jak se otáčí například v kótovaném promítání.
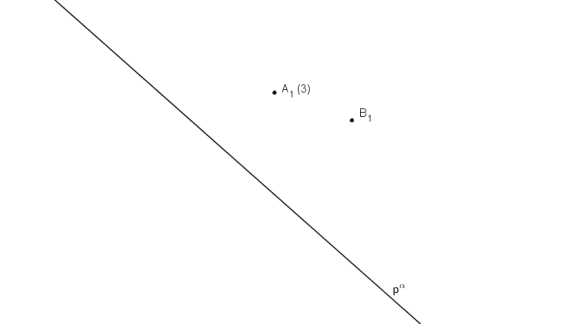
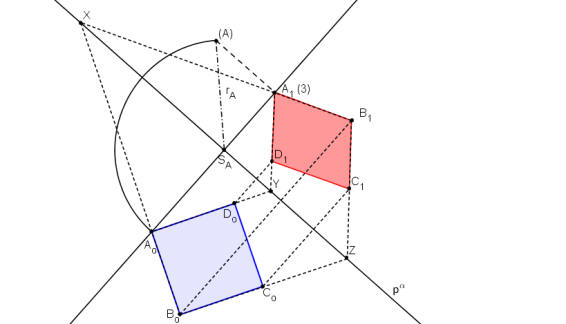
V kótovaném promítání je dána stopa roviny α, ve které leží body A, B. V rovině α sestrojte čtverec ABCD.
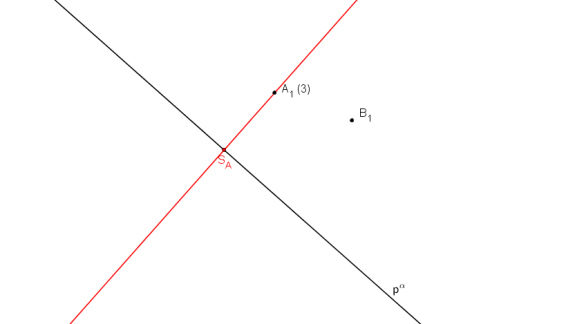
Otočíme bod A. Průsečnice roviny otáčení a průmětny je kolmice ke stopě procházející bodem A1. Průsečíkem této kolmice a stopy roviny α je bod SA.

Pro zjištění skutečné velikost |SA| se bod A1 sklopí.
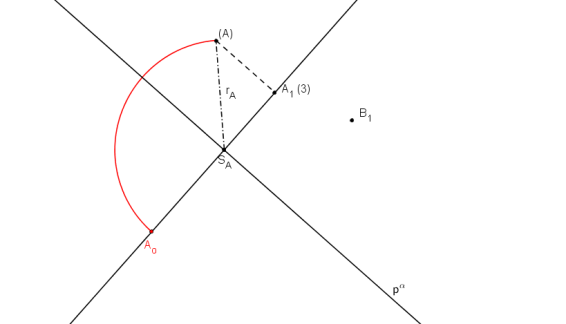
Bod Ao leží na kružnici se středem v bodě SA a poloměrem r.
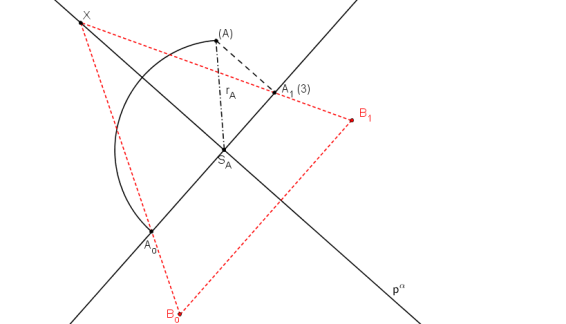
Pomocí osové afity dané pα, A1, Ao najdeme bod Bo

V otočení sestrojíme čtverec AoBoCoDo.
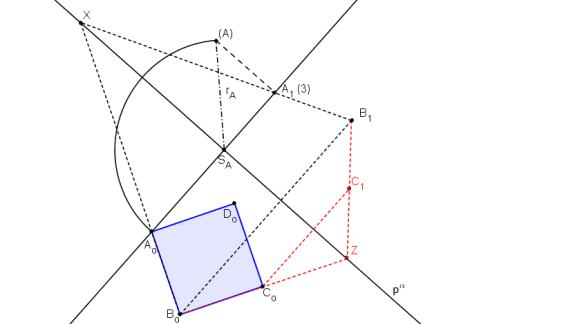
Pomocí osové afinity najděme bod C1.

Pomocí osové afinity najděme bod D1.

A1B1C1D1