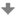Osová afinita v rovině
Osovou afinitu jsme definovali jako vztah v prostoru - vztah mezi dvěma rovinami. Častěji se setkáme s osovou afinitou v rovině, protože rýsujeme v rovině sešitu. Jak převedeme prostorový vztah do roviny? Tento problém vyřešíme stejně jako všechny prostorové vztahy. Zvolíme si směr promítání a všechny prvky rovnoběžně promítneme. Volíme rovnoběžné promítání, protože zachovává rovnoběžnost. Směr promítání volíme tak, aby nebyl rovnoběžný se směrem afinity, jinak by body A, A´ splynuly. Dále nesmí být směr promítání rovnoběžný s žádnou z rovin ρ, ρ´. Zvolíme si rovinu π, do které budeme promítat a směr promítání t. Osu afinity o, odpovídající si body A, A´ promítneme pomocí směru t do roviny π. Pro promítnuté body A, A´ platí opět vztah osové afinity, kde osa afinity o* je průmětem osy o a přímka s*, která určuje směr afinity, je průmětem přímky s, nebo je určen průměty bodů A, A´ (A*, A´*).
Podobně jako v osové afinitě mezi dvěma rovinami se i v osové afinitě v rovině značí osa afinity o, směr afinity s. Vzory bodů se značí A, B, C, ..., obrazy bodů A´, B´, C´,.... Podobně jako body se označují vzory přímek a, b, c,... a obrazy přímek a´, b´, c´....
Takto vypadají již promítnuté prvky osové afinity. S růžovými body lze pohybovat.
Poznámka: V praxi volíme směr t tak, že body A a A* splývají. Zjednodušeně řečeno: Můžeme si představit, že roviny ρ ρ´ zmizí a zůstanou nám pouze „stopy“ přímek a bodů, na které se díváme tak, jako by ležely v rovině papíru a ne jako na prostorové vztahy.
Vlastnosti osové afinity
Jako u všech zobrazení, která známe, je dobré vědět, jaké vlastnosti osová afinita zachovává. Jinak řečeno, co se při zobrazení nemění.
Dělicí poměr
První důležitou vlastností, kterou můžeme při konstrukcích využít je, že osová afinita zachovává dělicí poměr. Pojďme se podívat, co to dělicí poměr je:
Definice
„\(ABC\) jsou tři libovolné vlastní body, ležící na jedné přímce, u nichž platí \(A ≠ B ≠ C\). Dělicí poměr bodu \(C\) vzhledem k bodům \(A, B\) v daném pořadí je reálné číslo \(λ\), jehož absolutní hodnota je rovna podílu velikostí úseček \(\frac{|AC|}{|BC|}\).
- Leží-li bod \(C\) vně úsečky \(AB\), pak je číslo \(λ\) kladné.
-
Leží-li bod \(C\) mezi body \(A, B\), pak je číslo \(λ\) záporné.“
— Piska R, Medek V.: Deskriptivní geometrie I [6]
Dělicí poměr bodů A, B, C značíme (ABC) = λ. Bod A nazýváme prvním základním bodem, bod B druhým základním bodem. Pořadí bodů A, B není libovolné. Pokud mezi sebou vyměníme body A, B, dostaneme vztah: \((ABC)=\frac{1}{(BAC)}\).
Z definice vyplývá, že A ≠ B a B ≠ C. Může však nastat případ, že A = C, potom je λ rovna nule. Známe dělicí poměr pro každý bod přímky až na bod B (druhý základní bod) a nevlastní bod. Dělicí poměr bodu B musíme v definici vynechat. Pokud by platilo B = C, dělili bychom nulou. Můžeme však speciálně pro něj doplnit: „Dělicí poměr bodu B vzhledem k bodům A, B je λ = ∞.“ Toto sdělení můžeme chápat tak, že bod B se nekonečně blíží k bodu C. Velikost úsečky BC je tedy téměř nula a díky tomu hodnota zlomku \(\frac{|AC|}{|BC|}\) roste nade všechny meze, tedy do nekonečna. Podobným způsobem zavedeme i dělicí poměr pro nevlastní bod: „Dělicí poměr nevlastního bodu přímky vzhledem k libovolným dvěma základním bodům A, B této přímky je roven 1.“ Představa by byla taková, že bod C je tak daleko, že vzdálenosti |AC| a |BC| jsou stejné. Nyní máme ke každému bodu přímky přiřazen dělicí poměr - právě jedno číslo λ.
Vlastnost osové afinity, zachovávající dělicí poměr, využijeme hlavně v případě, když zobrazujeme střed úsečky. Díky zachovávání dělicího poměru platí, že (ABS)=(A´B´S´). Speciálně pro střed úsečky platí: (ABS)=(A´B´S´)= -1 (Střed úsečky AB se zobrazí na střed úsečky A´B´).
V osové afinitě se střed úsečky AB zobrazí na střed úsečky A´B´. S růžovým bodem B mohu pohybovat.
Rovnoběžnost
Další vlastností, kterou můžeme využít při konstrukci obrazu v osové afinitě je zachování rovnoběžnosti. Pokud jsou přímky p, q rovnoběžné, pak jsou jejich obrazy p´, q´ také rovnoběžné. Tato vlastnost se využívá, pokud chci najít obraz rovnoběžníku (například čtverce A, B, C, D). Stačí tak najít body A´, B´, C´ a bod D´ doplnit na rovnoběžník, protože víme, že strana A´B´ || C´D´ a A´C´|| B´D´.
V osové afinitě je obrazem čtverce rovnoběžník, protože rovnoběžné přímky se zobrazí opět na rovnoběžky. S růžovými body mohu pohybovat.
Incidence
Vlastnost zachovávání incidence mají všechna zobrazení. Platí, že pokud bod Q leží na přímce q, pak obraz bodu Q (Q´) leží na obrazu přímky q (q´). Nikdy se nemůže stát, že bod, který leží na přímce, se zobrazí do bodu mimo obraz přímky.
Samodružné prvky
Nejprve si řekněme, co jsou samodružné prvky.
Samodružný bod je bod, který se při zobrazení zobrazí sám na sebe. Platí pro něj, že X = X´.
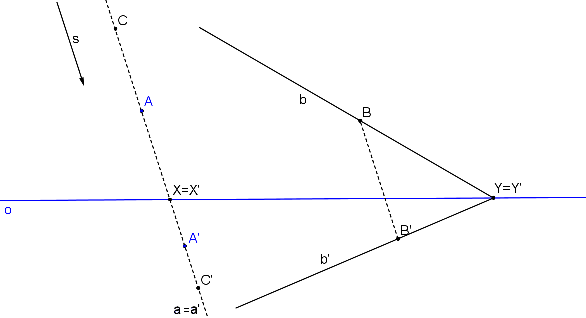
Samodružná přímka je přímka, která se při zobrazení zobrazí sama na sebe. Opět pro ní platí: y = y´. Bod Y, který leží na přímce y se ale zobrazí do jiného bodu (Y´), který opět leží na přímce y, Y ≠ Y´.
Přímka samodružných bodů je přímka, kde každý její bod je samodružný. Pro každý bod na přímce platí X = X´.
V osové afinitě nalezneme samodružnou přímku i přímku samodružných bodů. Na ose afinity leží samodružný bod Y, který náleží přímce b i přímce b´. Toto ale platí pro jakýkoliv bod na ose afinity - osa afinity je přímkou samodružných bodů. Jinak řečeno: Všechny body, které leží na ose afinity jsou samodružné. Samodružné přímky jsou přímky rovnoběžné se směrem afinity. Přímka a || s se zobrazí na a´ tak, že platí a = a´. Pro libovolný bod A, ležící na přímce a (kromě bodu ležího na ose afinity) platí: A ≠ A´.