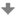Středová kolineace v rovině
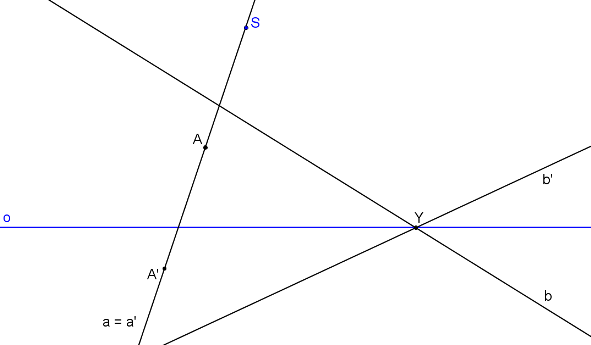
Středovou kolineaci jsme definovali jako vztah v prostoru - mezi dvěma rovinami. Pro řešení úloh je třeba převést vztah z prostoru do roviny. Jak převedeme prostorový vztah do roviny? Tento problém vyřešíme stejně jako všechny prostorové vztahy. Zvolíme si směr promítání a všechny prvky rovnoběžně promítneme. Volíme rovnoběžné promítání, protože zachovává rovnoběžnost. Směr promítání volíme tak, aby nebyl rovnoběžný s žádnou z rovin β, β´ Zvolíme si rovinu π, do které budeme promítat a směr promítání t. Osu kolineace o, střed kolineace S a odpovídající si body A, A´ promítneme pomocí směru t do roviny π. Pro průměty bodů A, A´ platí opět vztah středové kolineace, kde osa kolineace o* je průmětem osy o, střed kolineace S* je průmětem středu S, pár odpovídajících si bodů A*, A´* jsou průměty bodů A, A´.
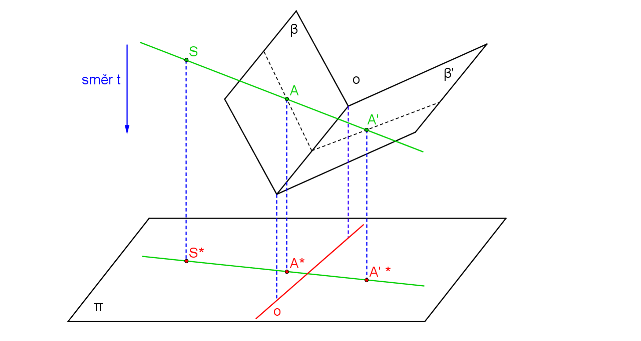
Podobně jako ve středové kolineaci mezi dvěma rovinami se i ve středové kolineaci v rovině značí osa kolineace o, střed kolineace S. Vzory bodů se značí A, B, C, ..., obrazy bodů A´, B´, C´,.... Podobně jako body se označují vzory přímek a, b, c,... a obrazy přímek a´, b´, c´....
Takto vypadají již promítnuté prvky středové kolineace. S růžovými body lze pohybovat.
Vlastnosti středové kolineace
Dvojpoměr
K zavedení dvojpoměru je potřeba dělicí poměr. Dvojpoměr se jako jedna z mála vlastností zachovává ve všech zobrazeních. V zobrazeních, která známe ze střední školy (posunutí, souměrnosti, otáčení) či v osové afinitě platí jiné, jednodušší vlastnosti a proto se v nich s dvojpoměr neuvádí. Na rozdíl od těchto zobrazení, ve středové kolineaci je to jediná vlastnost, která se zachovává.
Definice
Body \(A, B, C, D\) leží na jedné přímce, a platí pro ně \(A ≠ B ≠ C ≠ A\). Dvojpoměr bodů \(A, B, C, D\) je právě jedno číslo \(μ\), pro které platí:
- Je-li \(D ≠ A\) a zároveň \(D ≠ B\), pak \(μ=\frac{(ABC)}{(ABD)}\)
- Je-li \(D = B\), pak \(μ = 0\).
-
Je-li \(D = A\), pak \(μ = ∞\).
— Havlíček K.: Úvod do projektivní geometrie kuželoseček [2]
Dvojpoměr se značí \(μ = (ABCD)\). Může nabývat všech hodnot. Mezi speciální případy patří 0 a ∞, které jsou zahrnuty v definici. Z definice dvojpoměru vidíme, že pokud se C = D, pak je dvojpoměr \(μ\) = 1. K tomu, aby byl dvojpoměr záporný musí být jeden z dělicích poměrů (ABC), (ABD) kladný a druhý záporný. Jeden z bodů C, D tedy musí ležet uvnitř úsečky AB a druhý vně.
Stejně jako u dělicího poměru, také u dvojpoměru záleží na pořadí bodů. Například pro záměnu bodů C, D platí vztah \((ABCD)=\frac{1}{(ABDC)}\). Tento vztah plyne z definice a platí stejně pro záměnu bodů A, B.
Zde jsou základní převody. Je-li (ABCD) = \(μ\), pak
- \((ABDC)=\frac{1}{μ}\)
- \((ACBD)=1 - μ\)
- \((ADBC)=1 - \frac{1}{μ}\)
- \((ACDB)=\frac{1}{1-μ}\)
- \((ADCB)=\frac{μ}{1-μ}\)
Těchto pět možností zahrnuje všechny možné případy záměn, protože platí vztah (ABCD) = (BADC) = (CDAB) = (DCBA) = \(μ\). Slovy vyjádřeno, hodnota dvojpoměru se nezmění, jestliže se mezi sebou zamění poslední dva body a zároveň dva první body. Dvojpoměr se dále nezmění, zamění-li se první dva body s dvěma posledními body.
V případě, že (ABCD) = - 1, říkáme, že body A, B, C, D tvoří harmonickou čtveřici bodů. Body A, B, C, D tvoří harmonickou čtveřici, jestliže dělicí poměry (ABC), (ABD) jsou až na znaménko stejně velké. V literatuře se setkáváme i s jiným označením harmonické čtveřice. Můžeme říkat, že body C, D jsou harmonicky sdruženy vzhledem k bodům A, B. Body C, D oddělují harmonicky body A, B. Bod D je harmonicky sdružen s bodem C vzhledem k bodům A, B, atd.
Rovnoběžnost a dělicí poměr
V osové afinitě je důležitou vlastností zachovávání dělicího poměru. Ve středové kolineaci se dělicí poměr ani rovnoběžnost nezachovává.
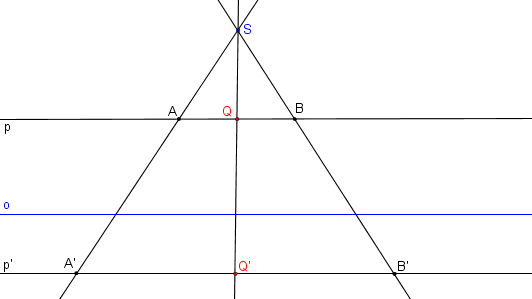
Přímka p je určena body A, B. Bod Q je střed úsečky AB. Bod Q´ se nezobrazí jako střed úsečky A´B´. S růžovým bodem B lze pohybovat.
Applet je vytvořen v programu GeoGebra
Bod Q´ se zobrazí jako střed úsečky A´B´ pouze v případě, že přímka AB (resp. A´B´) je rovnoběžná s osou kolineace o.
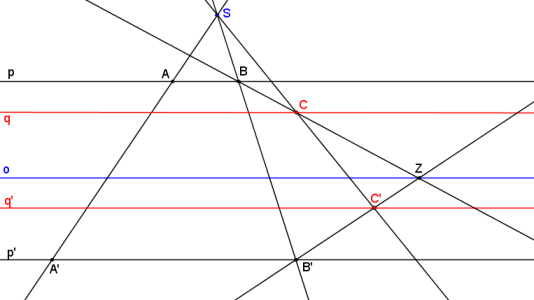
Přímka p je určena body A, B. Přímka q je rovnoběžná s přímkou p a prochází bodem C. Přímky q´, p´ se nezobrazí jako rovnoběžky. S růžovým bodem lze pohybovat.
Applet je vytvořen v programu GeoGebra
Přímky q´, p´ se zobrazí jako rovnoběžky pouze v případě, že přímky p, q jsou rovnoběžné s osou kolineace o.
Incidence
Všechna zobrazení zachovávají incidenci. Platí, že pokud bod Q leží na přímce q, pak obraz Q´ bodu Q leží na obrazu q´ přímky q. Nikdy se nemůže stát, že bod, který leží na přímce, se zobrazí do bodu mimo obraz přímky.
Samodružné prvky
Ve středové kolineaci nalezneme samodružnou přímku, přímku samodružných bodů i samodružný bod. Samodružným bodem ve středové kolineaci je střed kolineace S. Na ose kolineace leží samodružný bod Y, který náleží přímce b i přímce b´. Toto platí pro libovolný bod na ose afinity - osa afinity je přímkou samodružných bodů. Jinak řečeno: Všechny body, které leží na ose afinity jsou samodružné. Samodružné přímky jsou přímky procházející středem kolineace S. Přímka a procházející bodem S se zobrazí na a´ procházející bodem S tak, že platí a = a´. Pro libovolný bod A, ležící na přímce a (kromě samodružného bodu) platí: A ≠ A´.