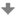Vztah mezi dvěma rovinami
Co si máme pod pojmem středová kolineace představit? Zkusme jednoduchý pokus, který si můžete doma provést. Postavme si na stůl rozsvícenou lampičku a vezměme si tenké desky. Pozorujme stín, který desky vrhají na rovinu stolu. Mezi deskami a jejich stínem je vzájemně jednoznačný vztah, který nazýváme středovou kolineací mezi dvěma rovinami. Podobný vztah můžeme pozorovat také např. večer v ulici osvetlené lampami mezi libovolným plochým předmětem a jeho stínem na chodniku. Vztah mezi člověkem a jeho stínem není přesně vztah středové kolineace, protože lidské tělo neleží v rovině, ale můžeme si ho tak představit.

Ve středové kolineaci platí určité vztahy mezi body a přímkami. Tyto vztahy si přiblížíme na řezu jehlanu rovinou, která neprochází vrcholem V. Rovinné řezy se probírají ve stereometrii na střední škole.
Příklad: Sestrojte řez pravidelného čtyřbokého jehlanu ABCDV rovinou ρ, která je určena body A´, B´, C´; A´ je bodem hrany AV, B´ je bodem hrany BV, C´ je bodem hrany CV.
Krokované řešení: Zadání úlohy

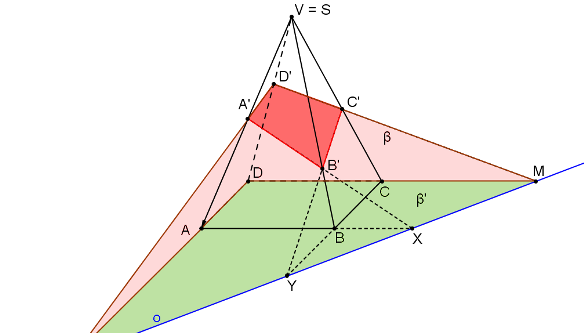
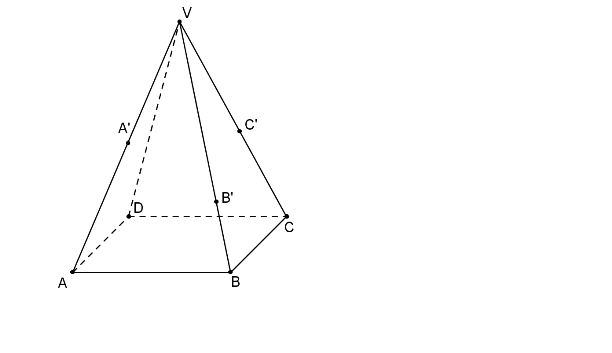
Nejdříve sestrojíme průsečnici o roviny řezu a roviny podstavy: Jeden její bod Y najdeme jako průsečík přímek BC a B´C´.
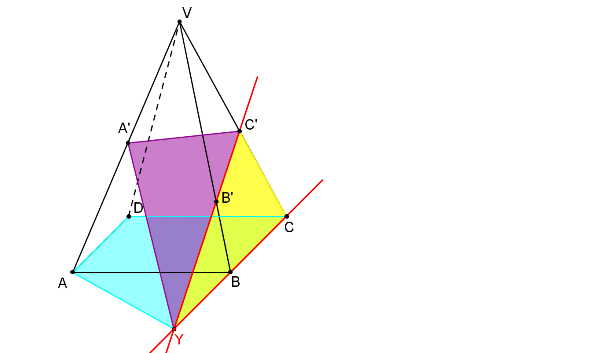
Bod Y je společným bodem trojice rovin ρ, BCV a ABC.
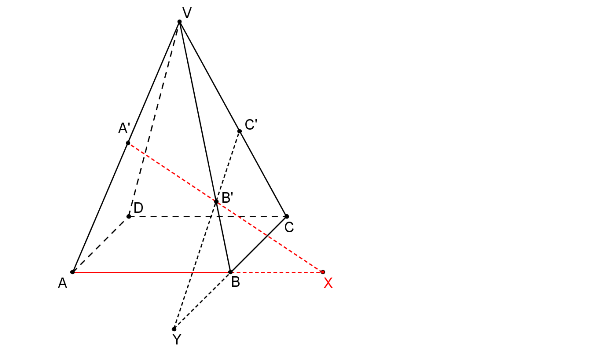
Bod X (průsečík přímek AB a A´B´) je společným bodem trojice rovin ρ, ABC a ABV.
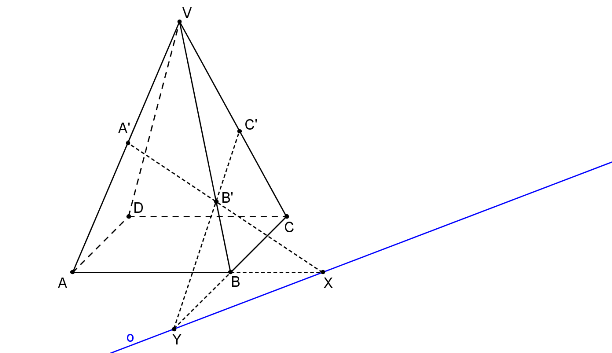
Body X, Y určují přímku o. Přímka o je průsečnice roviny podstavy a roviny řezu.
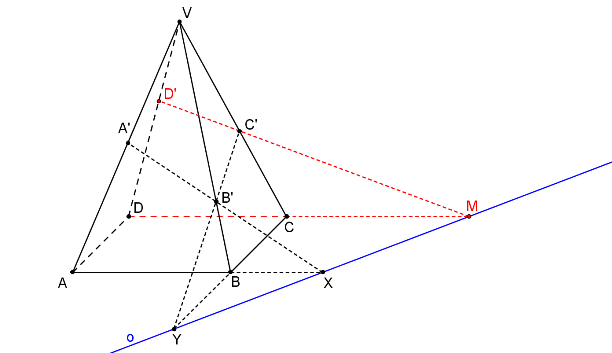
Zbývající bod řezu, D´, sestrojíme pomocí bodu M, který je společným průsečíkem rovin ρ, ABC a CDV. Jinak řečeno: Průsečík přímek CD, C´D´ (bod M) leží na ose o.
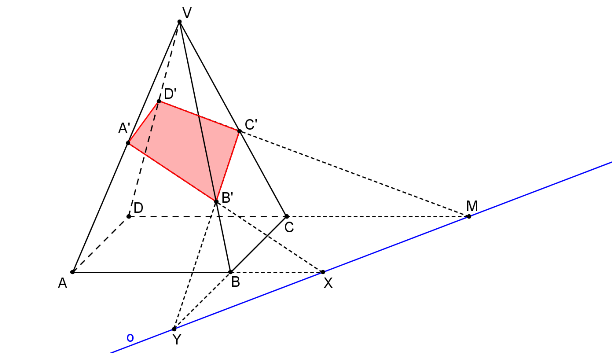
Řezem je čtyřúhelník A´B´C´D´.
Definice
Porovnejme si ukázku s lampičkou a deskami s úlohou „řez jehlanu“. Do vrcholu umístíme lampičku a do roviny řezu umístíme desky tak, aby byly jednou hranou opřeny o stůl. V rovině stolu leží jejich stín. Všimněme si nyní některých vlastností.
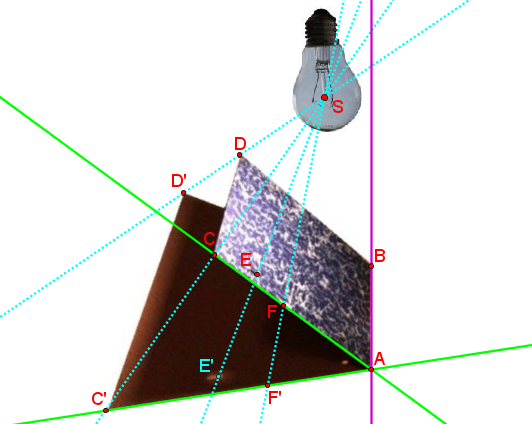
- Roh desek, jeho stín a žárovka leží na jedné přímce. Můžeme si všimnout, že to platí nejen pro každý roh, ale i pro každý bod hrany (pro celý stín). Každá spojnice bodu a jeho stínu prochází zdrojem světla.
- Hrana desek A,B, která leží na stole je totožná se svým stínem. Tato hrana je průsečnice roviny stolu a roviny, ve které desky leží. Hrana neležící na stole, např. A, C, a její stín se protínají na průsečnici roviny stolu a roviny, ve které desky leží.
- Pokud bod leží na libovolné hraně desek, pak jeho stín náleží stínu příslušné hrany.
Příklad lampičky s deskami nám již vlastně celou středovou kolineaci názorně představil. Pojďme se nyní podívat, jak pozorování zobecnit:
Definice
„Uvažujme dvě různoběžné roviny \(β\), \(β´\) s průsečnicí \(o\) a zvolme bod \(S\) tak, že neleží v žádné z rovin. Potom přiřadíme navzájem body a přímky roviny \(β\) bodům a přímkám roviny \(β´\) tak, že platí:
- Spojnice odpovídajících si bodů procházejí bodem \(S\).
- Průsečíky odpovídajících si přímek leží na přímce \(o\).
- Bod na přímce se zobrazí opět do bodu na přímce.
Tuto příbuznost nazveme středovou kolineací mezi dvěma různoběžnými rovinami,
bod \(S\) středem kolineace a přímku \(o\) osou
kolineace.“
— Drábek K., Harant F., Setzer O.: Deskriptivní geometrie I [5]
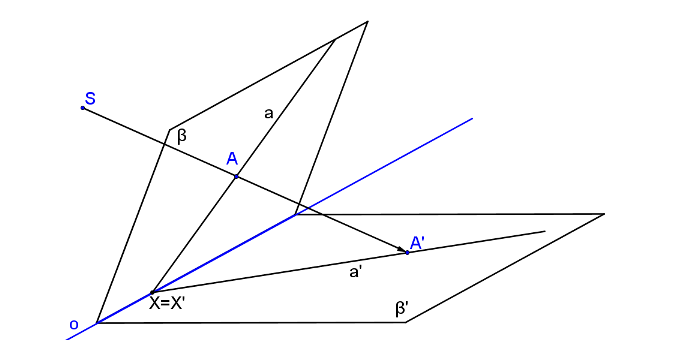
Porovnejme vlastnosti příkladu řez „jehlanu“ se středovou kolineací. Rovina β odpovídá rovině řezu, rovina β´ odpovídá rovině stolu. Střed kolineace S odpovídá vrcholu jehlanu V. Odpovídající si body jsou například body A, A´. Osa o, průsečnice rovin β, β´, je průsečnice roviny podstavy jehlanu a roviny řezu.