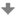Obraz kružnice v osové afinitě
Osová afinita je dána osou o a párem odpovídajících si bodů S, S´. Úkolem je najít obraz kružnice se středem v bodě S a poloměrem r. Pomocí metod analytické geometrie lze snadno dokázat, že obrazem kružnice v osové afinitě je regulární kuželosečka. Regulární kuželosečky můžeme klasifikovat podle počtu nevlastních bodů. Elipsa má všechny body vlastní. Parabola má jeden nevlastní bod (má jednu větev). Hyperbola má dva nevlastní body (dvě větve), které leží ve směru asymptot. V osové afinitě se všechny vlastní body zobrazí opět na vlastní. Kružnice je tvořena pouze vlastními body a protože se žádný bod nezobrazí do nevlastního, obrazem kružnice je pouze elipsa. Existují dva způsoby jak tuto elipsu najít.
Sdružené průměry elipsy
Než se pustíme do obrazu kružnice, připomeňme si pojem sdružené průměry elipsy:
- Dva průměry elipsy se nazývají sdružené, jsou-li tečny v krajních bodech jednoho průměru rovnoběžné s druhým průměrem a naopak.
Přímá konstrukce hlavní a vedlejší poloosy
V osové afinitě mezi dvěma rovinami, která není osovou souměrností, existují právě dva vzájemně kolmé směry, jejichž obrazy jsou v osové afinitě opět vzájemně kolmé směry. Tyto směry určíme takto:
- Je-li osová afinita pravoúhlá, je jeden z nich směr afinity a druhý je určen osou afinity.
- Je-li osová afinita šikmá, zvolíme její libovolnou dvojici odpovídajících si bodů A, A´, sestrojíme kružnici τ procházející body A, A´ a mající střed na ose afinity o a určíme její průsečíky X, Y s touto osou. Hledané směry jsou určeny přímkami AX, AY
— Kraemer E.: Zobrazovací metody [4]
Pro elipsu platí, že jediné dva sdružené průměry, které jsou na sebe kolmé jsou hlavní a vedlejší osy. Hledáme proto takové kolmé průměry kružnice, které se zobrazí opět na kolmé. Díky předchozí větě je nalezneme jednoduše.
Je dána šikmá OA (o, SS´). Dále je v osové afinitě dána kružnice k se středem v bodě S. Hledáme obraz této kružnice v zadané OA. Kružnice τ prochází body S, S´. Proto leží střed kružnice τ (bod T) na ose úsečky SS´. T leží zároveň na ose afinity o (dle předchozí věty). Průsečíky kružnice τ (T, |TS|) s osou o jsou body X, Y. Přímky XS, YS jsou na sebe kolmé. Také jejich obrazy (přímky XS´, YS´) jsou na sebe kolmé. Velikost hlavní a vedlejší poloosy určíme jednoduše. Průsečíky přímek SX, SY s kružnicí k, označme A, B, C, D. Na přímkách S´X, S´Y leží body A´, B´, C´, D´. Tyto body tvoří vrcholy elipsy.
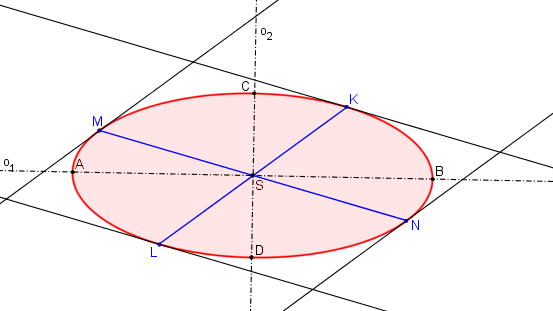
Krokované řešení: OA je dána o, S, S´. Najděte obraz kružnice k.
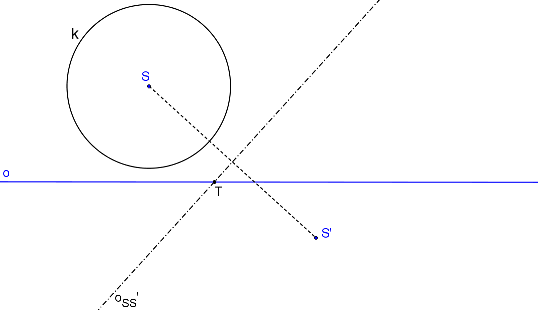
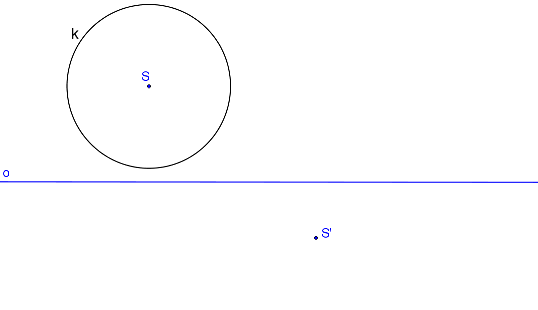
Průsečík osy afinity a osy oSS´ označme T.
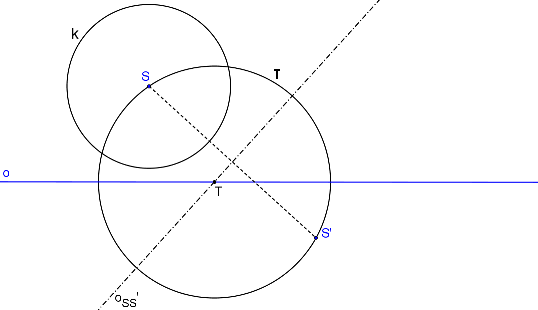
τ (T, |TS|).
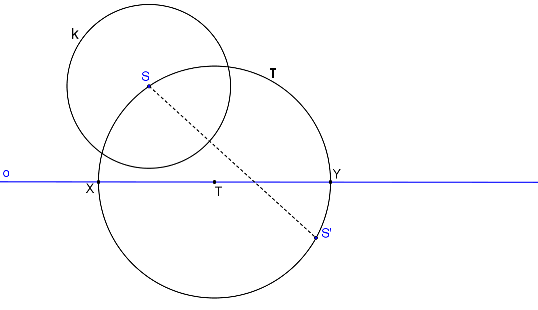
Body X, Y jsou průsečíky kružnice τ s osou o.
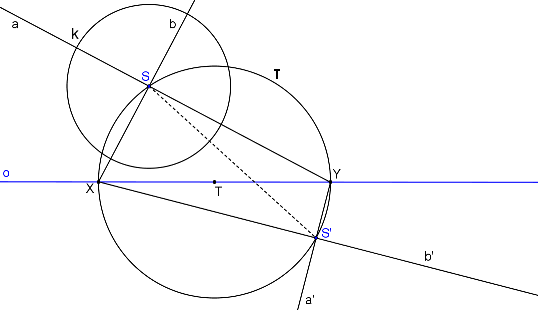
Přímky SX, SY jsou vzájemně kolmé přímky, které se zobrazí na vzájemně kolmé přímky S´X, S´Y.
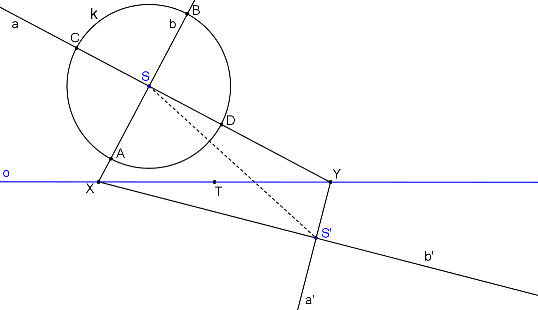
Body A, B, C, D jsou průsečíky zadané kružnice s přímkami SX, SY.
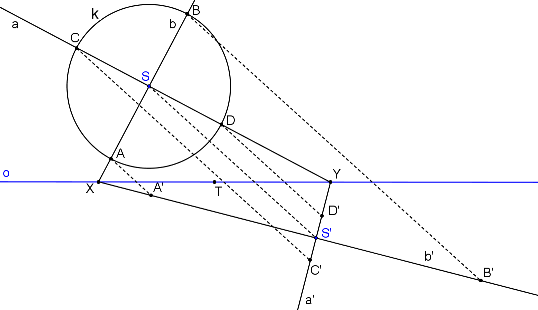
Obrazy bodů A, B, C, D (A´, B´, C´, D´) leží na přímkách S´X, S´Y.
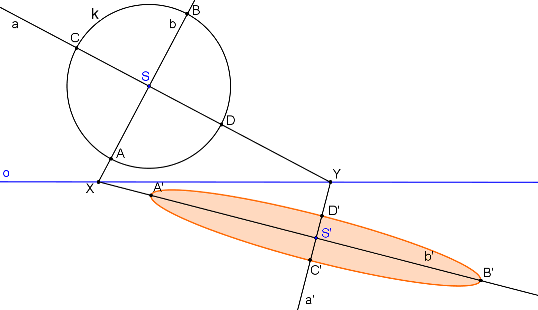
Známe hlavní a vedlejší vrcholy - sestrojíme elipsu.
Nepřímo pomocí Rytzovy konstrukce
V kružnici zvolíme dva libovolné na sebe kolmé průměry (KL),(MN) a najdeme jejich obrazy (K´L´, M´N´). Osová afinita nezachovává úhly, takže tímto postupem nejsou určeny hlavní a vedlejší osy. Zachovává se ale rovnoběžnost a dělicí poměr. Proto tvoří úsečky K´L´ a M´N´ sdružené průměry elipsy. Známe-li dva sdružené průměry elipsy, využijeme k nalezení hlavní a vedlejší osy Rytzovu konstukci.
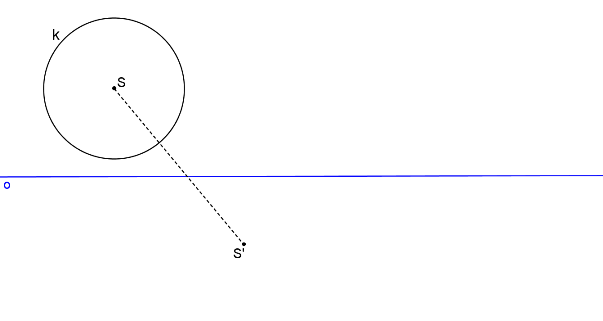
Krokované řešení: Osová afinita je dána osou o a párem odpovídajících si bodů S, S´. Najděte obraz kružnice k.
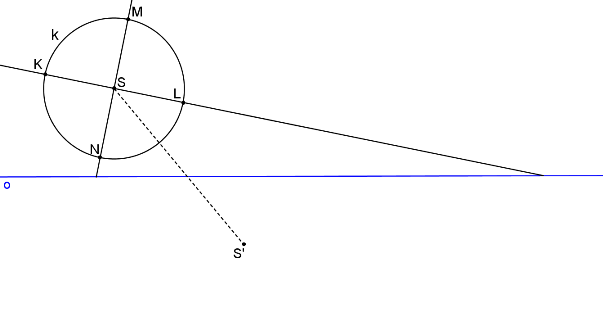
Libovolně zvolíme dva na sebe kolmé průměry kružnice KL, MN.
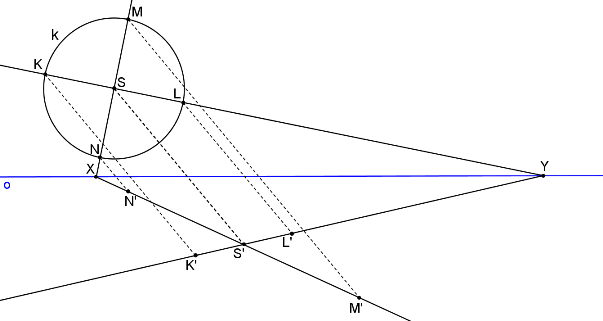
Nalezneme obrazy kolmých průměrů, které tvoří sdružené průměry elipsy - K´L´, M´N´
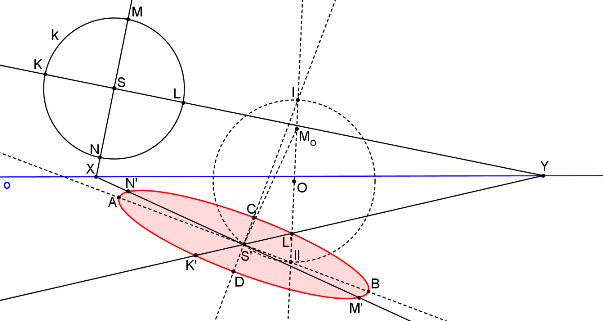
Pomocí Rytzovy konstrukce sestrojíme hlavní a vedlejší osu elipsy.
Rytzova konstrukce
Rytzovou konstrukcí lze dohledat hlavní a vedlejší osy elipsy, pokud známe dvojici sdružených průměrů elipsy. Nechť jsou dány sdružené průměry KL, MN. Jejich průsečík S je středem hledané elipsy, protože střed se zobrazí opět na střed (viz vlastnosti osové afinity). Zvolíme jeden z koncových bodů jednoho průměru, např. bod L. Bod L otočíme o 90° kolem středu S do bodu Lo. Bodem Lo a koncovým bodem druhého průměru, např. N, je určena přímka p. Střed úsečky LoN označme O. Kružnice k má střed v bodě O a poloměr |OS|. Kružnice k protíná přímku p ve dvou bodech, I a II. Osy elipsy o1, resp. o2 jsou určeny body S, II, resp. S, I. Hlavní osa elipsy o1 leží vždy v ostrém úhlu sdružených průměrů. Pro velikosti hlavní a vedlejší poloosy platí: |LoI|=b, |LoII|=a. Hlavní vrcholy elipsy (A, B) leží na ose o1 ve vzdálenosti a od středu S. Vedlejší vrcholy elipsy (C, D) leží na ose o2 ve vzdálenosti b od středu S.
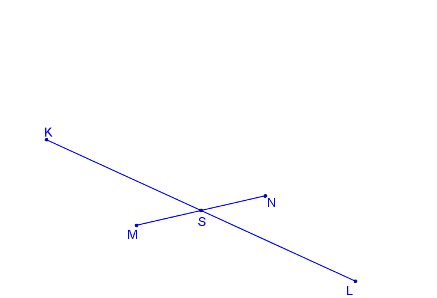
Krokované řešení: Jsou dány sdružené průměry elipsy KL, MN.
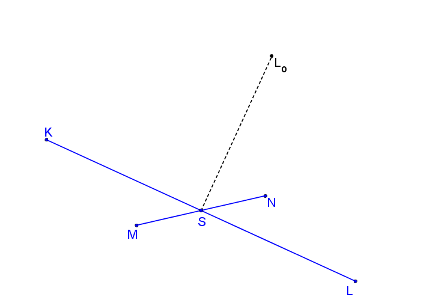
Bod L otočíme o 90° kolem bodu S, ozn. Lo.
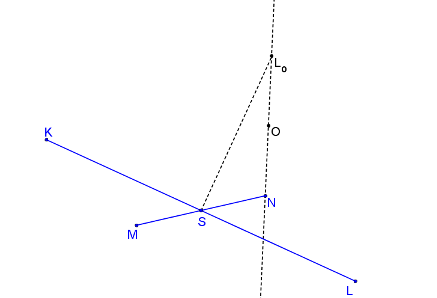
Sestrojíme úsečku LoN, její střed označme O.
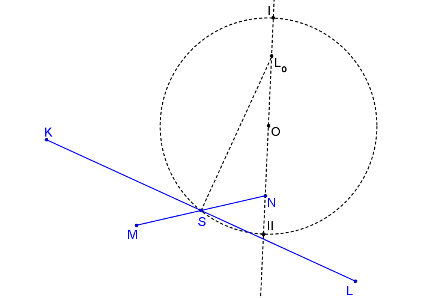
Sestrojíme kružnici se středem v bodě O a poloměrem |OS|. Průsečíky této kružnice s přímkou LoN označme I, II. Bod II leží vždy v ostrém úhlu sdružených průměrů.
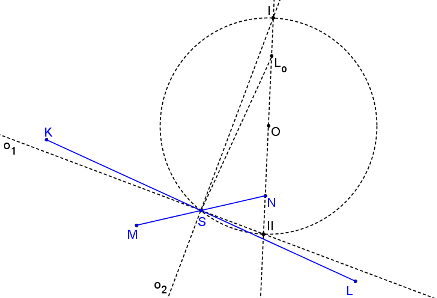
Osy elipsy o1 (resp. o2) jsou určeny body SII (resp. SI).

|LoI|=b.
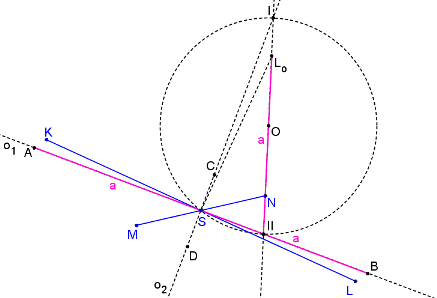
|LoII|=a.
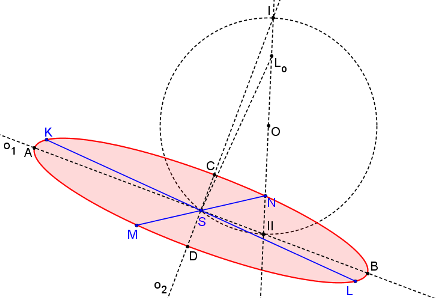
Známe hlavní a vedlejší vrcholy - sestrojíme elipsu.
Příklady na využití osové afinity při konstrukcích elipsy či řešení poloh přímky s elipsou nalezete v kapitole Konstrukce elipsy nebo Přímka a elipsa