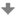Obraz kružnice ve středové kolineaci
Klasifikace
Obrazem kružnice ve středové kolineaci je regulární kuželosečka a to elipsa, parabola nebo hyperbola. Pomocí metod analytické geometrie to lze snadno dokázat. Proč může být obrazem kružnice i parabola a hyperbola, když v osové afinitě může být obrazem kružnice pouze elipsa? Z kapitoly o úběžnicích víme, že ve středové kolineaci existují vlastní body, které se zobrazí na nevlastní body, tzv. úběžníky. Tato vlastnost je důležitá, protože regulární kuželosečky můžeme klasifikovat podle toho, kolik mají nevlastních bodů. Elipsa má všechny body vlastní. Parabola má jeden nevlastní bod (má jednu větev). Hyperbola má dva nevlastní body (dvě větve), které leží ve směru asymptot.
Ke konstrukci kuželosečky nejprve určíme na jakou kuželosečku se kružnice zobrazí. Z předchozího odstavce víme, že regulární kuželosečky se liší podle počtu nevlastních bodů. Ve středové kolineaci jim říkáme úběžníky a leží na úběžnici. Díky tomu platí, že:
- Nemá-li kružnice s úběžnicí žádný společný bod, pak je obrazem kružnice elipsa. (Nemá žádný bod, který by se zobrazil na nevlastní.)
- Má-li kružnice s úběžnicí právě jeden společný bod, pak je obrazem kružnice parabola. (Má jeden bod, který se zobrazí na nevlastní.)
- Má-li kružnice s úběžnicí dva různé průsečíky, pak je obrazem kružnice hyperbola. (Má dva body, které se zobrazí na nevlastní.)
Elipsa
Sdružené průměry
Elipsu sestrojíme pomocí Rytzovy konstrukce. Na Rytzovu konstrukci jsou potřeba sdružené průměry. Úkol se zdá jednoduchý, ale nesmíme zapomenout, že středová kolineace nezachovává dělicí poměr, takže střed kružnice se nezobrazí na střed elipsy. Také průměr kružnice se ve středové kolineaci nezobrazí na průměr elipsy. Průměr elipsy má tu vlastnost, že tečny v jeho koncových bodech jsou navzájem rovnoběžné. Ve středové kolineaci však nesmíme zapomenout, že přímky, které se zobrazí na rovnoběžky se protínají na úběžnici. Proto tětivu kružnice, která se zobrazí na průměr elipsy, najdeme jako spojnici dotykových bodů tečen vedených z libovolného bodu úběžnice. Na úběžnici si proto libovolně zvolíme úběžník U1, kterým bude procházet tětiva p1. Dále sestrojíme tečny t1, r1 ke kružnici k z úběžníku U1. Dotykovými body T1, R1 je určena druhá tětiva p2. Přímka p2 protíná úběžnici v úběžníku U2. Z bodu U2 vedeme tečny t2, r2 ke kružnici k. Dotykovými body tečen t2, r2 (T2, R2) je určena tětiva p1. Tětivy p1, p2 jsou díky konstrukci takové tětivy kružnice, které se zobrazí na sdružené průměry elipsy.
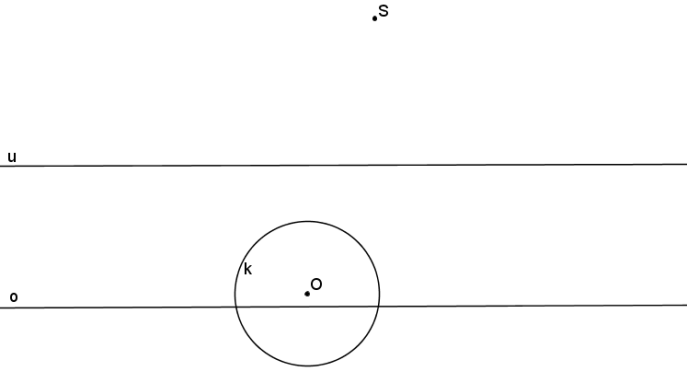
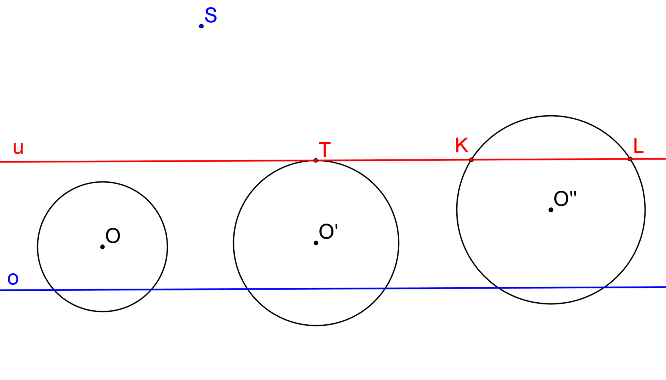
Krokované řešení: SK je dána S, o, u a kružnice k se středem v bodě O tak, aby kružnice s úběžnicí neměla žádný společný bod.
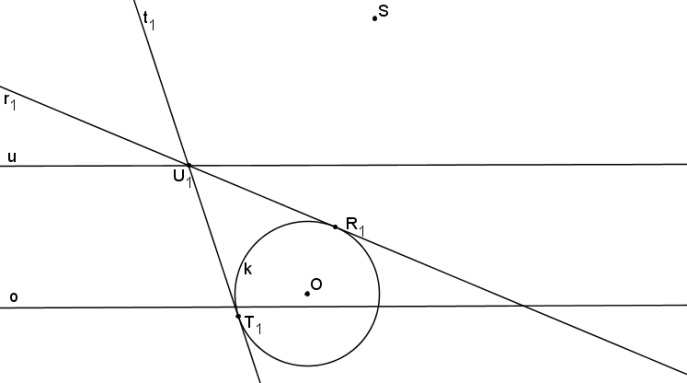
Na úběžnici zvolíme libovolný úběžník U1. Z bodu U1 vedeme tečny t1, r1 ke kružnici k.
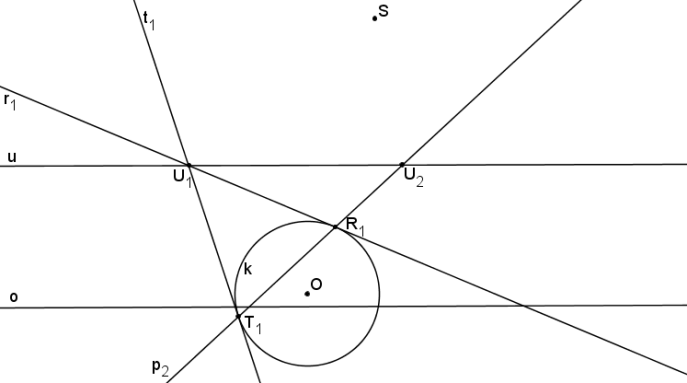
Dotykovými body tečen t1, r1 (T1, R1) je určena tětiva p2. U2 je úběžník přímky p2.
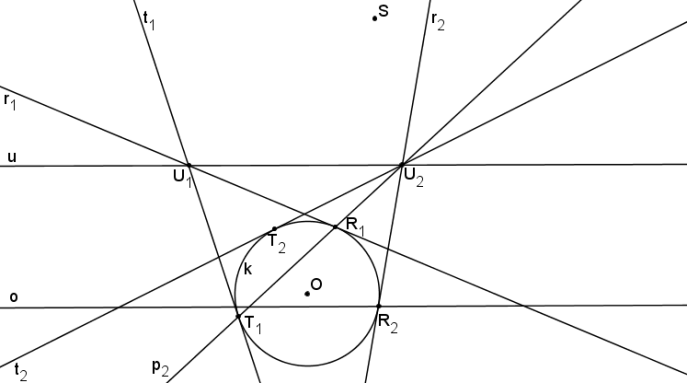
Z bodu U2 vedeme tečny t2, r2 ke kružnici k.
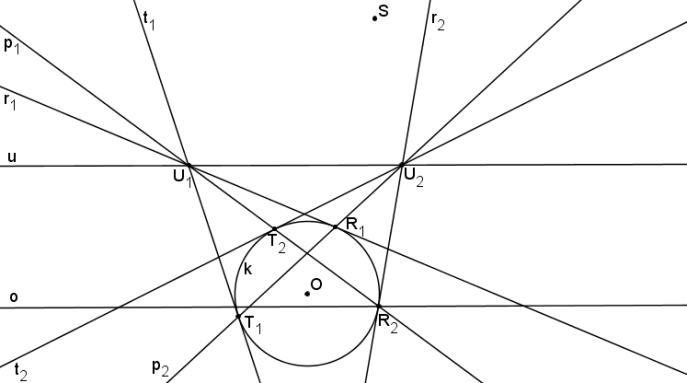
Dotykovými body tečen t2, r2 (T2, R2) je určena tětiva p1. Přímka p1 musí protínat úběžnici v úběžníku U1.

Tětivy T1R1, T2R2 takové jsou takové tětivy kružnice, které se zobrazí na sdružené průměry elipsy. Bod Q se zobrazí na střed elipsy.
Můžete se přesvědčit, že postup nezávisí na volbě úběžníku U1. S růžovým bodem U1 lze pohybovat.
Applet je vytvořen v programu GeoGebra
Konstrukce elipsy
Pro konstrukci elipsy jako obrazu kružnice ve středové kolineaci využijeme sdružené průměry. Z předchozího odstavce víme, jak tyto průměry najít. Můžeme zvolit úběžník U1 libovolně a podle předchozí konstrukce najít úběžník U2. Můžeme však využít trochu jednodušší způsob, který lze aplikovat i v případě, že neznáme přesnou polohu úběžnice. Jediný průměr kružnice, který se zobrazí na průměr elipsy je průměr kolmý k ose kolineace procházející středem kružnice, označme ho p. Tečny v koncových bodech tohoto průměru jsou rovnoběžné s osou kolineace a zobrazí se na přímky, které jsou opět rovnoběžné s osou kolineace. Průsečíky přímky p s kružnicí k jsou body K, L. Na přímce p´ najdeme jejich obrazy, body K´, L´. Tyto body jsou krajními body prvního ze sdružených průměrů. Střed úsečky K´L´ označme Q´. Bod Q´ je středem elipsy e. Bod Q není středem kružnice k, ale je to bod, který se zobrazí na střed elipsy. Tečny v krajních bodech K, L průměru p kružnice jsou rovnoběžné s osou kolineace. Stejně také tečny v odpovídajících bodech K´, L´ elipsy jsou rovnoběžné s osou kolineace. Druhá tětiva proto leží na přímce q rovnoběžné s osou kolineace a procházející bodem Q. Obrazem přímky q je přímka rovnoběžná s osou kolineace procházející bodem Q´. Průsečíky přímky q s kružnicí k jsou body N, M. Na přímce q´ leží body N´, M´, které jsou koncové body druhého ze sdružených průměrů. Nyní máme nalezeny sdružené průměry elipsy K´L´, M´N´ a pomocí Rytzovy konstrukce můžeme dorýsovat elipsu.
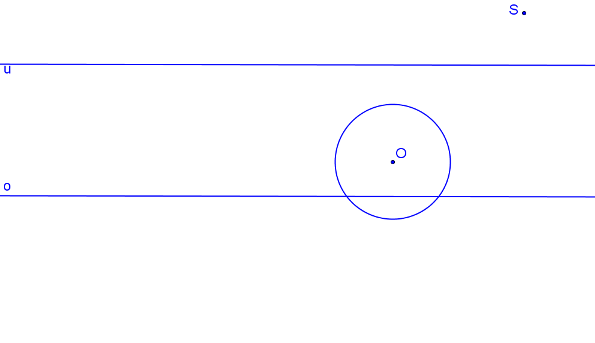
Krokované řešení: Je dán střed kolineace S, osa kolineace o, úběžnice u a kružnice k se středem v bodě O tak, aby kružnice s úběžnicí neměla žádný společný bod.
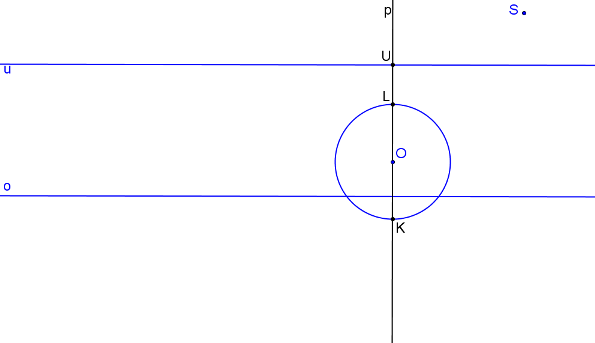
Přímku p je kolmá k ose kolineace. Průsečíky přímky p s kružnicí jsou body K, L. Průsečík přímky p s úběžnicí u je úběžník U.
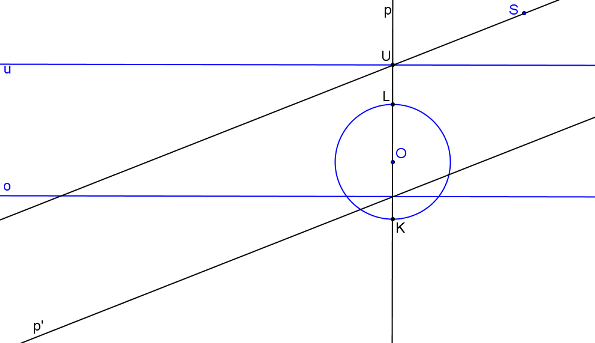
Přímka p´ prochází samodružným bodem přímky p a je rovnoběžná s přímkou SU.
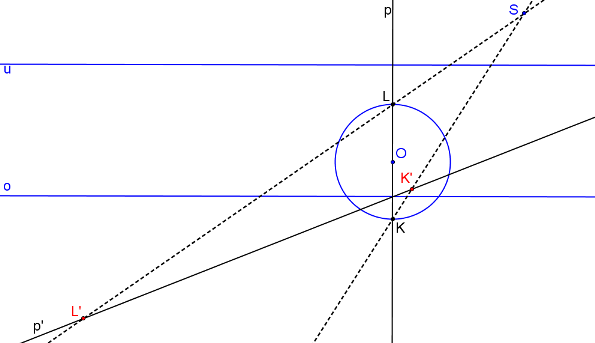
Body K´, L´ leží na přímce p´.
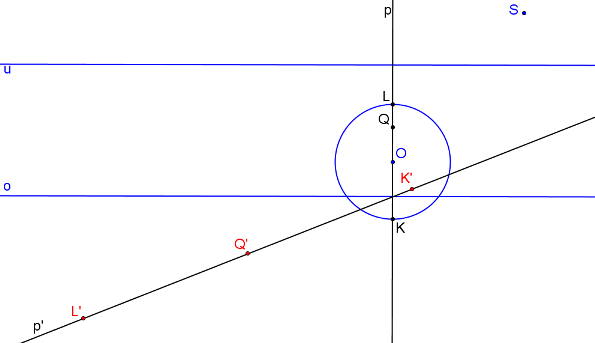
Bod Q´ je střed úsečky K´L´. Bod Q leží na přímce p.
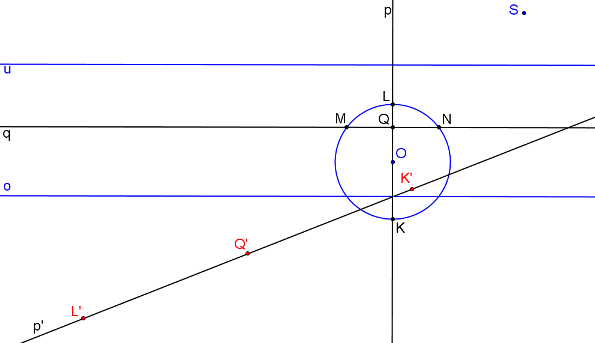
Přímka q je kolmá k přímce p (rovnoběžná s osou kolineace). Body M, N jsou průsečíky přímky q s kružnicí.
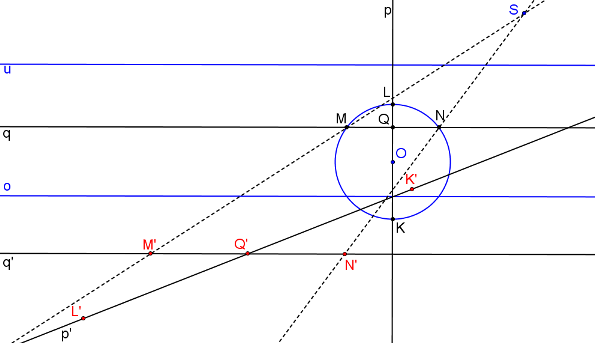
Přímka q´ je rovnoběžná s osou kolineace a prochází bodem Q´. Body M´, N´ leží na přímce q´.
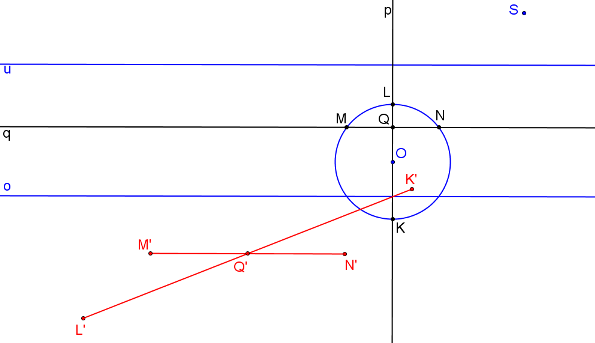
Úsečky K´L´, M´N´ jsou sdružené průměry elipsy.
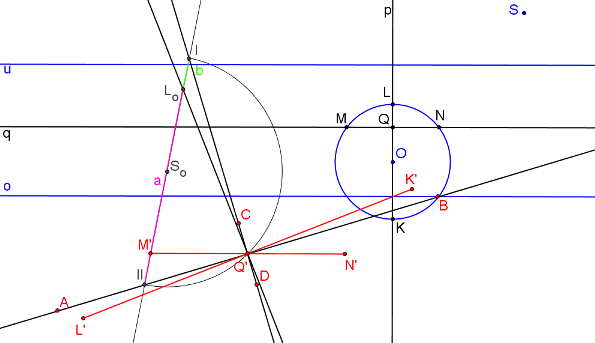
Pomocí Rytzovy konstrukce nalezneme hlavní a vedlejší vrcholy elipsy A, B, C, D.
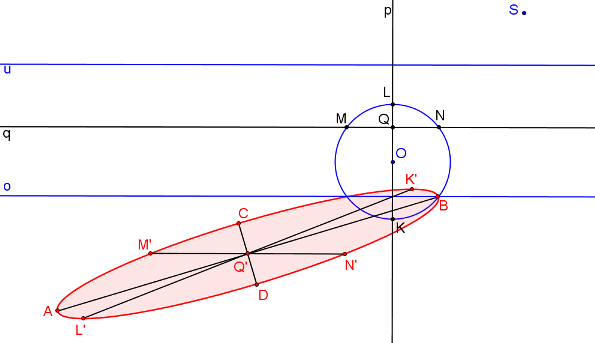
Nyní můžeme sestrojit elipsu.

Pokud kružnice k protíná osu kolineace, pak průsečíky X, Y jsou samodružné body a těmito body prochází i výsledná elipsa.
Parabola
Středová kolineace je dána středem kolineace S, osou kolineace o a úběžnicí u. Dále je dána kružnice k se středem O. Jak již víme, aby byla obrazem kružnice k parabola, musí se kružnice dotýkat úběžnice v jednom bodě, který si označíme U. Nevlastní bod U´∞ je dotykovým bodem paraboly k´ na nevlastní přímce u´∞. Přímka SU je směrem osy sestrojované paraboly k´. Existují dva způsoby, jak parabolu najít:
- Libovolně zvolíme dva body (T, R) na kružnici a sestrojíme jejich tečny (t, r) ke kružnici k. Pokud kružnice protíná osu kolineace je výhodné zvolit body T, R jako průsečíky osy kolineace a kružnice k. Body T, R jsou samodružné, protože leží na ose kolineace. Proto body T, T´ a R, R´ splývají. Dále nalezneme obraz t´, r´ tečen t, r. V našem případě je najdeme velmi jednoduše. Sestrojíme pomocnou přímku p, která je kolmá k ose kolineace a prochází průsečíkem P tečen t, r. Bod P´ leží na přímce p´. Tečny výsledné paraboly t´, r´ jsou určeny body T´P´, R´P´. Nyní známe vše, abychom mohli sestrojit parabolu.
- Přímo nalezneme vrcholovou tečnu v´ s vrcholem V´ hledané paraboly. Přímka SU určuje směr osy paraboly. Vrcholová tečna je kolmá k ose paraboly. Víme proto, že směr vrcholové tečny určuje přímka w procházející středem kolineace S kolmá k přímce SU. Průsečík přímky w s úběžnicí označme K. Jeho obraz K´∞ je nevlastní bod vrcholové tečny v´. Obrazem tečny ke kružnici je tečna k parabole. Proto vedeme z bodu K tečnu v ke kružnici k (různou od úběžnice u). Dotykový bod tečny v s kružnicí k označme V. Obraz v´ tečny v tvoří vrcholovou tečnu. Obraz V´ bodu V tvoří vrchol paraboly. Nyní známe osu paraboly o1 a vrchol paraboly V. Podle předchozí konstrukce najdeme jednu tečnu s bodem dotyku. Parabolu již sestrojíme jednoduše [1] (str. 48).
Víte jak parabolu sestrojit? 
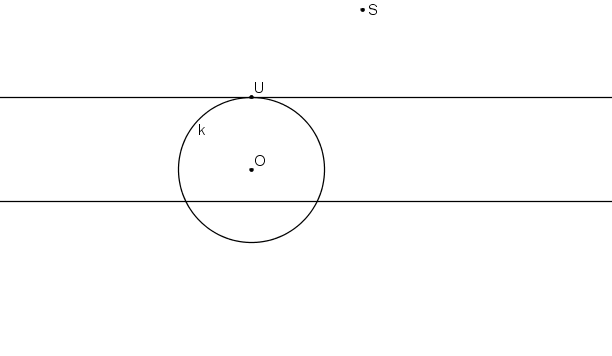
Krokované řešení: Je dán střed kolineace S, osa kolineace o, úběžnice u a kružnice k se středem v bodě O tak, aby kružnice s úběžnicí měla právě jeden společný bod U.
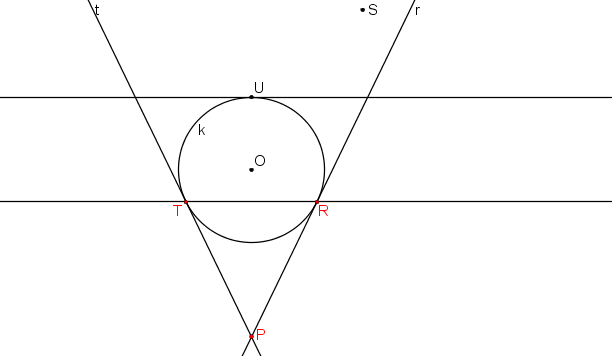
Libovolně zvolíme dva body (T, R) na kružnici a sestrojíme jejich tečny (t, r) ke kružnici k. Průsečík tečen t, r označme P.
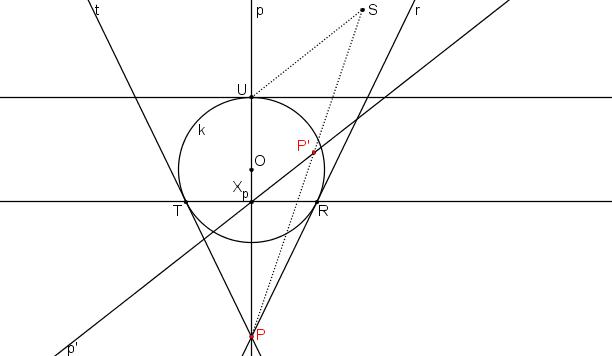
Najdeme obraz P´ bodu P, který leží na obrazu p´ pomocné přímky p. Tečny výsledné paraboly t´, r´ jsou určeny body T´P´, R´P´.
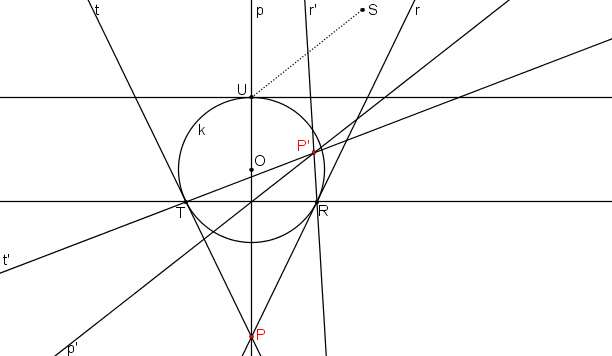
Tečny výsledné paraboly t´, r´ jsou určeny body T´P´, R´P´.
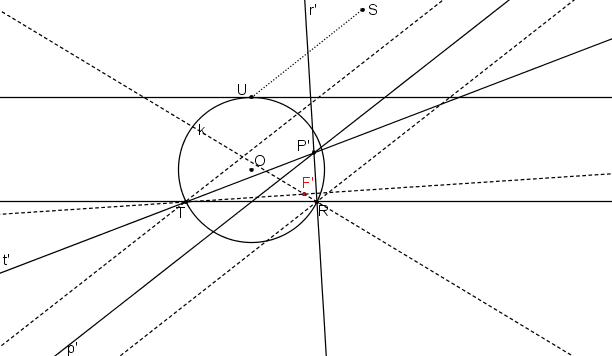
Pomocí věty: "Tečna půlí vnější úhel průvodičů", sestrojíme ohnisko paraboly F´.
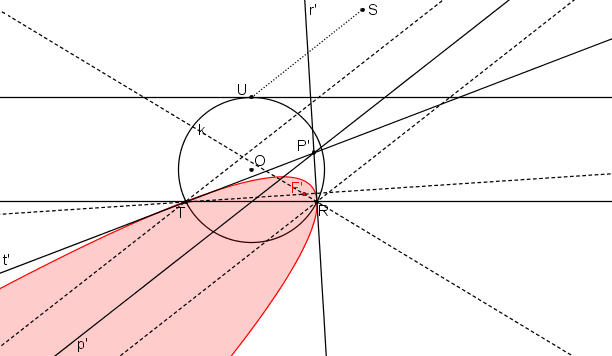
Nyní můžeme parabolu sestrojit.
Je-li bod K přístupný, vyplatí se hledat přímo vrchol paraboly.
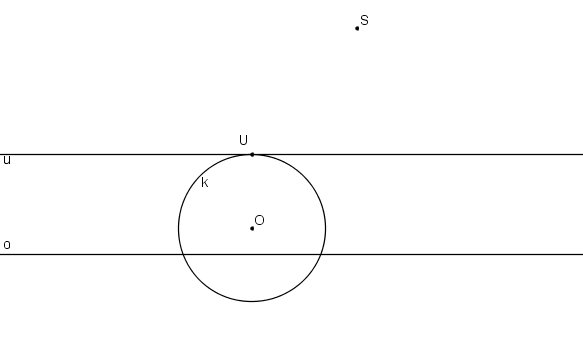
Krokované řešení: Je dán střed kolineace S, osa kolineace o, úběžnice u a kružnice k se středem v bodě O tak, aby kružnice s úběžnicí měla právě jeden společný bod U.
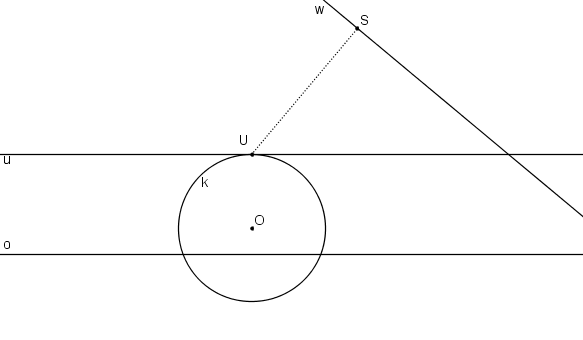
Přímka SU určuje směr osy paraboly. Směr vrcholové tečny určuje přímka w procházející středem kolineace S kolmá k přímce SU.
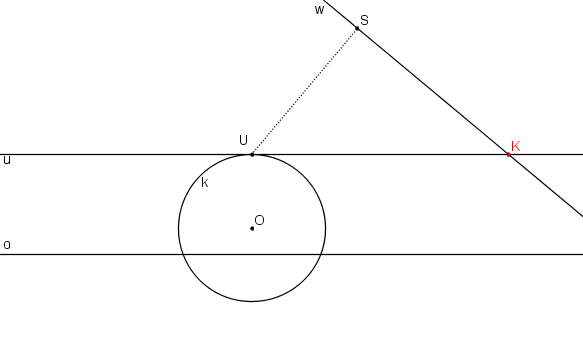
Průsečík přímky w s úběžnicí označme K.

Z bodu K vedeme tečnu v ke kružnici k (různou od úběžnice u). Dotykový bod tečny v s kružnicí k označme V.
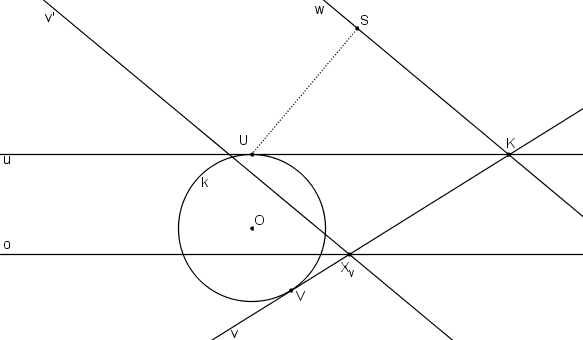
Obraz v´ tečny v prochází samodružným bodem Xv a je rovnoběžný s přímkou w. Přímka v´ tvoří vrcholovou tečnu.

Obraz V´ bodu V leží na vrcholové tečně v´ a tvoří vrchol paraboly.
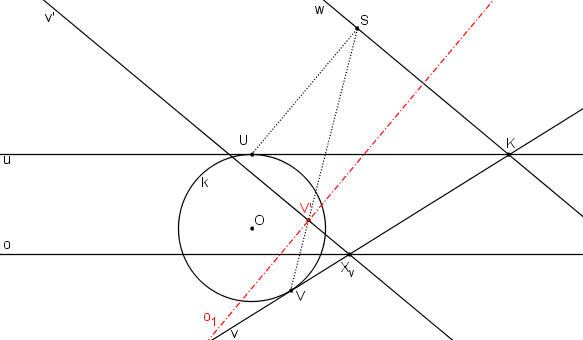
Osa paraboly o1 prochází vrcholem paraboly V a je rovnoběžná s přímkou SU (určující směr osy paraboly).
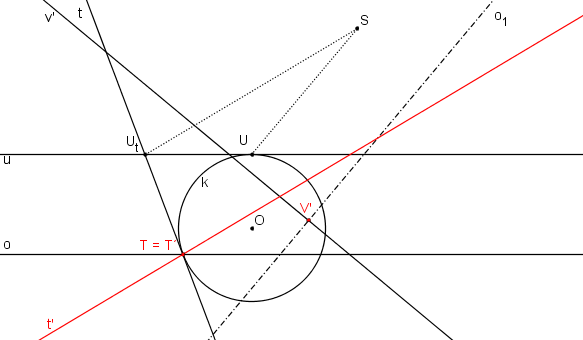
Samodružným bodem T kružnice k vedeme tečnu t ke kružnici k a najdeme její obraz t´.
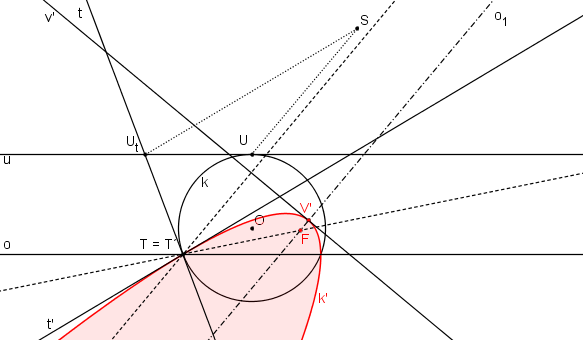
Podle věty: „Tečna půlí vnější úhel průvodičů“, Nalezneme ohnisko paraboly F a vykreslíme parabolu.
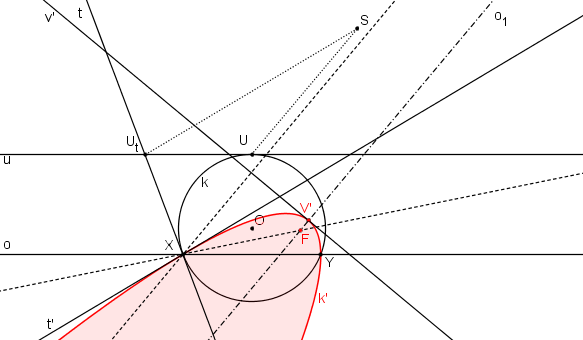
Pokud kružnice k protíná osu kolineace, pak průsečíky X, Y jsou samodružné body a těmito body prochází i výsledná parabola.
Hyperbola
Středová kolineace je dána středem kolineace S, osou kolineace o a úběžnicí u. Dále je dána kružnice k se středem O. Aby obrazem kružnice k byla hyperbola, musí úběžnice protínat kružnici ve dvou bodech. Průsečíky úběžnice u s kružnicí k označme U, V. Bodům U, V odpovídají nevlastní body U´∞, V´∞. Přímky SU, SV určují směry asymptot sestrojované hyperboly. Tečnám au, av v bodech U, V ke kružnici k odpovídají asymptoty a´u, a´v hyperboly k´. Průsečík asymptot a´u, a´v (ozn. Q´) je středem hyperboly. Osy hyperboly půlí úhly asymptot. Jako hlavní osu o´1 označíme tu, pro kterou odpovídající přímka o1 protíná kružnici k ve dvou bodech, označme je A, B. Druhá přímka o2 kružnici k neprotíná. Bodům A, B odpovídají body A´, B´ hyperboly k´ - její hlavní vrcholy. Tím je hyperbola určena [5] (str. 48).
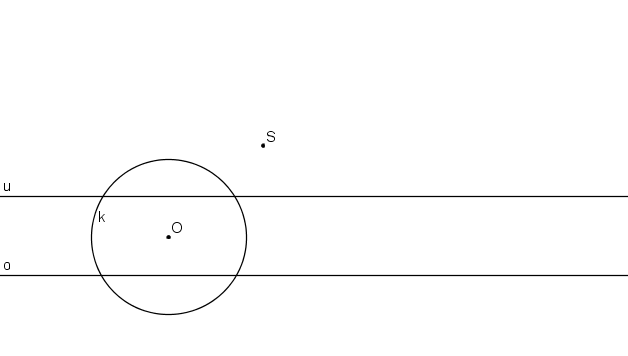
Krokované řešení: Je dán střed kolineace S, osa kolineace o, úběžnice u a kružnice k se středem v bodě O tak, aby úběžnice kružnici protínala ve dvou bodech.
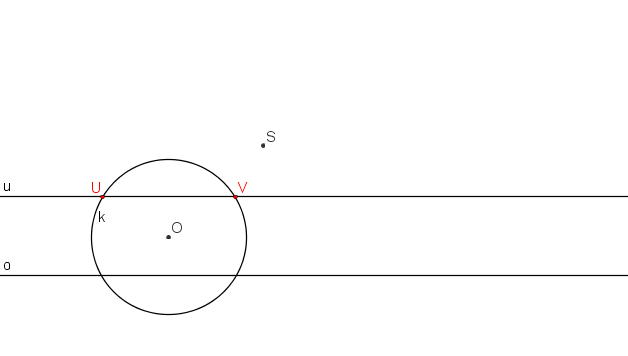
Průsečíky úběžnice u s kružnicí k označme U, V.
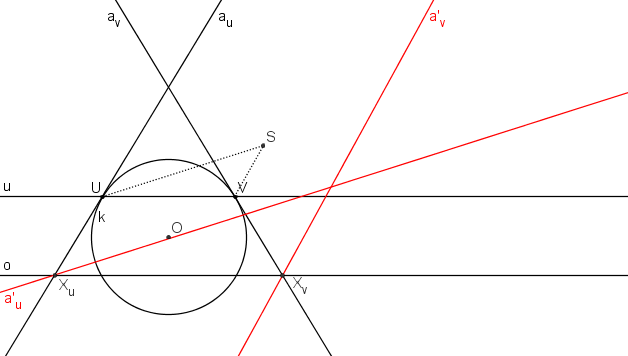
Sestrojíme tečny au, av v bodech U, V ke kružnici k a nalezneme jejich obrazy a´u ( a´u || US), a´v ( a´v || VS). Přímky a´u, a´v jsou asymptoty výsledné hyperboly.
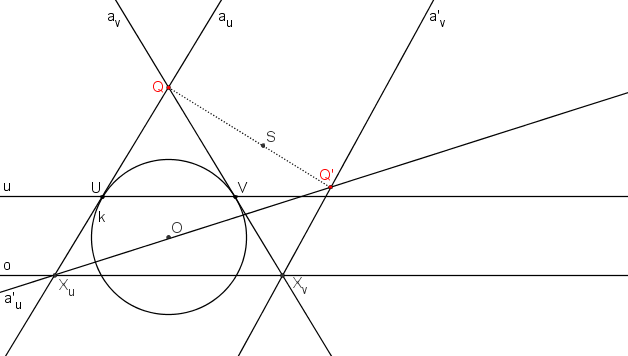
Průsečík asymptot a´u, a´v (ozn. Q´) je středem hyperboly.
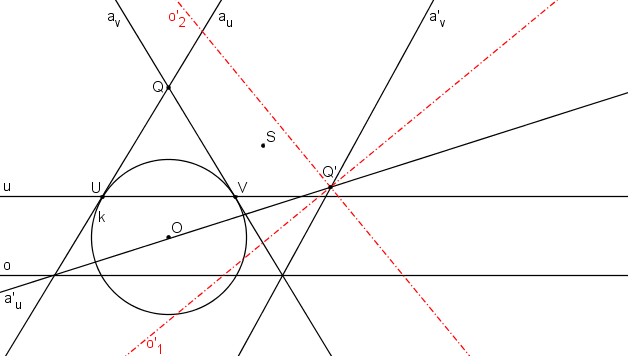
Osy hyperboly o´1, o´2 půlí úhly asymptot.
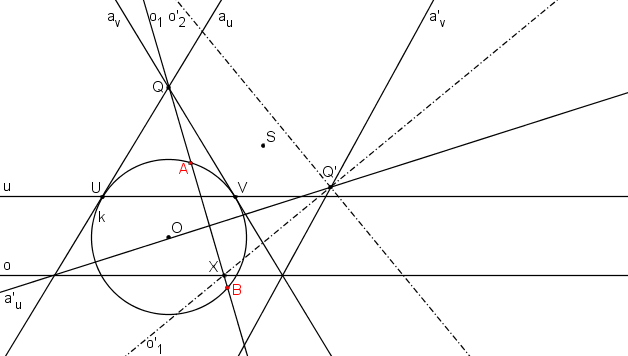
Jako hlavní osu o´1 označíme tu, pro kterou odpovídající přímka o1 protíná kružnici k ve dvou bodech, označme je A, B.
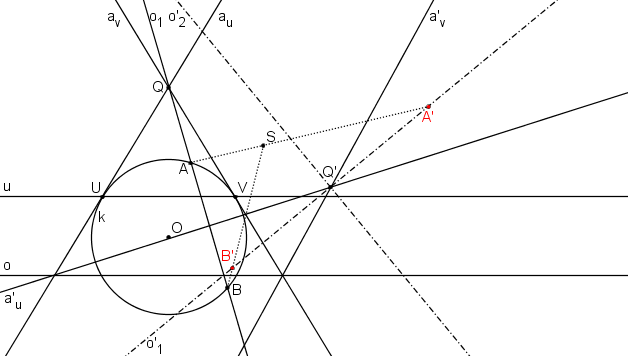
Bodům A, B odpovídají body A´, B´ hyperboly k´ - její hlavní vrcholy.
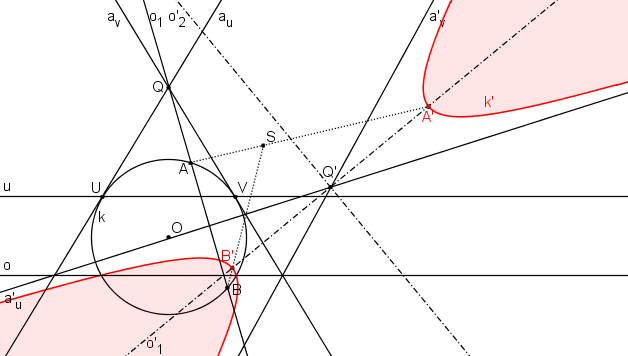
Nyní můžeme vykreslit hyperbolu.
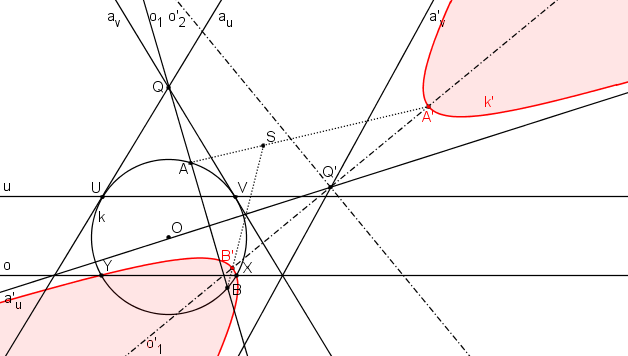
Pokud kružnice k protíná osu kolineace, pak průsečíky X, Y jsou samodružné body a těmito body prochází i výsledná hyperbola.