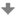Určenost osové afinity
Osová afinita je určena osou afinity o a párem odpovídajících si bodů A, A´. Není třeba znát směr afinity, protože je určen body A, A´. Pokud je OA zadána takto, můžeme hned konstruovat obrazy prvků. Pokud je zadaná jinak, musíme nejprve určit o, A, A´. Osovou afinitu lze určit například těmito způsoby:
- Dvě různoběžné přímky a jejich obrazy
- Tři páry odpovídajících si bodů
- Přímka a bod ležící mimo ni a jejich obrazy
- Dvě rovnoběžné přímky a jejich obrazy a směr afinity
- Osa afinity, směr afinity a charakteristika
- Charakteristika a dva páry odpovídajících si bodů
Následují příklady o tom, jak může být osová afinita zadána a řešení, jak najít osu afinity a pár odpovídajích si bodů.
Úlohu si nejprve zkuste vyřešit sami: Zadání, Řešení. V obrázcích jsou použity jednotné barvy. Zadané prvky modrou barvou, výsledek (osa a pár odpovídajících si bodů) červenou barvou.
Dvě různoběžné přímky a jejich obrazy (a, a´, b, b´)
Krokované řešení: Jsou dány různoběžné přímky a, b a jejich obrazy a´, b´.
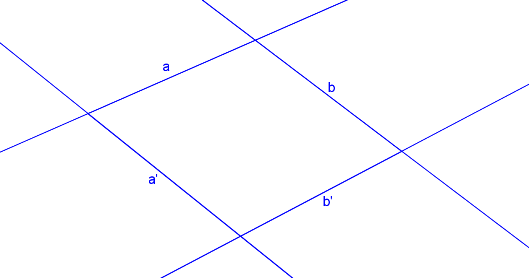
Podle definice víme, že průsečík X odpovídajících si přímek a, a´ leží na ose o, je to samodružný bod.
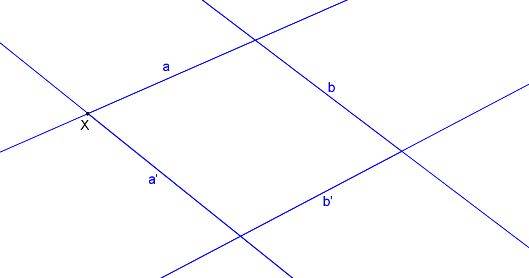
Bod Y je druhým samodružným bodem, je to průsečík přímek b, b´.
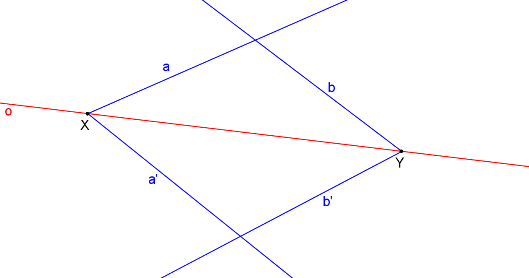
Body X, Y určují osu afinity o.
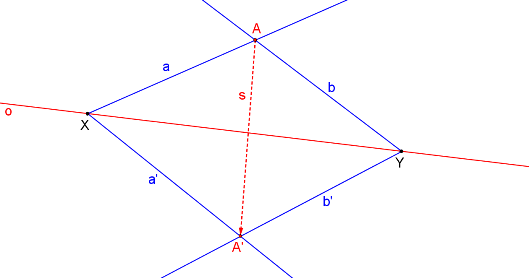
Průsečík přímek a, b se zobrazí na průsečík přímek a´, b´. Tento bod označíme A, A´ a tímto jsme našli odpovídající si body. Příklad je nyní hotov.
Tři páry odpovídajících si bodů (A, A´; B, B´; C, C´)
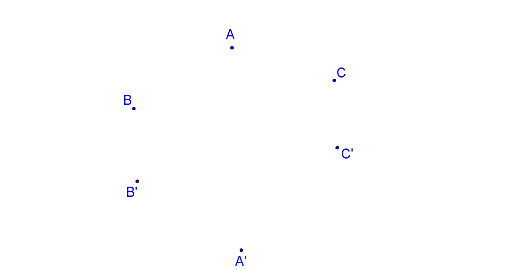
Krokované řešení: Jsou dány tři páry odpovídajících si bodů A, A´; B, B´; C, C´. Aby body A, A´; B, B´; C, C´ byly afinně sdružené, musí být přímky AA´, BB´, CC´ rovnoběžné.
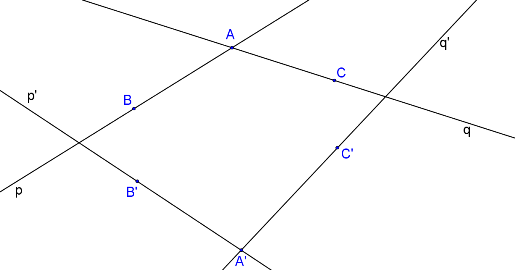
Třemi body lze proložit tři přímky. Ke konstrukci stačí pouze dvě přímky. Například přímka p (určena body A, B) a přímka q (určena body A, C). Přímka p´ je určena body A´, B´, přímka q´ je určena body A´, C´.
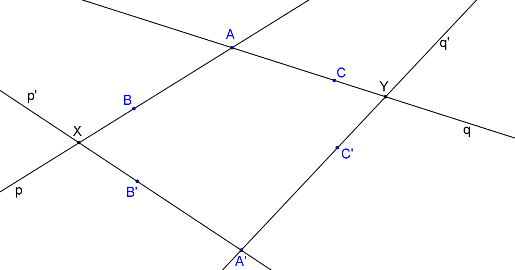
Nyní známe dvě různoběžné přímky a jejich obrazy, takže můžeme postupovat stejně jako v předchozím příkladě. Průsečík přímek p, p´ je samodružný bod X, průsečík přímek q, q´ je samodružný bod Y.
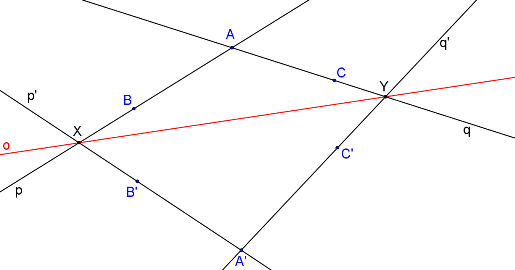
Body X, Y určují osu afinity o.
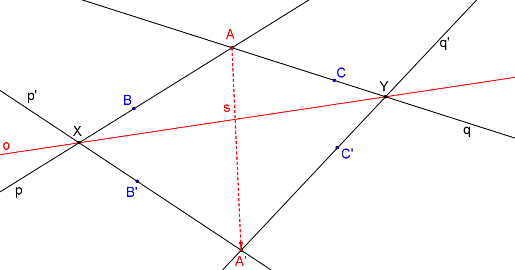
Směr je určen odpovídajícími si body A, A´.
Přímka a bod ležící mimo přímku a jejich obrazy (A, A´; p, p´)
Krokované řešení: Je dána přímka p (p´) a bod A (A´), který na přímce p (p´) neleží.
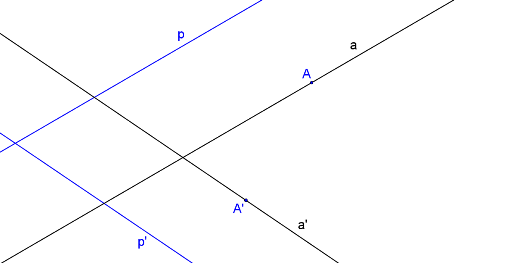
Bodem A vedeme libovolnou pomocnou přímku, která je s přímkou p rovnoběžná nebo různoběžná. Jednodušší a rychlejší je zvolit přímku a, rovnoběžnou s přímkou p, procházející bodem A. Díky zachování rovnoběžnosti a incidence je přímka a´ rovnoběžná s přímkou p´ a prochází bodem A´.
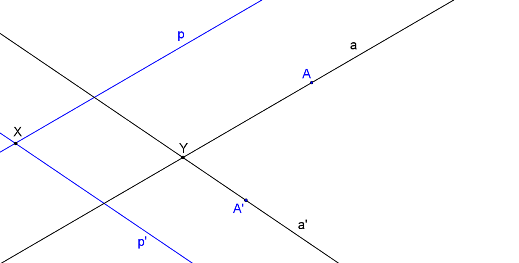
Nyní známě dvě přímky a jejich obrazy. Průsečík přímek p, p´ je samodružný bod X, průsečík přímek a, a´ je samodružný bod Y.
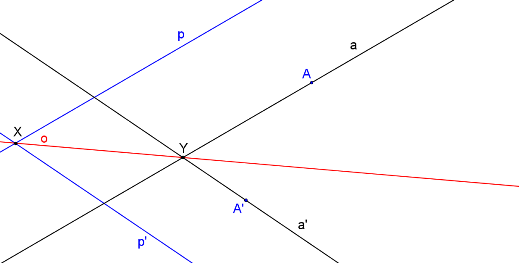
Body X, Y určují osu afinity o.
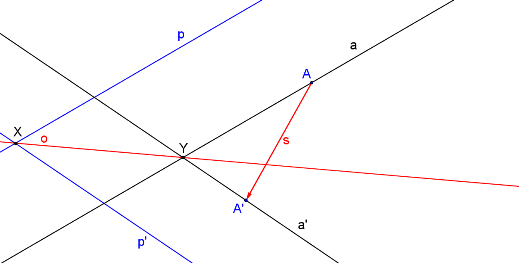
Směr je určen již od začátku body A, A´. Takto je úloha hotová. Může se ale stát, že se průsečík přímek a, a´ nevejde na papír. Úlohu pak musíme řešit jinak: pomocí různoběžné přímky.
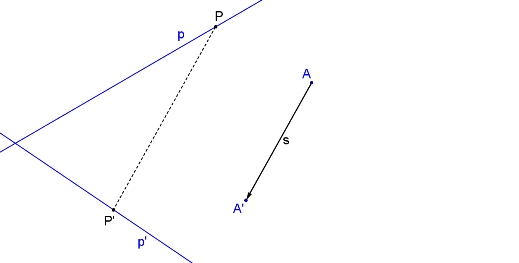
Na přímce p zvolme libovoně bod P. Jeho obraz (P´) leží ve směru afinity AA´ a na přímce p´.
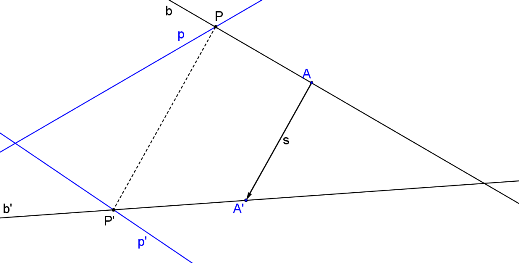
Body AP (A´P´) je určena přímka b (b´).
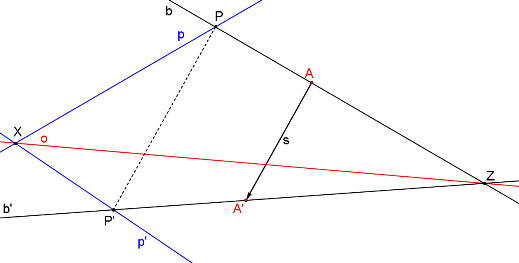
Nyní známe dvě přímky a jejich obrazy. Osa afinity je dána jejich samodružnými body. Bod P již můžeme zvolit tak, aby se průsečík b, b´ vešel na papír.
Dvě rovnoběžné přímky a jejich obrazy (p, p´; q, q´) a směr afinity s
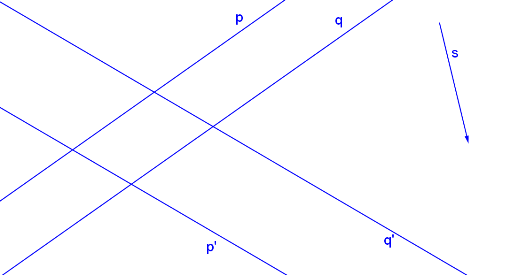
Krokované řešení: Jsou dány přímky p, q a jejich obrazy p´, q´ a směr afinity s, který je s přímkami p, q různoběžný.
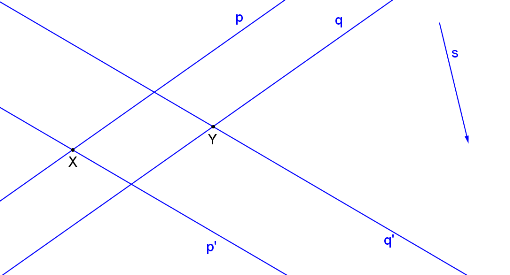
Známe dvě přímky a jejich obrazy. Jednoduše nalezneme samodružné body X, Y jako průsečíky přímek p, p´ a q, q´.
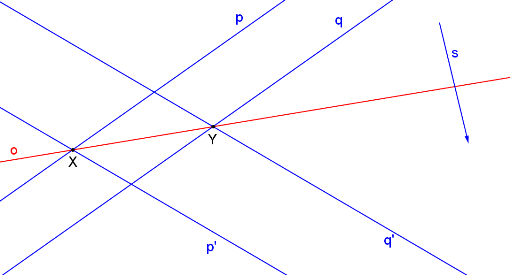
Body X, Y určují osu afinity o.
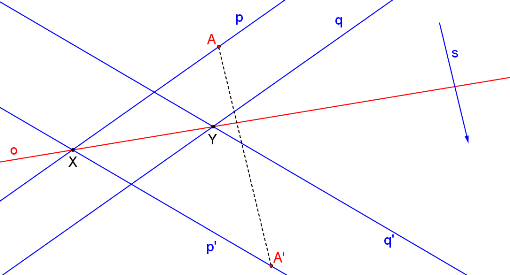
Ještě potřebujeme určit odpovídající si body A, A´. Na přímce p zvolíme libovolně bod A a ve směru afinity s na přímce p´ nalezneme obraz bodu A (A´).
Osa afinity o, směr afinity s a charakteristika \(k = \frac{2}{3}\)
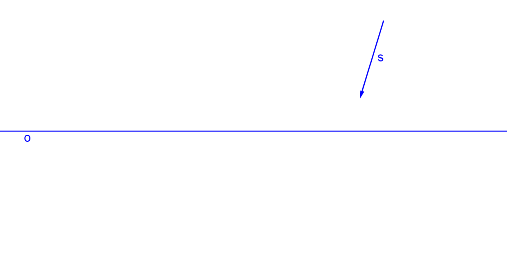
Krokované řešení: Je dána osa afinity o, směr afinity s a charakteristika \(k\).
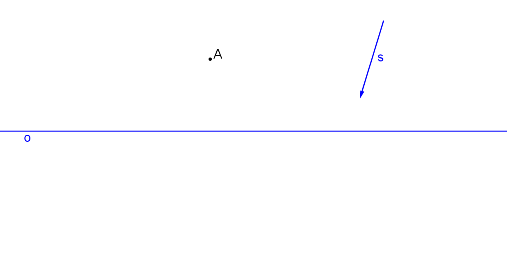
Známe osu i směr, takže hledáme pár odpovídajících si bodů A, A´. Zvolme libovolně bod A.
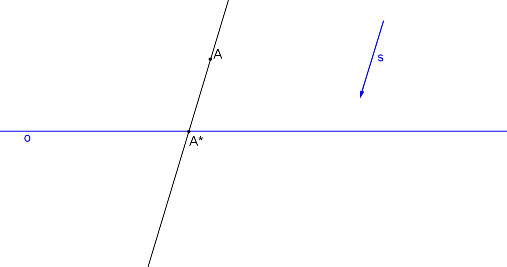
Bodem A vedeme přímku rovnoběžnou se směrem s a na průsečíku této přímky s osou afinity leží bod A*.
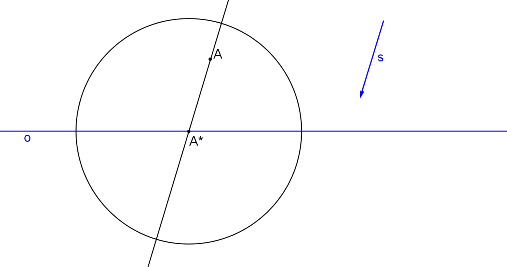
Pro určení bodu A´ se užije charakteristiky \(k = \frac{2}{3}\), \(|k| = \frac{|AA^*|}{|A´A^*|} \). |AA*| = 2 jednotky a |A´A*| = 3 jednotky. Bod A´ leží na kružnici se středem v bodě A* a jeho poloměr \(= \frac{3}{2} . |AA^*| \). \(|A´A^*|= \frac{3}{2} . |AA^*| \)
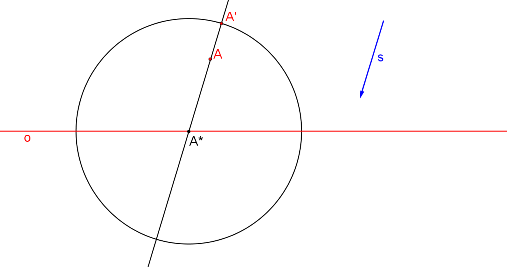
Takto získáváme dvě řešení. Podíváme se, jestli je charakteristika kladná nebo záporná. V našem případě je \(k\) kladná, takže bod A* je vnějším bodem úsečky AA´ a tedy body A, A´ leží v téže polorovině určené osou o.
Charakteristika afinity \(k = - 3\) a dva páry odpovídajících si bodů A, A´; B, B´
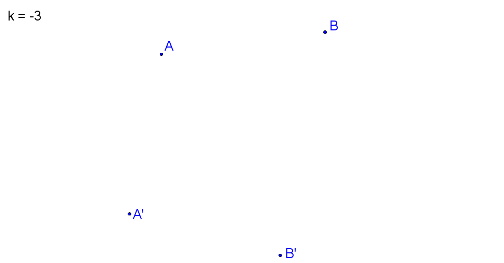
Krokované řešení: Jsou dány body A, A´; B, B´ a charakteristika \(k = - 3\)
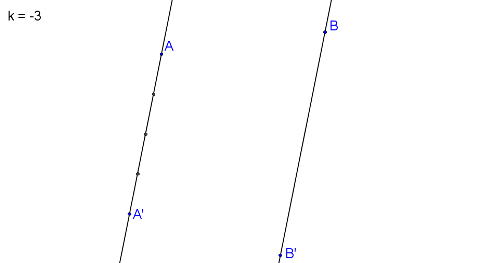
Pro body A, A´ a charakteristiku \(k\) platí: \(\frac{|AA^*|}{|A´A^*|} = | - \frac{3}{1}|\). |AA*| = 3 jednotky, |A´A*| = 1 jednotka. Bod A* je vnitřní bod úsečky A, A´, protože je charakteristika záporná. Rozdělíme proto úsečku A, A´ na 4 díly.
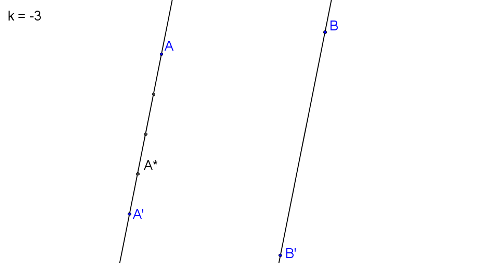
\(|k| = \frac{|AA^*|}{|A´A^*|} = |- \frac{3}{1}|\). Bod A* proto bude blíže bodu A´.
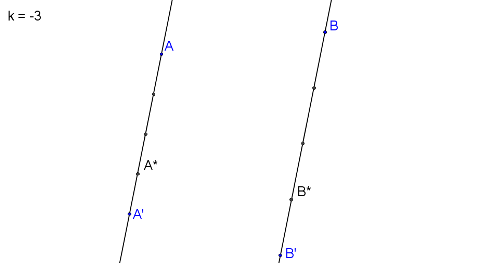
Bod B* zkonstruujeme stejně jako bod A*.
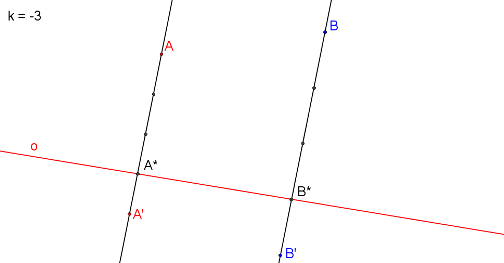
Body A*, B* určují osu o.