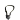\begin{align}
\end{align}
Úloha
Určete charakteristiky a typ kuželosečky dané rovnicí:
- y2 - 8y - 4x + 36 = 0
- 9x2 - 54x + 4y2 + 40y + 145 = 0
- x2 + 8x - 4y2 - 8y - 4 = 0
- x2 - 4x + y2 + 2y - 11 = 0
- Doplníme výraz y2 - 8y na druhou mocninu dvojčlenu y - 4 na:
y2 - 8y + 16 - 16 - 4x + 36 = 0,
(y - 4)2 = 4x - 20,
(y - 4)2 = 4(x - 5).
Rovnice určuje parabolu s vrcholem V[5; 4], řídicí přímkou y = 4 a ohniskem E[6; 4]. - Rovnici upravíme na:
9(x2 - 6x + 9 - 9) + 4(y2 + 10y + 25 - 25) + 145 = 0,
9(x - 3)2 + 4(y + 5)2 - 81 - 100 + 145 = 0,
9(x - 3)2 + 4(y + 5)2 = 36,
\(\dfrac{(x - 3)^{2}}{4} + \dfrac{(y + 5)^{2}}{9} = 1\).
Rovnice určuje elipsu se středem S[3; -5], hlavní poloosou a = 3, vedlejší poloosou b = 2 a výstředností
\(e = \sqrt{5}\).
- Rovnici upravíme na:
x2 + 8x + 16 - 16 - 4(y2 + 2y + 1 - 1) - 4 = 0,
(x + 4)2 - 4(y + 2)2 = 16,
\(\dfrac{(x + 4)^{2}}{16} - \dfrac{(y + 2)^{2}}{4} = 1\).
Rovnice určuje hyperbolu se středem S[-4; -2], hlavní poloosou a = 4, vedlejší poloosou b = 2 a výstředností
\(e = 2\sqrt{5}\).
- Rovnici upravíme na:
x2 - 4x + 4 - 4 + y2 + 2y + 1 - 1 - 11 = 0,
(x - 2)2 + (y + 1)2 = 16.
Jedná se tedy o kružnici se středem S[2; -1] a poloměrem r = 4.
Úloha
Určete střed a poloměr kružnice dané rovnicí x2 - 4x + y2 - 6y + 4 = 0.
- Doplníme výrazy x2 - 4x a y2 - 6y na druhou mocninu dvojčlenů x - 4 a y - 3 a rovnici upravíme:
x2 - 4x + 4 + y2 - 6y + 9 - 4 - 9 + 4 = 0,
(x - 2)2 + (y - 3)2 - 9 = 0,
(x - 2)2 + (y - 3)2 = 9. - Střed zadané kružnice je bod S[2; 3] a její poloměr r = 3.
Úloha
Najděte rovnici kružnice určené body A[3; 3], B[1; 5], C[5; 5].
- Hledaná kružnice se středem S[m; n] a poloměrem r má středovou rovnici:
(x - m)2 + (y - n)2 = r2.
Tři nekolineární body jednoznačně určují kružnici. My využijeme souřadnic bodů A, B, C, které nekolineární jsou a dosadíme je do obecné rovnice hledané kružnice. Získáme tři rovnice o třech neznámých:
(3 - m)2 + (3 - n)2 = r2,
(1 - m)2 + (5 - n)2 = r2,
(5 - m)2 + (5 - n)2 = r2. - Od druhé rovnice odečteme rovnici třetí a vyjádříme hodnotu proměnné m:
(1 - m)2 - (5 - m)2 = 0,
1 - 2m + m2 - 25 + 10m - m2,
8m = 24,
m = 3. - Odečteme od první rovnice druhou a počítáme
(3 - m)2 - (1 - m)2 + (3 - n)2 - (5 - n)2 = 0.
Hodnotu m už známe, dopočítáme tedy n = 5. - Z druhé rovnice teď můžeme po dosazení m = 3, n = 5 dopočítat r2 = 4. Středová rovnice kružnice, určené body A, B a C je:
(x - 3)2 + (y - 5)2 = 4.
Úloha
Určete vzájemnou polohu přímky p: x - y + 1 = 0 a kružnice k: x2 - 6x + y2 - 2y + 1 = 0. Pokud existují, najděte jejich společné body.
- Z obecné rovnice přímky p vyjádříme proměnnou x:
x = y - 1. - Vyjádřenou hodnotu x dosadíme do obecné rovnice kružnice a řešíme kvadratickou rovnici:
(y - 1)2 - 6(y - 1) + y2 - 2y + 1 = 0,
y2 - 2y + 1 - 6y + 6 + y2 - 2y + 1 = 0,
y2 - 5y + 4 = 0,
\(y_{1, 2} = \dfrac{5 \pm \sqrt{25 - 16}}{2} = \dfrac{5 ± 3}{2}\),
y1 = 4, y2 = 1. - Rovnice má dvě řešení. Z toho plyne, že přímka p a kružnice k mají dva společné body. Přímka p je tedy sečna kružnice k. Pro hodnoty y1 a y2 dopočítáme z obecné rovnice přímky p příslušné x1 a x2. Jejich společné body jsou P1[0; 1] a P2[3; 4].
Úloha
Najděte tečny ke kružnici k: x2 - 4x + y2 + 2y - 5 = 0, které procházejí bodem B[7; 4].
- Nejprve upravíme obecnou rovnici kružnice k na její středovou rovnici:
x2 - 4x + 4 + y2 + 2y + 1 - 4 - 1 - 5 = 0,
(x - 2)2 + (y + 1)2 = 10. - Víme, že body dotyku kružnice a hledaných tečen leží na poláře bodu B vzhledem ke k. Polára má rovnici:
(x - 2)(7 - 2) + (y + 1)(4 + 1) = 10,
5x - 10 + 5y + 5 = 10,
5x + 5y - 15 = 0,
x + y - 3 = 0. - Hledáme průsečíky poláry a kružnice k. Z rovnice poláry můžeme vyjádřit x:
x = 3 - y. - Do středové rovnice kružnice k dosadíme za x a řešíme kvadratickou rovnici s neznámou y:
(3 - y - 2)2 + (y + 1)2 = 10,
(1 - y)2 + (y + 1)2 = 10,
1 - 2y + y2 + y2 + 2y + 1 = 10,
y2 = 4. - Dopočítáme y1 = 2, y2 = -2 a příslušné x1 = 1, x2 = 5. Body T1[1; 2] a T2[5; -2] jsou body dotyku. Zbývá určit rovnice tečen.
Obecná rovnice tečny kružnice k v bodě T1 je:
(x - 2)(1 - 2) + (y + 1)(2+ 1) = 10,
x - 3y + 5 = 0.
Obecnou rovnice tečny kružnice k v bodě T2 najdeme stejným způsobem:
(x - 2)(5 - 2) + (y + 1)(-2 + 1) = 10,
3x - y - 17 = 0.
Úloha
Najděte střed, ohniska a hlavní poloosu elipsy dané rovnicí 9x2 + 4y2 + 18x + 24y + 9 = 0.
- Nejprve obecnou rovnici upravíme na rovnici středovou:
9x2 + 18x + 9 + 4y2 + 24y + 36 - 9 - 36 + 9 = 0,
9(x2 + 2x + 1) + 4(y2 + 6y + 9) = 36,
9(x + 1)2 + 4(y + 3)2 = 36,
\(\dfrac{(x + 1)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1\).
Ze středové rovnice snadno určíme jak střed elipsy, tak její hlavní a vedlejší poloosu. Navíc rozpoznáme i její orientaci a jsme tak schopni určit souřadnice ohnisek. - Hlavní poloosa je rovnoběžná s osou y, což nám také napovídá, kde hledat ohniska E a F. Z rovnice určíme hlavní poloosu a = 3, vedlejší poloosu b = 2 a střed elipsy S[-1; -3]. Dopočítáme výstřednost \(e = \sqrt{7}\). Zbývá určit ohniska E a F. Jelikož víme, jak je elipsa orientována, můžeme ohniska jednoduše určit z výstřednosti a souřadnic středu:
E = [-1; -3 + e],
F = [-1; -3 - e],
\(E = [-1; -3 + \sqrt{7}]\),
\(F = [-1; -3 - \sqrt{7}]\).
Úloha
Vyšetřete vzájemnou polohu přímky p: x = 5 + 2t, y = 4 + 4t; t ∈ 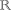 , a elipsy E:
, a elipsy E:
\(\dfrac{(x - 4)^{2}}{2} + \dfrac{(y - 2)^{2}}{8} = 1\).
Určete jejich společné body, pokud existují.
- Vyjdářené souřadnice x a y z parametrické rovnice přímky p dosadíme do středové rovnice elipsy E a získáme
\(\dfrac{(5 + 2t - 4)^{2}}{2} + \dfrac{(4 + 4t - 2)^{2}}{8} = 1\).
4(1 + 2t)2 + (2 + 4t)2 = 8,
4(1 + 4t + 4t2) + (4 + 16t + 16t2) = 8,
32t2 + 32t = 0,
32t(t + 1) = 0,
t1 = 0, t2 = -1. - Vypočítali jsme dvě hodnoty parametru t, které odpovídají průsečíkům přímky p a elipsy e. Přímka p je sečnou elipsy e a protíná ji v bodech P1[5; 4], P2[3; 0].
Úloha
Určete tečnu elipsy \(\dfrac{(x + 3)^{2}}{18} + \dfrac{(y - 4)^{2}}{8} = 1\) v jejím bodě T[0; 2].
- Rovnici tečny k dané elipse můžeme zapsat podle dokázané věty jako
\(\dfrac{(0 + 3)(x + 3)}{18} + \dfrac{(2 - 4)(y - 4)}{8} = 1\),
4(3x + 9) + 9(-2y + 8) = 72,
12x + 36 - 18y + 72 - 72 = 0,
12x - 18y + 36 = 0,
2x - 3y + 6 = 0.
Úloha
Určete rovnice tečen elipsy \(\dfrac{(x - 1)^{2}}{25} + \dfrac{(y + 2)^{2}}{9} = 1\), které procházejí bodem B[6; 1].
- Tečna této elipsy v bodě X[x0; y0] má rovnici \(\dfrac{(x_{0} - 1)(x - 1)}{25} + \dfrac{(y_{0} + 2)(y + 2)}{9} = 1\).
9(x0 - 1)(x - 1) + 25(y0 + 2)(y + 2) = 225.
Má-li procházet bodem B, musí souřadnice bodu B tuto rovnici splňovat:
9(x0 - 1)(6 - 1) + 25(y0 + 2)(1 + 2) = 225,
45(x0 - 1) + 75(y0 + 2) = 225,
45x0 + 75y0 - 120 = 0,
3x0 + 5y0 - 8 = 0. (1)
Tato rovnice vyjadřuje vztah mezi souřadnicemi bodu X[x0; y0], jenž je bodem dotyku elipsy a tečen procházejících bodem B. - Protože víme, že bod X leží na elipse, musí pro jeho souřadnice platit
\(\dfrac{(x_{0} - 1)^{2}}{25} + \dfrac{(y_{0} + 2)^{2}}{9} = 1\).
9(x0 - 1)2 + 25(y0 + 2)2 = 225. (2)
Z (1) plyne
\(x_{0} = \dfrac{8 - 5y_{0}}{3}\).
- Dosadíme do rovnice (2) a počítáme
\(9(\dfrac{8 - 5y_{0}}{3} - 1)^{2} + 25(y_{0} + 2)^{2} = 225\),
\(9\dfrac{(5 - 5y_{0})^{2}}{9} + 25(y_{0} + 2)^{2} = 225\),
25 - 50y0 + 25y02 + 25y02 + 100y0 + 100 = 225,
50y02 + 50y0 - 100 = 0,
y02 + y0 - 2 = 0,
y01 = 1, y02 = -2. - K y01 a y02 můžeme z (1) dopočítat x01 = 1, x02 = 6. To jsou body dotyku tečen elipsy, které procházejí bodem B. Když teď známe body dotyku, můžeme tečny snadno vyjádřit. Jedna z nich má rovnici:
9(1 - 1)(x - 1) + 25(1 + 2)(y + 2) = 225,
75y + 150 = 225,
y = 1.
Druhou dopočítáme obdobně, její rovnice je
x = 6.
Úloha
Najděte vrcholovou rovnici paraboly určené ohniskem E[6; 4] a řídicí přímkou q: x = 2.
- Vrchol hledané paraboly leží na ose paraboly a jeho vzdálenost od ohniska E je rovna jeho vzdálenosti od řídicí přímky q. Souřadnice vrcholu V můžeme určit ze vzdálenosti ohniska a řídící přímky a jejich polohy.
|Eq| = 4, proto můžeme říci, že souřadnice vrcholu V jsou [4; 4]. - Z toho už jednoduše vyjádříme vrcholovou rovnici:
(x - 4)2 = 8(y - 4).
Úloha
Najděte ohnisko, vrchol a řídicí přímku paraboly, která je dána rovnicí x2 - 6x + 4y + 17 = 0.
- Nejprve převedeme obecnou rovnici paraboly na rovnici vrcholovou:
x2 - 6x + 4y + 17 = 0,
(x - 3)2 - 9 + 4y + 17 = 0,
(x - 3)2 = -4y - 8,
(x - 3)2 = -4(y + 2). - Z vrcholové rovnice umíme určit souřadnice vrcholu V[3; -2], vzájemnou polohu její osy a osy y a vzdálenost p řídicí přímky a ohniska, p = 2
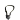 . Rovnice odpovídá parabole na obrázku. Její ohnisko je E[3; -3] a její řídicí přímka q má rovnici:
. Rovnice odpovídá parabole na obrázku. Její ohnisko je E[3; -3] a její řídicí přímka q má rovnici:
y = -1.
Úloha
Napište rovnici tečny paraboly (y + 3)2 = 4(x + 5) v jejím bodě T[1; -1].
- Podle dokázané věty můžeme psát rovnici tečny v bodě paraboly X[x0; y0] jako:
(y0 + 3)(y + 3) = 2(x0 + 5) + 2(x + 5). - Do této rovnice dosadíme souřadnice bodu T a upravíme ji na:
(1 + 3)(y + 3) = 2(-1 + 5) + 2(x + 5),
4y + 12 = 8 + 2x + 10,
2x - 4y + 6 = 0,
x - 2y + 3 = 0.
Úloha
Určete vzájemnou polohu a společné body přímky r: x + 2y + 4 = 0 a paraboly L: (x - 2)2 = 4(y + 5).
- Z rovnice přímky r vyjádříme x = -2y - 4 a dosadíme do rovnice paraboly:
(-2y - 4 - 2)2 = 4(y + 5),
(-2y - 6)2 = 4y + 20,
4y2 + 24y + 36 = 4y + 20,
4y2 + 20y + 16 = 0,
y2 + 5y + 4 = 0. - Diskriminant této rovnice je:
D = 52 - 4⋅1⋅4 = 9.
- Protože je diskriminant kladný, kvadratická rovnice má dvě řešení a parabola p má s přímkou r dva společné body. Přímka r je její sečnou. Dopočítáme souřadnice průsečíků P1 a P2:
y1 = -1 , y2 = -4, x1 = -2, x2 = 4. Tedy P1[-2; -1], P2[4; -4].
Úloha
Najděte střed, ohniska, hlavní vrcholy a asymptoty hyperboly, dané rovnicí: 9x2 - 72x - 16y2 - 32y - 16 = 0.
- Upravíme obecnou rovnici na středovou, ze které dokážeme celou řadu údajů přímo vyčíst.
9(x2 - 8x) - 16(y2 + 2y) - 16 = 0,
9(x2 - 8x + 16) - 9⋅16 - 16(y2 + 2y + 1) + 16⋅1 - 16 = 0,
9(x - 4)2 - 16(y + 1)2 = 144,
\(\dfrac{(x - 4)^{2}}{16} - \dfrac{(y + 1)^{2}}{9} = 1\).
- Z této rovnice určíme souřadnice středu hyperboly, její hlavní a vedlejší poloosu. Střed S má souřadnice S[4; -1], hlavní poloosa a = 4, vedlejší poloosa b = 3. Z a a b dopočítáme výstřednost \(e = \sqrt{16 + 9} = 5\). Ze středové rovnice hyperboly zjistíme, že hlavní osa hyperboly je rovnoběžná s osou x. To nám stačí k určení souřadnic ohnisek E, F a hlavních vrcholů A, B. Jejich souřadnice jsou E[-1; -1], F[9; -1], A[0; -1] a B[8; -1].
- Rovnice asymptot získáme úpravou rovnic \(\dfrac{(x - 4)}{4} = \pm \dfrac{(y + 1)}{3}\).
Ty upravíme na:
a1: 3x - 4y - 16 = 0,
a2: 3x + 4y - 8 = 0.
Úloha
Určete vzájemnou polohu přímky p: 6x + 8y - 14 = 0 a hyperboly H: \(\dfrac{(x - 5)^{2}}{8} - \dfrac{(y + 2)^{2}}{9} = 1\).
Pokud existují, najděte jejich společné body.
- Nejprve z rovnice přímky p vyjádříme x: \(x = \dfrac{14 - 8y}{6}\). (3)
- Dosadíme do rovnice hyperboly a řešíme kvadratickou rovnici:
\(\dfrac{\left(\dfrac{14 - 8y}{6} - 5\right)^{2}}{8} - \dfrac{(y + 2)^{2}}{9} = 1\),
\(9\left(\dfrac{-16 - 8y}{6}\right)^{2} - 8(y + 2)^{2} = 72\),
\(\dfrac{(-16 - 8y)^{2}}{4} - 8(y^{2} + 4y + 4) = 72\),
(-16 - 8y)2 - 32(y2 + 4y + 4) = 288,
256 + 256y + 32y2 - 128y - 128 = 288,
32y2 + 128y - 160 = 0.
y1 = 1, y2 = -5. - Rovnice má dvě řešení, a proto je přímka p sečnou hyperboly H. Jejich průsečíky jsou body P1[1; 1] a P2[9; -5], jejichž x-ové souřadnice získáme dosazením hodnot y1, 2 do rovnice (3).
Úloha
Napište rovnici tečny hyperboly 4x2 - 5y2 - 24x - 10y + 11 = 0 v jejím bodě T[-2; 3].
- Obecnou rovnici hyperboly převedeme na rovnici středovou:
4(x2 - 6x + 9 - 9) - 5(y2 + 2y + 1 - 1) = -11,
4(x - 3)2 - 5(y + 1)2 - 36 + 5 = -11,
4(x - 3)2 - 5(y + 1)2 = 20,
\(\dfrac{(x - 3)^{2}}{5} - \dfrac{(y + 1)^{2}}{4} = 1\). - Rovnici tečny k hyperbole v bodě T, určíme z dokázané věty. Je to:
\(\dfrac{(-2 -3)(x - 3)}{5} - \dfrac{(3 + 1)(y + 1)}{4} = 1\),
-20(x - 3) - 20(y + 1) = 20,
-20x + 60 - 20y - 20 = 20,
x + y - 1 = 0.
Úloha
Určete rovnici kulové plochy vepsané do krychle ABCDEFGH, když A[3; 1; 1], B[3; 3; 1], C[1; 3; 1], D[1; 1; 1], E[3; 1; 3], F[3; 3; 3], G[1; 3; 3], H[1; 1; 3].
- Poloměr r hledané kulové plochy odpovídá polovině velikosti hran krychle, můžeme použít například hranu AB. Střed vepsané kulové plochy je středem úhlopříčky AG.
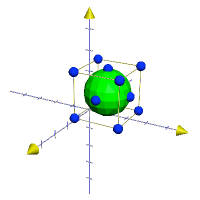
Obrázek k úloze
\(S = S_{AG} = \left[\dfrac{3 + 1}{2}; \dfrac{1 + 3}{2}; \dfrac{1 + 3}{2}\right] = [2; 2; 2]\). - Rovnice kulové plochy se pak dá zapsat jako:
(x - 2)2 + (y - 2)2 + (z - 2)2 = 4.
Úloha
Najděte společné body přímky p(A; u) a kulové plochy dané rovnicí (x - 2)2 + (y - 1)2 + (z + 1)2 = 36, je-li A[7; 9; 4] a u = (-3; -4; -1).
- Nejprve si vyjádříme přímku p parametricky.
p:
x = 7 - 3t,
y = 9 - 4t,
z = 4 - t; t ∈  .
. - Vyjádřené souřadnice dosadíme do rovnice sféry a získáme:
(7 - 3t - 2)2 + (9 - 4t - 1)2 + (4 - t + 1)2 = 36,
26t2 - 104t + 78 = 0,
t2 - 4t + 3 = 0. - Kořeny této kvadratické rovnice jsou:
t1 = 3, t2 = 1.
Rovnice má dvě řešení, a proto můžeme říci, že přímka p je sečnou zadané sféry. Jejich průsečíky jsou body , které v parametrické rovnici přímky p odpovídají vypočítaným hodnotám parametrů t1 a t2,
P1[-2; -3; 1], P2[4; 5; 3].
Úloha
Najděte průnik kulové plochy (x - 4)2 + (y - 1)2 + (z + 3)2 = 32 s rovinou yz .
.
- Rovina yz má rovnici x = 0, rovnice kulové plochy je (x - 4)2 + (y - 1)2 + (z + 3)2 = 32. Hledáme řešení soustavy:
(x - 4)2 + (y - 1)2 + (z + 3)2 = 32,
x = 0. - Vyjádřené x můžeme dosadit do rovnice kulové plochy a získáme
(-4)2 + (y - 1)2 + (z + 3)2 = 32,
(y - 1)2 + (z + 3)2 = 16. - Průnikem roviny yz a kulové plochy je kružnice ležící v rovině yz. Jejím středem je bod S[0; 1; -3] a poloměr r = 4.
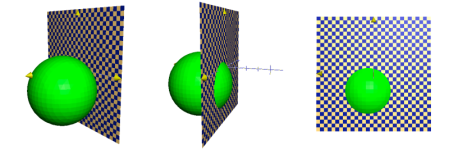
Obrázek k úloze
![]() , a elipsy E:
, a elipsy E: