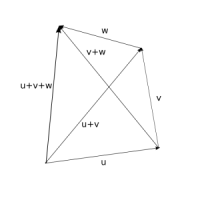
Sčítání vektorů
Operace s vektory jsou poměrně jednoduché. První a nejjednodušší z nich je sčítání dvou vektorů.
Mějme dva vektory u = B – A a v = E – D. Umístíme-li počáteční bod vektoru v do bodu B, pak v = C - B. Součet vektorů u + v = C - A.
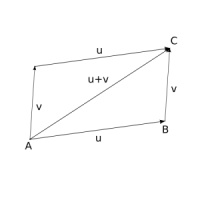
Pro každé dva vektory v rovině u = (u1; u2), v = (v1; v2), resp. v prostoru u = (u1; u2; u3), v = (v1; v2; v3), platí
u + v = (u1 + v1 ; u2 + v2),
resp.
u + v = (u1 + v1 ; u2 + v2 ; u3 + v3).
Vypočítejte součet vektorů u a v, jestliže u = (3; 5) a v je určen orientovanou úsečkou AB, je-li A[-1; 2], B[3; -1].
- u = (3; 5),
- v = (3 + 1; -1 - 2) = (4; -3),
- u + v = (3 + 4; 5 - 3) = (7; 2).
Pro každé tři vektory u, v, w (v rovině nebo v prostoru) platí
- u + v = v + u;
- (u + v) + w = u + (v + w).
Je dán vektor u = B – A. Vektor A – B nazýváme opačný vektor k vektoru u a označujeme jej -u.
Pro každý vektor u v rovině, resp. v prostoru, platí:
- u + (-u) = o.
- Jestliže u = (u1; u2), resp. u = (u1; u2; u3) v prostoru, pak pro souřadnice vektoru -u, platí -u = (-u1; -u2), resp. v prostoru -u = (-u1; -u2; -u3).
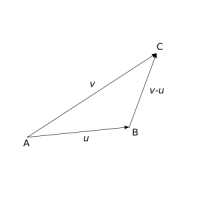
Jsou-li dány vektory u, v, potom vektor w = v + (-u) nazýváme rozdíl vektorů v a u.
Zapisujeme w = v - u.
Vypočítejte součet a rozdíl vektorů u = (3; 1; 5) a v = (2; -2; 1).
- u + v = (3 + 2; 1 - 2; 5 + 1) = (5; -1; 6),
- u - v = u + (-v) = (3 - 2; 1 + 2; 5 - 1) = (1; 3; 4).