Parabola
Parabola je kuželosečka, která vznikne průnikem rotační kuželové plochy s rovinou, která neprochází jejím vrcholem a která je rovnoběžná s právě jednou přímkou této kuželové plochy.

V rovině je dán bod F a přímka q, která jím neprochází. Množina všech bodů roviny, které mají stejnou vzdálenost od bodu F a od přímky q, se nazývá parabola. Bod F se nazývá ohnisko, přímka q řídicí přímka paraboly.
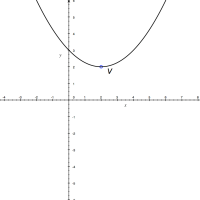
Bod V, na obr. 5.14, je jediný bod paraboly ležící na její ose o. Nazýváme jej vrchol paraboly. Vzdálenost ohniska paraboly od její řídicí přímky budeme označovat jako p.
Rovnice
(x - m)2 = ±2p(y - n), resp. (y - n)2 = ±2p(x - m), kde p > 0,
se nazývají vrcholové rovnice paraboly s vrcholem V[m; n] a ohniskem E[m; n ± p/2], resp. E[m ± p/2; n].
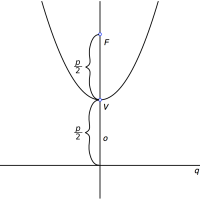
Z vrcholové rovnice můžeme určit polohu vrcholu, ohniska a řídicí přímky paraboly. Na obr. 5.15 jsou zleva doprava části parabol s rovnicemi y = 2(x - 1)2, y = -2(x - 1)2, x = -2(y -1)2 a x = 2(y - 1)2.
Paraboly (x - m)2 = ±2p(y - n) mají osu rovnoběžnou s osou y. Parabola je „otevřená‟ ve směru kladné poloosy y, pokud má rovnici (x - m)2 = 2p(y - n). Parabola je „otevřená‟ ve směru záporné poloosy y, pokud má rovnici (x - m)2 = -2p(y - n).
Paraboly (y - n)2 = ±2p(x - m) mají osu rovnoběžnou s osou x. Parabola je „otevřená‟ ve směru záporné poloosy x, pokud má rovnici (y - n)2 = -2p(x - m). Parabola je „otevřená‟ ve směru kladné poloosy x, pokud má rovnici (y - n)2 = 2p(x - m).
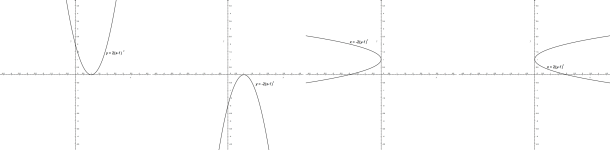
Najděte vrcholovou rovnici paraboly určené ohniskem E[2; 4] a řídicí přímkou q: y = -2.
- Vrchol V hledané paraboly leží mezi bodem E a přímkou q. Platí, že V ∈ o a 2|EV| = 2|Vq| = p.
Ze vzdálenosti E a q a jejich polohy viz obr. 5.16, můžeme určit jeho souřadnice. Protože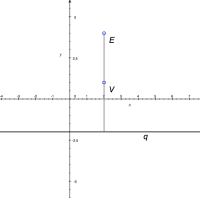 Obr. 5.16: Obrázek k příkladu
Obr. 5.16: Obrázek k příkladu
|Eq| = 6, můžeme říci, že souřadnice vrcholu V jsou [2; 1]. Z toho už jednoduše vyjádříme vrcholovou rovnici:
(x - 2)2 = 12(y - 1).
Rovnice paraboly ve tvarech x2 + 2rx + 2sy + t = 0 a y2 + 2sx + 2ry + t = 0; r ≠ 0, r, s, t ∈ ![]() , se nazývají obecné rovnice paraboly.
, se nazývají obecné rovnice paraboly.
Určete obecnou rovnici paraboly s vrcholem V[2; -1], jejíž řídicí přímka je osa y.
- Vrcholovou rovnici určíme ze souřadnic vrcholu paraboly a velikosti koeficientu p, který odpovídá dvojnásobku vzdálenosti vrcholu od řídicí přímky, p = 4.
Je ještě potřeba vzít v úvahu, polohu vrcholu V vůči řídicí přímce paraboly. Naše parabola je „otevřená‟ ve směru kladné poloosy x a její vrcholová rovnice je:
(y + 1)2 = 8(x - 2). - Obecnou rovnici získáme roznásobením a upravením vrcholové rovnice paraboly:
y2 + 2y + 1 = 8x - 16,
y2 - 8x + 2y + 17 = 0.
Najděte ohnisko, vrchol a řídicí přímku paraboly, která je dána rovnicí x2 - 4x - 4y + 12 = 0.