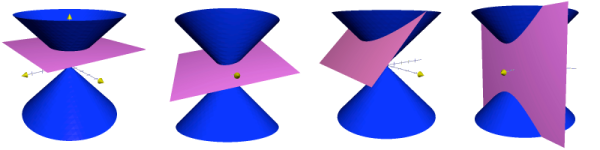
Za jistých okolností může být průnikem roviny a kuželové plochy bod, přímka nebo dvě přímky. Tyto útvary se proto někdy označují jako singulární kuželosečky. Kružnice, elipsa, parabola a hyperbola jsou potom označovány jako kuželosečky regulární.
Kuželosečky
V předchozích kapitolách jsme se naučili vyjadřovat základní geometrické útvary rovnicemi a řešit s nimi různé úlohy. Svět geometrie ale nejsou jen přímky, úsečky, vektory atd. V rovině kromě přímek existují i další křivky a v prostoru jsou i jiné plochy než jen roviny. V této kapitole se budeme zabývat křivkami, které se souhrnně nazývají kuželosečky. Jsou to kružnice, elipsa, parabola a hyperbola. Ukážeme si, jak je lze matematicky vyjádřit a naučíme se řešit další úlohy.
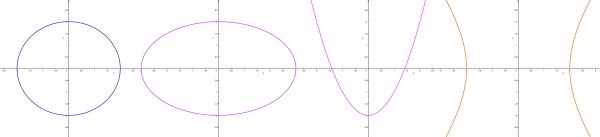
Kuželosečky, jak již název napovídá, mají společný původ. Získáme je jako řez rotační kuželové plochy rovinou.
rovinou.