Kružnice je speciální případ elipsy, jejíž ohniska splývají s jejím středem. Pro každý bod X této elipsy platí |EX| + |FX| = 2|SX| = 2r.
Elipsa
Elipsa vznikne řezem rotační kuželové plochy rovinou, která neprochází jejím vrcholem a pro jejíž odchylku φ od osy rotace kuželové plochy platí: φ ∈ (α; 90°), kde α je odchylka tvořících přímek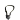 kuželové plochy od její osy.
kuželové plochy od její osy.

Množina všech bodů X roviny, pro které se součet |XE| + |XF|, vzdáleností bodu X od daných bodů E, F této roviny, rovná danému číslu většímu než |EF|, se nazývá elipsa. Body E a F se nazývají ohniska elipsy.
Na obr. 5.8 jsou elipsy s ohnisky E, F. Bod S se nazývá střed elipsy. Body A, B, ležící na přímce EF nazýváme hlavní vrcholy elipsy, přímku AB potom hlavní osa elipsy. Body C, D se nazývají vedlejší vrcholy elipsy a přímka CD vedlejší osa elipsy. Vzdálenost a hlavního vrcholu elipsy a jejího středu nazýváme hlavní poloosa elipsy a vzdálenost b vedlejšího vrcholu a středu analogicky vedlejší poloosa elipsy. Vzdálenost e, ohniska a středu elipsy nazýváme výstřednost nebo také excentricita elipsy. Z obr. 5.8 plyne vztah mezi výstředností a hlavní a vedlejší poloosou a2 = b2 + e2. To platí, protože |EA| + |FA| = e + a + a - e = 2a, a tedy |ED| + |FD| = 2a.
Určete výstřednost elipsy s hlavním vrcholem A[-1; 1], vedlejším vrcholem B[4; -2] a středem S[4; 1].
- Ze zadání můžeme určit hlavní a vedlejší poloosu a, b dané elipsy. Vime, že
a = |AS| a b = |BS|.
\(a = \sqrt{(4 - (-1))^{2} + (1 - 1)^2} = \sqrt{5^{2}} = 5\),
\(b = \sqrt{(4 - 4)^{2} + (1 - (-2)^{2}} = \sqrt{3^{2}} = 3\). - Ze vztahu a2 = b2 + e2 dopočítáme výstřednost e:
e2 = a2 - b2 = 52 - 32 = 25 - 9 = 16,
e = ±4.
Protože výstřednost je vzdálenost ohniska od středu, může to být jen nezáporné číslo, tedy e = 4.
Rovnice
\(\dfrac{(x - m)^2}{a^2} + \dfrac{(y - n)^{2}}{b^{2}} = 1; a, b > 0\)se nazývá středová rovnice elipsy se středem S[m; n] a poloosami a, b.
Pro ohniska E[e1; e2], F[f1; f2] elipsy z definice platí následující. Je-li a ≥ b, platí e2 = f2 = n, e1 = m - e a f1 = m + e. Je-li a < b platí e1 = f1 = m, e2 = n + e, f2 = n - e, kde
\(e = \sqrt{a^{2} - b^{2}}.\)Pokud je a ≥ b, tak středová rovnice určuje elipsu, jejíž hlavní osa je rovnoběžná s osou x a a je její hlavní poloosa viz obr. 5.8 vlevo. Je-li a < b, pak středová rovnice elipsy určuje elipsu jejíž hlavní osa je rovnoběžná s osou y a její hlavní poloosa je b viz obr. 5.8 vpravo.
Najděte středovou rovnici elipsy se středem S[2; 2], výstředností e = 4 a hlavním vrcholem A[-3; 2].
- Abychom mohli napsat rovnici elipsy, potřebujeme znát ještě její hlavní a vedlejší poloosu. Nejprve vypočítáme hlavní poloosu |SA|:
\(|SA| = \sqrt{(-3 -2)^{2} + (2 - 2)^{2}} = \sqrt{25} = 5.\) - Vedlejší poloosu b vypočítáme z hlavní poloosy a výstřednosti:
b2 = a2 - e2,
b = 3. - Zadaná elipsa má hlavní osu rovnoběžnou s osou x. To je vidět ze souřadnic bodů A a S na obr. 5.9. Body A, S mají stejnou y-ovou souřadnici a liší se jejich souřadnice x-ová.
Hledanou středovou rovnici elipsy pak zapíšeme jako: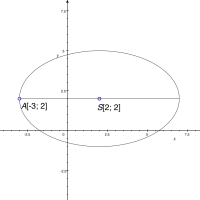 Obr. 5.9: Obrázek k příkladu
Obr. 5.9: Obrázek k příkladu
\(\dfrac{(x - 2)^{2}}{25} + \dfrac{(y - 2)^{2}}{9} = 1\)
Rovnice elipsy ve tvaru px2 + qy2 + 2rx + 2sy + t = 0; p, q, r, s, t ∈ ![]() , p⋅q > 0, se nazývá obecná rovnice elipsy.
, p⋅q > 0, se nazývá obecná rovnice elipsy.
Ne každá rovnice px2 + qy2 + 2rx + 2sy + t = 0; p⋅q > 0, je rovnicí elipsy - to je obdobné jako u kružnice a její obecné rovnice.
Určete střed, ohniska a hlavní poloosu elipsy dané rovnicí 25x2 + 9y2 + 150x - 36y + 36 = 0.
- Nejprve obecnou rovnici upravíme na rovnici středovou:
25x2 + 9y2 + 150x - 36y + 36 = 0,
25x2 + 150x + 9y2 - 36y + 36 = 0,
25(x2 + 6x) + 9(y2 - 4y) + 36 = 0,
25(x2 + 6x + 9 - 9) + 9(y2 - 4y + 4 - 4) + 36 = 0,
25(x + 3)2 - 225 + 9(y - 2)2 - 36 + 36 = 0,
25(x + 3)2 + 9(y - 2)2 = 225,
\(\dfrac{25(x + 3)^{2}}{225} + \dfrac{9(y - 2)^{2}}{225} = 1\),
\(\dfrac{(x + 3)^{2}}{9} + \dfrac{(y - 2)^{2}}{25} = 1\). - Ze středové rovnice snadno určíme jak střed elipsy, tak její hlavní osu a vedlejší poloosu. Navíc rozpoznáme i orientaci její hlavní osy viz obr. 5.10.
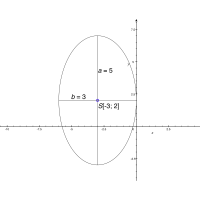 Obr. 5.10: Obrázek k příkladu
Obr. 5.10: Obrázek k příkladu - Hlavní osa je rovnoběžná s osou y, což nám také napovídá, kde hledat ohniska E a F. Z rovnice určíme hlavní poloosu a = 5,
vedlejší poloosu b = 3 a střed elipsy S[-3; 2]. Dopočítáme výstřednost e = 4 a zbývá určit ohniska E a F.
Jelikož víme, že hlavní osa elipsy je rovnoběžná s osou y, můžeme ohniska jednoduše určit za pomocí výstřednosti a souřadnic středu:
E = [-3; 2 + e] = [-3; 6],
F = [-3; 2 - e] = [-3; -2].
Najděte obecnou rovnici elipsy, která má střed S[2; 1], hlavní vrchol A[-3; 1] a ohnisko E[-2; 1].
