Z definice báze plyne, že ani jeden z vektorů báze nemůže být nulový.
Vektorový součin
Vektorový součin je další operace s vektory. Už víme, že výsledek skalárního součinu dvou vektorů je číslo, výsledkem vektorového součinu je vektor. Narozdíl od skalárního součinu, je vektorový součin definován jen pro vektory v prostoru. Než si jej zavedeme, je potřeba zmínit se o pravo- a levotočivých bázích v prostoru, které nám umožní určit orientaci vektoru, který je výsledkem vektorového součinu.
Pravotočivá a levotočivá báze
Mějme tři libovolné vektory v prostoru. Zvolíme si takové umístění těchto vektorů, aby jejich počáteční body byly identické. Každá trojice vektorů, jejichž umístění neleží v jedné rovině, je bází v prostoru.
Bázi v prostoru určenou vektory a, b a c budeme označovat (a, b, c).
Pomocí nám již známých pojmů by se to dalo vyjádřit jako:
Trojice vektorů v prostoru tvoří bázi v prostoru právě tehdy, když se žádný z vektorů nedá vyjádřit jako lineární kombinace zbývajících dvou vektorů.
Zda je báze (a, b, c) pravo- nebo levotočivá, rozlišíme takto:
Zvolíme takové umístění vektorů a, b, c,
aby jejich počáteční bod byl stejný. Položíme pravou ruku na pomyslnou rovinu určenou vektory a, b tak, aby pokrčené prsty ruky udávaly směr od vektoru
a k b (nejkratším směrem). Vztyčený palec pak může směrovat do stejného
poloprostoru jako vektor c. V tom případě se báze nazývá pravotočivá. Pokud vztyčený palec ukazuje do
opačného poloprostoru, nazveme bázi levotočivou (kdybyste místo pravé ruky teď použili ruku levou, tak její palec ukazuje do
stejného poloprostoru jako vektor c). Na obr. 2.6 vlevo tvoří vektory a, b, c pravotočivou bázi, vpravo potom levotočivou.
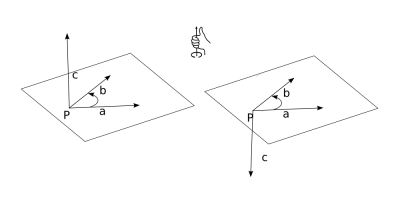
Vektorový součin dvou vektorů, jejichž nějaké umístění leží na jedné přímce, je nulový vektor. Vektorový součin dvou vektorů u, v, jejichž žádné umístění neleží na jedné přímce, je vektor w, který má tyto vlastnosti:
- vektor w je kolmý k oběma vektorům u, v;
- vektory u, v, w tvoří pravotočivou bázi;
- |w| = |u||v|sinα, kde α je odchylka vektorů u a v.
Vektorový součin w vektorů u, v značíme u × v, tj. w = u × v.
Všiměte si, že vektorový součin je definován jen prostoru, a že výsledkem vektorového součinu dvou vektorů je vektor.
Pro souřadnice vektorového součinu w vektorů u = (u1; u2; u3) a v = (v1; v2; v3) platí:
w = u × v = (u2v3 - u3v2; u3v1 - u1v3; u1v2 - u2v1).
Pro snadné zapamatování výše zmíněného vzorce se využívá následující pomůcka:
Zapíšete souřadnice vektorů pod sebe, přičemž začnete u prostřední a skončíte znovu prostřední. Čáry mezi souřadnicemi vyjadřují násobení. Čára \ odpovídá kladnému znaménku, / pak zápornému znaménku.
| u2 |  | u3 |  | u1 |  | u2 |
| v2 | v3 | v1 | v2 | |||
| u2v3 - v2u3 | u3v1 - v3u1 | u1v2 - v1u2 |
Vypočítejte vektorový součin vektorů u = (2; 3; 1) a v = (1; 2; 1)
- u × v = (3·1 - 2·1; 1·1 - 1·2; 2·2 - 1·3),
- u × v = (1; -1; 1).
Smíšený součin
Spojení vektorového a skalárního součinu se nazývá smíšený součin. Smíšený součin je stejně jako vektorový součin definován pouze v prostoru.
Smíšený součin vektorů a, b, c je číslo (a × b)∙c.
Smíšený součin vektorů je číslo (z vektorového součinu vznikne vektor a skalární součin dvou vektorů je číslo). Absolutní hodnota smíšeného součinu vektorů a, b, c je rovna objemu rovnoběžnostěnu, který tyto tři vektory určují, je-li jejich umístění zvoleno tak, že mají společný počáteční bod (viz obr. 2.7).
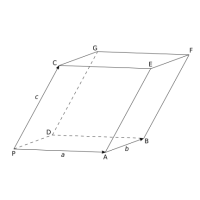
Vypočítejte smíšený součin (u × v)⋅w vektorů u = (5; 1; 0), v = (1; 4; 1) a w = (1; 0; 3).
- Řešení příkladu rozdělíme do dvou kroků. Nejprve spočítáme u × v a získaný vektor skalárně vynásobíme vektorem w.
- (u × v) = (1⋅1 - 4⋅0; 0⋅1 - 1⋅5; 5⋅4 - 1⋅1) = (1; -5; 19),
- (u × v)w = (1; -5; 19)(1; 0; 3) = 1 + 57 = 58.
Spočtěte objem rovnoběžnostěnu ABCDEFGH, kde A[1; 0; 0], B[6; 0; 0], C[6; -4; 0], D[1; -4; 0], E[1; 0; 5], F[6; 0; 5], G[6; -4; 5], H[1; -4; 5].
