Vzájemná poloha elipsy a přímky
V rovině mohou nastat tři různé vzájemné polohy elipsy E a přímky p: nemají žádný společný bod, mají jeden společný bod nebo mají dva společné body.
- p ∩ E = ∅
Přímka p leží vně elipsy E. Nazýváme ji vnější přímka elipsy. - p ∩ E = {P}
Přímka p se elipsy E dotýká v bodě P. Přímku p nazýváme tečna elipsy E. - p ∩ E = {X, Y}
Přímka elipsou prochází a protíná ji v bodech X a Y. Přímku p nazýváme sečna elipsy E.

Určete vzájemnou polohu přímky p: x - 3y + 1 = 0 a elipsy E:
\(\dfrac{x^{2}}{4} + y^{2} = 1\).- Z rovnice přímky p vyjádříme x = 3y - 1 a dosadíme do středové rovnice elipsy E. Získáme kvadratickou rovnici
\(\dfrac{(3y - 1)^{2}}{4} + y^{2} = 1\)
(3y - 1)2 + 4y2 = 4,
9y2 - 6y + 1 + 4y2 - 4 = 0,
13y2 - 6y - 3 = 0. - Kořeny této kvadratické rovnice odpovídají y-ové souřadnici společných bodů p a E.
Z diskriminantu D zjistíme, kolik jich je, a podle toho i vzájemnou polohu. Je-li D < 0, přímka je vnější přímkou elipsy. Je-li D = 0, přímka je tečnou elipsy a nakonec, je-li D > 0, přímka elipsu protíná ve dvou bodech a je její sečnou. V našem případě
D = (-6)2 - 4⋅13⋅(-3) = 36 + 156 = 192.
Diskriminant je kladný a přímka p má proto s elipsou E dva společné body. Přímka p je sečnou elipsy E.
Vyšetřete vzájemnou polohu přímky p: x = 3 + t, y = 2 - 2t; t ∈ ![]() , a elipsy
, a elipsy
\(\dfrac{x^{2}}{4} + \dfrac{y^{2}}{9} = 1\).
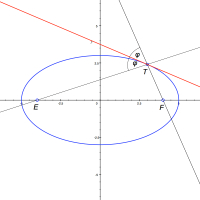
Pokud byste někdy chtěli zkonstruovat tečnu elipsy v nějakém jejím bodě vězte, že tečna k elipse s ohnisky E, F v jejím libovolném bodě T je ta osa úhlu přímek ET, EF, která neprochází úsečkou EF.
Určete tečnu elipsy
\(\dfrac{(x - 2)^{2}}{10} + \dfrac{(y - 3)^{2}}{40} = 1\)
v bodě T[3; 9].
- Rovnici tečny k dané elipse můžeme zapsat podle dokázané věty jako
\(\dfrac{(3 - 2)(x - 2)}{10} + \dfrac{(9 - 3)(y - 3)}{40} = 1\),
\(\dfrac{(x - 2)}{10} + \dfrac{6(y - 3)}{40} = 1\),
4(x - 2) + 6(y - 3) = 40,
4x - 8 + 6y - 18 - 40 = 0,
4x + 6y - 66 = 0,
2x + 3y - 33 = 0.
Určete rovnice tečen elipsy
\(\dfrac{(x + 1)^{2}}{32} + \dfrac{(y - 2)^{2}}{2} = 1\),
které jsou kolmé k přímce p: 4x - y + 5 = 0.