Vzájemná poloha kružnice a přímky
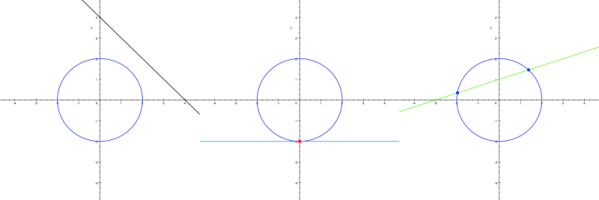
V rovině mohou nastat tři různé vzájemné polohy kružnice k a přímky p. Podobně jako u vzájemné polohy dvou přímek je rozlišujeme podle toho, kolik mají společných bodů. Mohou nastat tyto případy: nemají žádný společný bod, mají jeden společný bod nebo mají dva společné body.
- p ∩ k = ∅
Přímka p leží vně kružnice k a nazýváme ji vnější přímka kružnice. - p ∩ k = {P}
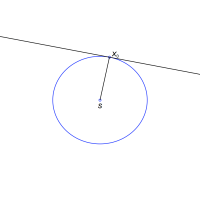
Přímka p se kružnice k dotýká v bodě P. Přímku p nazýváme tečnou kružnice k. - p ∩ k = {X, Y}
Přímka kružnici protíná v bodech X a Y. Přímku p nazýváme sečnou kružnice k.
Najděte průsečíky přímky p(A, u) a kružnice (x - 3)2 + (y - 2)2 = 4, je-li A[-1; 4] a u = (1; -1).
- Parametricky vyjádříme přímku p.
p:
x = -1 + t,
y = 4 - t; t ∈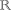
. - Průsečík kružnice a přímky je bod P[x; y], jehož souřadnice splňují jak středovou rovnici kružnice,
tak pro nějakou hodnotu parametru t i parametrické vyjádření přímky p. Do středové rovnice kružnice dosadíme souřadnice x a y
vyjádřené v parametrické rovnici přímky p. Získáme následující kvadratickou rovnici:
(-1 + t - 3)2 + (4 - t - 2)2 = 4. - To můžeme upravit až na
t2 - 6t + 8 = 0 - Podle diskriminantu D této rovnice, rozhodneme jaká je vzájemná poloha dané přímky a kružnice.
Je-li D < 0, rovnice nemá v řešení a přímka p je vnější přímkou kružnice.
Je-li D = 0, rovnice má jedno (dvojnásobné řešení) a přímka p je tečnou kružnice.
Nakonec, je-li D > 0, rovnice má dvě řešení a přímka p je sečnou kružnice. - V našem případě je D = 4 a rovnice má dvě řešení: t1 = 4 a t2 = 2. Tyto dvě hodnoty parametru dosadíme
do parametrické rovnice přímky p a získáme souřadnice bodů P1[3; 0] a P2[1; 2], které jsou hledanými průsečíky.
Určete vzájemnou polohu přímky p: x - y + 5 = 0 a kružnice k: x2 + 2x + y2 - 4y + 1 = 0.
Bodem X0[x0; y0], který leží na kružnici můžeme vést nekonečně mnoho sečen, žádnou vnější přímku a právě jednu tečnu této kružnice. Jak nalézt její rovnici nám řekne následující věta.
Rovnice (x0 - m)(x - m) + (y0 - n)(y - n) = r2, je rovnicí tečny ke kružnici se středem S[m; n] a poloměrem r v bodě X0[x0; y0].
Najděte rovnici tečny kružnice x2 - 2x + y2 - 4y - 20 = 0 v jejím bodě T[4; -2].
- Z předchozí věty víme, jak ze středové rovnice kružnice jednoduše určíme rovnici její tečny v nějakém bodě. Doplníme tedy výrazy x2 - 2x a y2 - 4y na druhé mocniny dvojčlenů x - 1 a y - 2 a určíme její středovou rovnici:
(x - 1)2 + (y - 2)2 = 25. - Rovnice tečny v bodě x[x0; y0] má podle výše uvedené věty tvar:
(x - 1)(x0 - 1) + (y - 2)(y0 - 2) = 25. - Abychom získali rovnici tečny v bodě T, stačí za x0 a y0 dosadit souřadnice bodu T.
(x - 1)(4 - 1) + (y - 2)(-2 - 2) = 25,
3(x - 1) + (-4)(y - 2) = 25,
3x - 3 - 4y + 8 = 25,
3x - 4y - 20 = 0.
Napište rovnici tečny ke kružnici x2 - 6x + y2 - 4y - 5 = 0, která je rovnoběžná s přímkou p: x + y + 4 = 0.
- Rovnice tečny dané kružnice v nějakém jejím bodě X0[x0; y0] má tvar:
(x0 - 3)(x - 3) + (y0 - 2)(y - 2) = 18. - Normálový vektor tečny je n = (x0 - 3; y0 - 2). Víme, že tečna bude rovnoběžná s přímkou p právě tehdy, když její normálový vektor n bude nenulovým násobkem normálového vektoru přímky p. Musí tedy platit:
(x0 - 3; y0 - 2) = k(1; 1), pro nějaké k ∈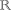\{0} - Z rovnic těchto vektorů můžeme vyjádřit x0 = k + 3 a y0 = k + 2. Protože bod X0[x0; y0] leží na kružnici (je to bod dotyku), musí navíc platit, že
(x0 - 3)2 + (y0 - 2)2 = 18. - Po dosazení za x0 a y0 do této rovnice, získáme kvadratickou rovnici s neznámou k:
(k + 3 - 3)2 + (k + 2 - 2)2 = 18,
k2 + k2 = 18,
2k2 = 18,
k = ± 3. - Pro k = 3 je X0[6; 5], pro k = -3 je X0'[0; -1]. Tečny jsou dvě viz obrázek. To jste ale nejspíše očekávali.
Zjistíme nejdříve rovnici první z nich: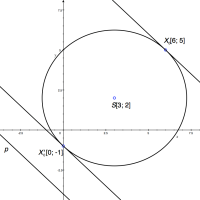
Obr. 5.6: Obrázek k příkladu
3(x - 3) + 3(y - 2) = 18,
3x - 9 + 3y - 6 = 18,
3x + 3y - 33 = 0,
x + y - 11 = 0. - Obdobně získáme i rovnici druhé tečny, která má obecnou rovnici:
x + y + 1 = 0.
Na závěr kapitoly o kružnici si zavedeme ještě jeden pojem, a tím je polára bodu vzhledem ke kružnici. Polára je přímka, která má jednu velice zajímavou vlastnost související s tečnami kružnice.
Přímka daná rovnicí (x - m)(x1 - m) + (y - n)(y1 - n) = r2 se nazývá polára bodu X1[x1; y1] vzhledem ke kružnici se středem S[m; n] a poloměrem r.
Polára bodu X1[x1; y1] vzhledem ke kružnici k se středem S[m; n] a poloměrem r obsahuje body dotyku tečen kružnice k, procházejících bodem X1.
Najděte tečny ke kružnici k: x2 - 2x + y2 + 6y - 6 = 0, které procházejí bodem B[5; 1].
Na následujícím appletu se můžete podívat, jak je polára bodu vzhledem ke kružnici ovlivněna jejich vzájemnou polohou.
