\begin{align} \end{align}

Obecná rovnice přímky

Obecná rovnice přímky je další způsob, jak zapsat přímku v rovině.

Definice

Rovnice
ax + by + c = 0, a, b, c ∈ 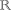realne cislo,
kde alespoň jedno z čísel a, b je nenulové, se nazývá obecná rovnice přímky.

Poznámka

Všechny body X[x; y], jejichž souřadnice splňují nějakou obecnou rovnici přímky, tvoří přímku a naopak každá přímka v rovině je určena nějakou obecnou rovnicí. Obecná rovnice přímky je stejně „silná” jako rovnice parametrická a umožňuje zapsat jakoukoliv přímku v rovině.


Obecná rovnice přímky je určena jednoznačně až na násobek. Rovnice 2x + 3y + 5 = 0 určuje stejnou přímku jako rovnice 4x + 6y + 10 = 0.



Příklad 3.5

Najděte 5 bodů ležících na přímce vyjádřené obecnou rovnicí: 2x - y + 3 = 0.

Řešení
  • Jak určit body ležící na přímce je jednoduché - stačí zvolit jednu jeho souřadnici a z obecné rovnice dopočítat druhou. Zvolme si například hodnotu x-ové souřadnice jako 1. Dosadíme do obecné rovnice přímky a dopočítáme y-ovou souřadnici 2⋅1 - y + 3 = 0,
    y = 5.
  • Na přímce, mimo nalezeného bodu [1; 5], leží například i body: [-2; -1], [-1; 1], [0; 3], [5; 13].

Z obecné rovnice konkrétní přímky snadno zjistíme, které body na ní leží. O něco složitější je to naopak: určit obecnou rovnici přímky, pokud víme, kterými body je určena. Jak nalezneme koeficienty a, b, c obecné rovnice hledané přímky? V parametrickém vyjádření přímky jsme využívali směrový vektor, nyní si zavedeme a použijeme vektor normálový.

Definice

Vektor kolmý ke směrovému vektoru přímky v rovině se nazývá normálový vektor této přímky.

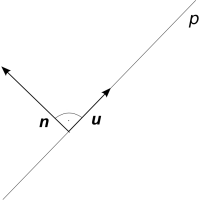
Obr. 3.5: Normálový vektor n přímky p
Obr. 3.5: Normálový vektor n přímky p

Ukážeme si, jak jednoduše ze souřadnic směrového vektoru u získáme souřadnice normálového vektoru n. Označíme si normálový vektor n = (n1, n2), směrový vektor u = (u1, u2). Z definice plyne, že jsou na sebe kolmé, tedy jejich skalární součin je roven nule
n1u1 + n2u2 = 0.

Pokud n1 položíme rovno u2 a n2 rovno - u1 (případně n1 = - u2 a n2 = u1), snadno se přesvědčíme, že uvedená rovnost platí:
n1n2 + n2(-n1) = 0,
n1(-n2) + n2n1 = 0.

To platí pro libovolný vektor u = (u1; u2). Nalezený normálový vektor je n = (u2; -u1) případně n' = (-u2; u1). Při daném směrovém vektoru nám k získání vektoru normálového stačí prohodit souřadnice a u jedné z nich změnit znaménko.

Věta

V obecné rovnici ax + by + c = 0 přímky p(P, u), odpovídají koeficienty a, b souřadnicím jejího normálového vektoru n = (n1; n2); a = n1 a b = n2.

zobraz důkaz
Příklad 3.6

Určete obecnou rovnici přímky p, která je určena body A[3; 1] a B[1; 2].

Řešení
  • Nejprve nalezneme souřadnice směrového vektoru u = AB = (-2; 1). Normálový vektor přímky p je n = (1; 2) a obecná rovnice přímky p vypadá takto:
    x + 2y + c = 0.
  • Zbývá určit koeficient c, ten získáme např. dosazením souřadnic bodu A do získané rovnice. Protože A ∈ p, musí platit:
    3 + 2⋅1 + c = 0, tedy
    c = -5.
  • Obecná rovnice přímky p je:
    x + 2y - 5 = 0.
    Řešení si můžete snadno ověřit dosazením souřadnic bodů A, B do obecné rovnice, ta musí být splněna.
Příklad 3.7
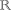  1. Najděte obecnou rovnici přímky q: x = 3 - 2t, y = 2 + t; t ∈ realne cislo.
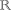  2. Najděte obecnou rovnici přímky q: x = 1, y = 2 + t; t ∈ realne cislo.
  3. Určete parametrickou rovnici přímky q: x - 3y - 4 = 0.
Řešení
  1. Parametrické vyjádření přímky q si můžeme představit jako soustavu dvou rovnic o třech neznámých x, y, t:
    x = 3 - 2t,
    y = 2 + t.
    Budeme se snažit eliminovat parametr t. V našem případě k první rovnici přičteme dvojnásobek rovnice druhé:
    x + 2y = 3 - 2t + 4 + 2t,
    x + 2y = 7,
    x + 2y - 7 = 0.
    Úpravami jsme získali obecnou rovnici přímky q.
  2. V tomto případě nemůžeme použít postup z 1, protože parametru t se nezbavíme. Pokud se zamyslíte, tak uvidíte, že na přímce q leží body [1; 2], pro t = 0, [1; 3] pro t = 1, [1; 4] pro t = 2 atd.
    Z toho plyne, že rovnice přímky q určuje přímku x = 1, což je obecná rovnice přímky q (u přímek rovnoběžných s osou x by se postupovalo obdobně).
  3. K parametrickému vyjádření potřebujeme znát alespoň jeden bod přímky q. Nejprve tedy spočítáme souřadnice nějakého bodu A, který leží na přímce q.
    Zvolíme si jeho x-ovou souřadnici jako x = 1 a dopočítáme souřadnici y-ovou; A[1; -1].
    Teď bychom mohli spočítat souřadnice dalšího bodu, určit směrový vektor a vyjádřit přímku parametricky nebo si uvědomíme, že umíme jednoduše převést normálový vektor na vektor směrový.
    Normálový vektor přímky q, nq = (1; -3) můžeme převést na směrový vektor této přímky uq = (3; 1).
    Pomocí bodu A a vektoru uq vyjádříme parametrickou rovnici přímky q:
    x = 1 + 3t,
    y = -1 + t, t ∈ realne cislo.