Vzájemná poloha přímky a kulové plochy
Vzájemné polohy přímky p a kulové plochy Φ rozeznáváme tři. Navzájem se liší počtem společných bodů. Ty mohou být dva, jeden nebo žádný.
- p ∩ Φ = ∅
Přímka leží mimo kulovou plochu. - p ∩ Φ = {T}
Přímka se kulové plochy dotýká v právě jednom bodě, je její tečnou. Jejich společný bod, bod T, nazýváme bod dotyku. - p ∩ Φ = {X, Y}
Přímka kulovou plochou prochází, jejich společnými body jsou body X a Y.
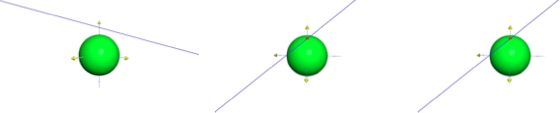
Obr. 6.8: Vzájemná poloha přímky a sféry
Příklad 6.2
Najděte společné body přímky p(P; u) a kulové plochy dané rovnicí x2 + y2 + (z - 2)2 = 4, je-li P[3; 1; 2] a u = (1; 2; -1).
Řešení
- Nejprve si vyjádříme přímku p parametricky.
p:
x = 3 + t,
y = 1 + 2t,
z = -t; t ∈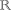 .
. - Vyjádřené souřadnice dosadíme do rovnice sféry a získáme:
(3 + t)2 + (1 + 2t)2 + (-t - 2)2 = 4,
3t2 + 7t + 5 = 0. - Kořeny této kvadratické rovnice odpovídají hodnotám parametru t, určující hledané průsečíky. Diskriminant této rovnice je záporný:
D = 72 - 4⋅3⋅5 = -11.
Rovnice nemá žádné reálné řešení, a proto můžeme říci, že přímka p zadanou sféru neprotíná.
