Protože bodů a směrových vektorů pro vyjádření jedné přímky můžeme zvolit nekonečně mnoho, můžeme jednu přímku vyjádřit nekonečně mnoha parametrickými rovnicemi.
V této kapitole se při zavádění pojmů a řešení úloh přesuneme do prostoru. Úlohy, které budeme řešit, se podobají těm, které jsme řešili v kapitole Geometrie v rovině, a i postupy budou obdobné. Mezi úlohy, které budeme řešit, patří zkoumání vzájemné polohy přímky a roviny nebo třeba výpočet vzdálenosti dvou rovin.
Začneme vyjádřením přímky v prostoru. Přímku v prostoru můžeme vyjádřit jen parametricky, protože obecná rovnice přímky v prostoru neexistuje.
Parametrické vyjádření přímky
Parametrické vyjádření přímky v prostoru zavedeme podobným způsobem jako v rovině.
Úmluva: Přímku p v prostoru, určenou bodem P a vektorem u, budeme zapisovat jako p(P, u).
Jestliže A, B jsou dva různé body, pak vektor u = B - A nazýváme směrový vektor přímky AB.
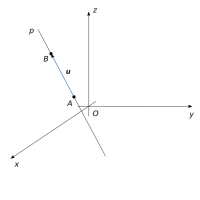
V prostoru zůstávají všechny úvahy i řešení z příkladu 3.1 platné.
Rovnice X = A + tu; t ∈ ![]() , u ≠ o,
, u ≠ o,
se nazývá parametrická rovnice nebo také parametrické vyjádření přímky p(A, u). Proměnná t se nazývá parametr.
Když parametrickou rovnici přímky p(A, u), kde A[a1; a2; a3] a u = (u1; u2; u3) zapíšeme v souřadnicích, získáme vyjádření souřadnic bodů X[x; y; z] této přímky v závislosti na parametru t.
x = a1 + tu1,
y = a2 + tu2,
z = a3 + tu3; t ∈ ![]() .
.
Určete parametrické vyjádření přímky AB, je-li A[2; 3; -1] a B[0; -1; 5].
- Pro určení parametrické rovnice přímky AB použijeme bod A a směrový vektor u = AB:
u = AB = (0 - 2; -1 - 3; 5 + 1) = (-2; -4; 6). - Parametrická rovnice pak vypadá následovně:
x = 2 - 2t,
y = 3 - 4t,
z = -1 + 6t; t ∈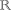 .
.
Zjistěte, zda body A[1; 5; -2], B[2; 3; 0] a C[0; 7; -3] leží na jedné přímce.
- Ze zadaných bodů zvolíme dva, pomocí kterých vyjádříme parametrickou rovnici přímky, která jimi prochází. Do získané rovnice dosadíme souřadnice třetího bodu a hledáme hodnotu parametru t, pro kterou bude parametrická rovnice splněna - pokud taková hodnota existuje, body na přímce leží, pokud ne, body na jedné přímce neleží.
- Z bodů A a B získáme parametrickou rovnici přímky AB:
x = 1 + t,
y = 5 - 2t,
z = -2 + 2t; t ∈ .
. - Za x, y a z dosadíme souřadnice bodu C:
0 = 1 - t,
7 = 5 - 2t,
-3 = -2 + 2t. - Z první rovnice vyjádříme t = -1. Pro t = -1 je splněna i druhá rovnice, ale po dosazení do rovnice třetí vidíme:
-3 = -4.
Soustava nemá řešení, proto bod C neleží na přímce AB. To samozřejmě znamená, že body A, B, C neleží na jedné přímce. - Celý příklad by se dal vyřešit i rychleji způsobem podobným tomu, který jsme použili
v příkladě 3.3.
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor
AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
AB = (1; -2; 2),
AC = (-1; 2; -1).
Ze souřadnic vektorů AB a AC je vidět, že jeden není násobkem druhého, a proto body A, B a C neleží na jedné přímce.
Interval, ve kterém leží parametr t, ovlivňuje stejně jako v rovině, co parametrická rovnice vyjadřuje.
