Funkce exponenciální
V kapitole o kvadratických funkcích jsme se setkali s typem funkcí, kde argument funkce \(x\) byl mocněnec a mocnitelem bylo číslo 2, \(f:y=x^2\). U exponenciálních funkcí je argument jako mocnitel, mocněnec je v tomto případě kladné číslo různé od 1 označované \(a\).
Definice
Exponenciální funkce o základu \(a\) je každá funkce \(f\) na množině \(\mathbb R\) vyjádřená ve tvaru
\(f:y=a^x\),
kde \(a\) je kladné číslo různé od 1.
Poznámka
V případě, že \(a=1\), pak by se nejednalo o exponenciální, ale o konstantní funkci.
V následujícím appletu je možné ověřit vliv základu \(a\) na výsledný graf exponenciální funkce. Budete-li pohybovat posuvníkem, pak uvidíte rovnici dané funkce a zároveň i její graf. Po kliknutí na zoufalého smajlíka se zobrazí, jaký vliv má základ \(a\).
| Vliv základu \(a\) | 
|
Poznámka
Všimněte si, že graf funkce prochází bodem o souřadnicích \([1;a]\), resp. \([-1;\frac{1}{a}]\).
Poznámka
Kdybychom si v průsečíku grafu exponenciální funkce s osou \(y\) představili jeho tečnu pak, podobně jako u kvadratické funkce, se na tuto tečnu můžeme dívat jako na další funkci např. \(g\). Rovnice této funkce je \(g:y=\ln a\cdot x+1\) (kde \(\ln\) je přirozený logaritmus a dozvíme se o něm v následujícím odstavci).
Poznámka
Určité výlučné postavení mezi základy má číslo \(e\) nazývané Eulerovo číslo. Jeho přibližná hodnota je
Exponenciální funkce, jejímž základem je číslo \(e\), se nazývá přirozená exponenciální funkce. Jedinečnou vlastností exponenciální funkce se základem \(e\) je, že rovnice tečny grafu v průsečíku s osou \(y\) je \(g:y=x+1\).
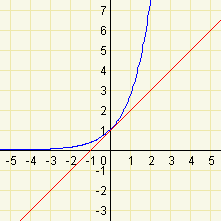
Podle toho, jaká je tečna grafu v průsečíku s osou \(y\) v porovnání s přímkou \(y=x+1\), můžeme odhadnout, jestli základ této exponenciální funkce bude menší, anebo větší než číslo \(e\).
Mohli bychom se také zajímat o to, pro jakou hodnotu základu by tečna měla rovnici \(g:y=-x+1\). Tento základ je převrácená hodnota Eulerova čísla a jeho přibližná hodnota je
\(\frac{1}{e}\ \dot{=}\ 0,367\ 879\ 441\).
