Skládání funkce absolutní hodnota s jinými funkcemi
Jak jsme viděli v první kapitole, můžeme mezi sebou funkce skládat. Podívejme se nyní podrobněji na skládání lineárních, resp. kvadratických funkcí, s funkcí absolutní hodnota.
Skládání lineární funkce a funkce absolutní hodnota
Jestliže je dána funkce \(f:y=ax+b\) a funkce \(y=|x|\), pak složením těchto dvou funkcí můžeme získat dvě různé funkce:
- \(h_1=g\circ f\) \(h_1:y=|ax+b|\)
- \(h_2=f\circ g\) \(h_2:y=a|x|+b\)
Pro konkrétní hodnoty koeficientů \(a\), \(b\) můžeme vykreslit grafy obou funkcí.
1) \(h_1:y=|ax+b|\)
Jak je vidět z appletu, graf funkce, která vznikne složením těchto dvou funkcí v pořadí \(h_1=g\circ f\), můžeme získat tak, že nakreslíme graf funkce \(f\) a část grafu, pro kterou jsou funkční hodnoty záporné, zobrazíme v osové souměrnosti podle osy \(x\). Stejný graf bychom získali i v případě, že bychom vykreslili dvě funkce
\(f_1:y=ax+b\) pro \((ax+b)\geq 0\),
\(f_2:y=-(ax+b)\) pro \((ax+b) < 0\).
Graf funkce \(h_1\) je sjednocením grafů \(f_1\) a \(f_2\).
Poznámka
Výsledný graf si můžeme také prostě představit tak, že část grafu původní lineární funkce, která je pod osou \(x\), 'překlopíme' podél osy \(x\) nahoru.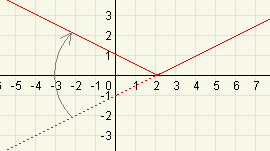
Ukažme si to na konkrétních hodnotách koeficientů \(a\), \(b\).
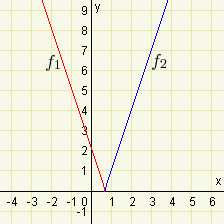
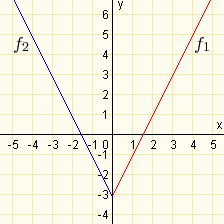
\(f:y=|-3x+2|\)
\(f_1:y=-3x+2\) pro \(-3x+2\geq 0\), tzn. pro \(x\leq {2\over 3}\)
\(f_2:y=-(-3x+2)=3x-2\) pro \(-3x+2 < 0\), tzn. pro \(x > {2\over 3}\)
Poznámka
Pro která \(x\) je výraz uvnitř absolutní hodnoty kladný resp. záporný, můžeme zjistit také tak, že určíme \(x\)-ovou souřadnici \(x_0\) bodu (případně bodů), pro který platí \(f(x_0)=0\). Jinými slovy musíme vyřešit rovnici \(ax_0+b=0\). Tomuto bodu se říká nulový bod. Nulový bod dělí osu \(x\) na dva intervaly \((-\infty;x_0)\) a \((x_ 0;\infty)\). Na každém z těchto intervalů má funkční hodnota stejné znaménko. Vypočteme-li funkční hodnotu pro libovolný argument z těchto intervalů, pak snadno zjistíme, jestli jsou funkční hodnoty v daném intervalu kladné nebo záporné.
2) \(h_2:y=a|x|+b\)
V případě, že skládáme tyto dvě funkce v pořadí \(h_2=f\circ g\), pak graf složené funkce získáme z grafu původní funkce \(f\) tak, že funkční hodnoty pro záporné argumenty získáme zobrazením funkčních hodnot pro kladné argumenty v osové souměrnosti podle osy \(y\). Je vhodné si všimnout, že pro libovolné koeficienty je tato funkce sudá. Ke stejnému výsledku bychom došli i v případě, že bychom vykreslili dvě funkce.
\(f_1:y=ax+b\) pro \(x\geq 0\),
\(f_2:y=-ax+b\) pro \(x\lt 0\).
Graf funkce \(h_2\) je sjednocením grafů \(f_1\) a \(f_2\).
Poznámka
Výsledný graf si můžeme také prostě představit tak, že část grafu původní lineární funkce, která je napravo od osy \(y\), 'překlopíme' podél osy \(y\) doleva.
Ukažme si to na konkrétních hodnotách koeficientů \(a\), \(b\).
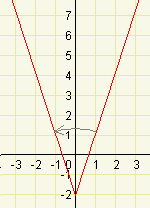
\(f:y=2|x|-3\)
\(f_1:y=2x-3\) pro \(x\geq 0\)
\(f_2:y=-2x-3\) pro \(x\lt0\)
Skládání kvadratické funkce a funkce absolutní hodnota
Jestliže je dána funkce \(f:y=ax^2+bx+c\) a funkce \(g:y=|x|\), pak složením těchto dvou funkcí můžeme získat dvě různé funkce:
- \(h_1=g\circ f\) \(h_1:y=|ax^2+bx+c|\)
- \(h_2=f\circ g\) \(h_2:y=a|x|^2+b|x|+c\)
Pro konkrétní hodnoty koeficientů \(a\), \(b\) a \(c\) můžeme vykreslit grafy obou funkcí.
1) \(h_1:y=|ax^2+bx+c|\)
Jak je vidět z appletu, graf funkce, která vznikne složením těchto dvou funkcí v pořadí \(h_1=g\circ f\), můžeme získat tak, že nakreslíme graf funkce \(f\) a část grafu, pro kterou jsou funkční hodnoty záporné, zobrazíme v osové souměrnosti podle osy \(x\). Ke stejnému výsledku bychom došli i v případě, že bychom vykreslili tři funkce
\(f_1:y=ax^2+bx+c\) pro \(x\in(-\infty;x_1\rangle\),
\(f_2:y=-ax^2-bx-c\) pro \(x\in(x_1;x_2)\),
\(f_3:y=ax^2+bx+c\) pro \(x\in\langle x_2;\infty)\).
Graf funkce \(h_1\) je sjednocením grafů \(f_1\), \(f_2\) a \(f_3\).
Čísla \(x_1\) a \(x_2\) (\(x\)-ové souřadnice nulových bodů) jsou kořeny kvadratické rovnice \(ax^2+bx+c=0\). Tento předpis funkcí \(f_1\), \(f_2\), \(f_3\) je platný pro \(a\gt0\) – rozmyslete si, jaký by měly předpis funkce \(f_1\), \(f_2\), \(f_3\) pro \(a\lt0\).
Intervaly, ve kterých je kvadratický výraz uvnitř absolutní hodnoty kladný, resp. záporný, určíme obdobně jako u skládání funkce absolutní hodnota s lineární funkcí. Nejprve, vyřešením kvadratické rovnice \(ax^2+bx+c=0\) získáme nulové body \(x_1\) a \(x_2\). Tyto body dělí osu \(x\) na tři intervaly \((-\infty;x_1)\), \((x_1;x_2)\) a \((x_2;\infty)\). Na každém z těchto intervalů nemění funkční hodnota své znaménko. Konkrétní znaménko na daném intervalu snadno získáme tak, že spočteme funkční hodnotu v libovolném bodě tohoto intervalu.
Ukažme si to na konkrétních hodnotách koeficientů \(a\), \(b\) a \(c\)
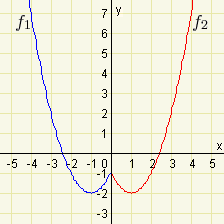
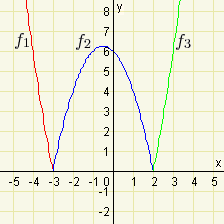
\(f:y=|x^2+x-6|\)
Nulové body této kvadratické funkce jsou \(x_1=-3\) a \(x_2=2\)
\(f_1:y=x^2+x-6\) pro \(x\in(-\infty;-3\rangle\),
\(f_2:y=-x^2-x+6\) pro \(x\in(-3;2)\),
\(f_3:y=x^2+x-6\) pro \(x\in\langle 2;\infty)\).
2) \(h_2:y=a|x|^2+b|x|+c\)
V případě, že skládáme tyto dvě funkce v pořadí \(h_2=f\circ g\), pak graf složené funkce získáme z grafu původní funkce \(f\) tak, že funkční hodnoty pro záporné argumenty získáme zobrazením funkčních hodnot pro kladné argumenty v osové souměrnosti podle osy \(y\). Je vhodné si všimnout, že pro libovolné koeficienty je tato funkce sudá. Ke stejnému výsledku bychom došli i v případě, že bychom vykreslili dvě funkce
\(f_1:y=ax^2+bx+c\) pro \(x\geq0\), \(f_2:y=ax^2-bx+c\) pro \(x\lt0\).
Graf funkce \(h_2\) je sjednocením grafů \(f_1\) a \(f_2\).
Ukažme si to na konkrétních hodnotách koeficientů \(a\), \(b\) a \(c\).
\(f:y=|x|^2-2|x|-1\)
\(f_1:y=x^2-2x-1\) pro \(x\geq 0\),
\(f_2:y=x^2+2x-1\) pro \(x\lt 0\).