Příklady
1. Nakreslete grafy funkcí:
| a) | \(f:y=x^4\) |  |
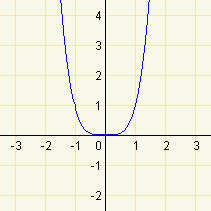
Z výkladu víme, že mocninná funkce s přirozeným - sudým exponentem je sudá. Zároveň víme, že graf této funkce musí procházet body o souřadnicích \([1;1]\) a \([-1;1]\). Pro lepší představu průběhu funkce si můžeme spočítat přibližné souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
-1,4 |
-1 |
-0,6 |
0,6 |
1 |
1,4 |
| \(f(x)\) |
3,8 |
1 |
0,1 |
0,1 |
1 |
3,8 |
| b) | \(f:y=x^7\) |  |
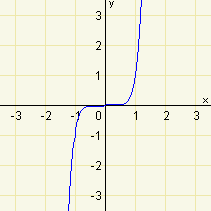
Z výkladu víme, že mocninná funkce s přirozeným - lichým exponentem je lichá. Zároveň víme, že graf této funkce musí procházet body o souřadnicích \([1;1]\) a \([-1;-1]\). Pro lepší představu průběhu funkce si můžeme spočítat přibližné souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
-1,1 |
-1 |
-0,9 |
0,9 |
1 |
1,1 |
| \(f(x)\) |
-1,9 |
-1 |
-0,5 |
0,5 |
1 |
1,9 |
| c) | \(f:y=\sqrt{x}\) |  |
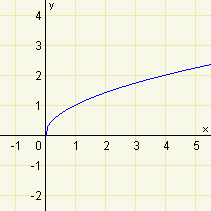
Z výkladu víme, že \(\sqrt{x}=x^{1/2}\). Máme tedy nakreslit graf funkce \(f:y=x^{1/2}\). Definiční obor mocninných funkcí tohoto typu je \(\langle 0;\infty)\), zároveň je to inverzní funkce k funkci \(g:y=x^2\) s omezeným definičním oborem na \(D(g)=\langle 0;\infty)\). Pro lepší představu průběhu funkce si můžeme spočítat přibližné souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
0,5 |
1 |
2 |
4 |
| \(f(x)\) |
0,7 |
1 |
1,4 |
2 |
| d) | \(f:y=\sqrt[7]{x}\) |  |
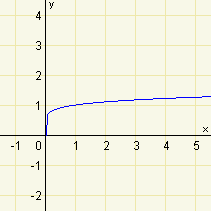
Z výkladu víme, že \(\sqrt[7]{x}=x^{1/7}\). Máme tedy nakreslit graf funkce \(f:y=x^{1/7}\). Dále víme, že definiční obor mocninných funkcí tohoto typu je \(\langle 0;\infty)\), zároveň také, že je to inverzní funkce k funkci \(g:y=x^7\) s omezeným definičním oborem na \(D(g)=\langle 0;\infty)\). Pro lepší představu průběhu funkce si můžeme spočítat přibližné souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
0,5 |
1 |
2 |
5 |
| \(f(x)\) |
0,9 |
1 |
1,1 |
1,3 |
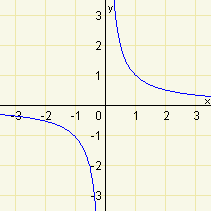
| e) | \(f:y=x^{-1}\) |  |
Z výkladu víme, že mocninná funkce s celým, záporným a lichým exponentem je lichá. Zároveň víme, že graf této funkce musí procházet body o souřadnicích \([1;1]\) a \([-1;-1]\). Pro lepší představu průběhu funkce si můžeme spočítat souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
-2 |
-1 |
-0,5 |
0,5 |
1 |
2 |
| \(f(x)\) |
-0,5 |
1 |
2 |
2 |
1 |
0,5 |
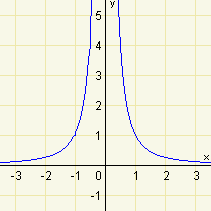
| f) | \(f:y=x^{-2}\) |  |
Z výkladu víme, že mocninná funkce s celým, záporným a sudým exponentem je sudá. Zároveň víme, že graf této funkce musí procházet body o souřadnicích \([1;1]\) a \([-1;1]\). Pro lepší představu průběhu funkce si můžeme spočítat přibližné souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
-2 |
-1 |
-0,71 |
0,71 |
1 |
2 |
| \(f(x)\) |
0,25 |
1 |
2 |
2 |
1 |
0,25 |
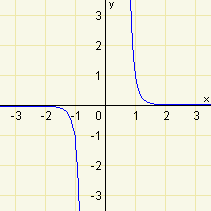
| g) | \(f:y=\frac{1}{x^7}\) |  |
Z výkladu víme, že \(\frac{1}{x^7}=x^{-7}\), máme tedy nakreslit graf funkce \(f:y=x^{-7}\). Mocninná funkce s celým, záporným a lichým exponentem je lichá. Zároveň víme, že graf této funkce musí procházet body o souřadnicích \([1;1]\) a \([-1;-1]\). Pro zvyšující se absolutní hodnotu exponentu se tato mocninná stále více 'přimyká' k ose \(x\). Pro lepší představu průběhu funkce si můžeme spočítat přibližné souřadnice několika bodů, které leží na grafu funkce.
| \(x\) |
-1,2 |
-1 |
-0,9 |
0,9 |
1 |
1,2 |
| \(f(x)\) |
-0,3 |
-1 |
-2,1 |
2,1 |
1 |
0,3 |
2. Rozhodněte, zda jsou následující výroky pravdivé:
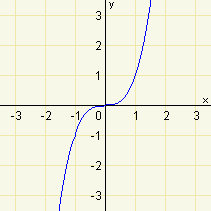
| a) | \((-0,8)^3<(0,2)^3\) |  |
Jedná se o funkční hodnoty funkce \(f:y=x^3\), kde je exponent přirozený lichý. O funkcích s exponentem přirozeným lichým víme, že jsou rostoucí na celém definičním oboru. Pro menší argument nabývá \(f\) menší funkční hodnoty. Výrok je tedy pravdivý.
| b) | \((-1,2)^4<(0,8)^4\) |  |
Jedná se o funkční hodnoty funkce \(f:y=x^4\), kde je exponent přirozený sudý. O funkcích s exponentem přirozeným sudým víme, že jsou sudé. To znamená, že tento výrok můžeme převést na \((1,2)^4<(0,8)^4\). Jak víme, mocninné funkce s přirozeným sudým exponentem jsou na intervalu \(\langle 0;\infty)\) rostoucí. Pro menší argument je menší funkční hodnota. Výrok je tedy
nepravdivý.

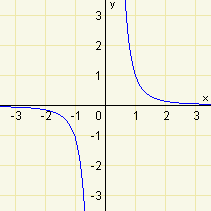
| c) | \((7,2)^{-3}<(3,4)^{-3}\) |  |
Jedná se o funkční hodnoty funkce \(f:y=x^{-3}\), kde je exponent celý, záporný a lichý. Víme, že toto je funkce lichá, klesající na intervalu \((-\infty;0)\) a na intervalu \((0;\infty)\). Oba zadané argumenty jsou z intervalu \((0;\infty)\). Pro větší argument nabývá \(f\) menší funkční hodnoty. Výrok je tedy
pravdivý.
| d) | \((-2,6)^{-6}>(1,7)^{-6}\) |  |
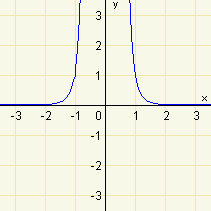
Jedná se o funkční hodnoty funkce \(f:y=x^{-6}\), kde je exponent celý, záporný a sudý. O funkcích s exponentem celým, záporným a sudým víme, že jsou sudé. To znamená, že tento výrok můžeme převést na \((2,6)^{-6}>(1,7)^{-6}\). Jak víme, mocninné funkce s celým, záporným a sudým exponentem jsou na intervalu \((0;\infty)\) klesající. Pro větší argument nabývá \(f\) menší funkční hodnoty. Výrok je tedy
nepravdivý.
| e) | \((0,6)^{1/2}>(0,9)^{1/2}\) |  |
Jedná se o funkční hodnoty funkce \(f:y=x^{1/2}\). O této funkci víme, že je na definičním oboru rostoucí. Pro větší argument nabývá \(f\) větší funkční hodnoty. Výrok je tedy
nepravdivý.

3. V továrně na hračky se vyrábějí ze dřeva (s hustotou \(\varrho=0,6\ \mathrm{g}\cdot \mathrm{cm}^{-3}\)) kostky tvaru krychle.
| a) | Zapište funkci, která vyjadřuje závislost hmotnosti \(m\) kostky na délce \(a\) její hrany. |  |
Nejprve si vyjádříme funkci, která vyjadřuje závislost objemu kostky \(V\) (v \(\mathrm{cm}^3\)) na délce \(a\) (v \(\mathrm{cm}\)) její hrany
\(f:V=a^3\).
Dále si vyjádříme funkci, která vyjadřuje závislost hmotnosti kostky \(m\) (v \(g\)) na objemu dané kostky \(V\) (v \(\mathrm{cm}^3\))
\(g:m=\varrho\cdot V\).
Jestliže složíme funkce \(f\) a \(g\)
\(h=g\circ f\)
dostaneme požadovanou funkci
\(h:m=\varrho\cdot a^3=0,6\cdot a^3\).
Závěr
Funkce, která vyjadřuje závislost hmotnosti \(m\) kostky na délce \(a\) její hrany je
\(h:m=\varrho\cdot a^3=0,6\cdot a^3\).
| b) | Jaká bude hmotnost kostky při délce hrany 4 \(\mathrm{cm}\)? |  |
Zde postačí vypočítat funkční hodnotu pro argument 4 \(\mathrm{cm}\) funkce \(h\) z minulého bodu.
\(h(4)=38,4\)
Závěr
Kostka, jejíž hrana měří 4 \(\mathrm{cm}\), má hmotnost 38,4 \(\mathrm{g}\).
| c) | Kolikrát se zvětší hmotnost kostky, zdvojnásobí-li se délka její hrany? |  |
Zde postačí vyjádřit funkci \(h\) pro délku hrany \(a\) a pro délku hrany \(2a\):
\(h(a)=0,6\cdot a^3\)
\(h(2a)=0,6\cdot(2a)^3=0,6\cdot 8\cdot a^3\)
Odkud je jasně vidět, že hmotnost kostky se zvětší osmkrát.
Závěr
Jestliže zdvojnásobíme hranu kostky, pak se její hmotnost zvětší osmkrát.
4. Zjednodušte dané výrazy:
| a) | \(2^2\cdot2^3\cdot2^4\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(2^2\cdot2^3\cdot2^4=2^{2+3+4}=2^9\)
| b) | \(3^7\cdot3^4\cdot3^5\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(3^7\cdot3^4\cdot3^5=3^{7+4+5}=3^{16}\)
| c) | \(4^2\cdot2^4\cdot8^3\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(4^2\cdot2^4\cdot8^3=(2^2)^2\cdot2^4\cdot(2^3)^3=2^4\cdot2^4\cdot2^9=2^{4+4+9}=2^{17}\)
| d) | \(3^2\cdot9^6\cdot27^5\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(3^2\cdot9^6\cdot27^5=3^2\cdot(3^2)^6\cdot(3^3)^5=3^2\cdot3^{12}\cdot3^{15}=3^{2+12+15}=3^{29}\)
5. Zjednodušte dané výrazy:
| a) | \(x^3\cdot x^2\cdot x\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(x^3\cdot x^2\cdot x=x^{3+2+1}=x^6\)
| b) | \(\sqrt[3]{x}\cdot\sqrt[4]{x}\cdot\sqrt[6]{x}\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(\sqrt[3]{x}\cdot\sqrt[4]{x}\cdot\sqrt[6]{x}=x^{\frac{1}{3}}\cdot x^{\frac{1}{4}}\cdot x^{\frac{1}{6}}=x^{\frac{4}{12}}\cdot x^{\frac{3}{12}}\cdot x^{\frac{2}{12}}=x^{\frac{9}{12}}=x^{\frac{3}{4}}=\sqrt[4]{x^3}\)
| c) | \(x^2\cdot\sqrt{x}\cdot\sqrt[3]{x^2}\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(x^2\cdot\sqrt{x}\cdot\sqrt[3]{x^2}=x^2\cdot x^{\frac{1}{2}}\cdot x^{\frac{2}{3}}=x^{\frac{12}{6}}\cdot x^{\frac{3}{6}}\cdot x^{\frac{4}{6}}=x^{\frac{19}{6}}=\sqrt[6]{x^{19}}\)
| d) | \(\frac{x^2}{x^7}\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(\frac{x^2}{x^7}=x^2\cdot x^{-7}=x^{2-7}=x^{-5}=\frac{1}{x^5}\)
| e) | \(\frac{\sqrt[3]{x}}{\sqrt[9]{x}}\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(\frac{\sqrt[3]{x}}{\sqrt[9]{x}}=x^{\frac{1}{3}}\cdot x^{-\frac{1}{9}}=x^{\left(\frac{3}{9}-\frac{1}{9}\right)}=x^{\frac{2}{9}}=\sqrt[9]{x^2}\)
| f) | \(\frac{\sqrt[5]{x}}{\sqrt[2]{x^9}}\) |  |
Podle pravidel, která byla uvedena ve výkladu, dostaneme postupným upravováním:
\(\frac{\sqrt[5]{x}}{\sqrt[2]{x^9}}=x^{\frac{1}{5}}\cdot x^{-\frac{9}{2}}=x^{\frac{2}{10}-\frac{45}{10}}=x^{-\frac{43}{10}}=\frac{1}{\sqrt[10]{x^{43}}}\)



































