Vliv koeficientů \(k\), \(l\), \(m\) na průběh grafu
Vliv jednotlivých koeficientů si probereme odděleně.
-
Vliv koeficientu \(k\)
Nastavíme-li koeficienty na \(l=0\) a \(m=0\) a koeficient \(k=1\), dostaneme funkci
\(f:y=\frac{1}{x}\).
S touto funkcí jsme se už setkali v předchozí kapitole o mocninných funkcích. Jak je zřejmé, v čitateli nemusí být nutně jen číslo 1, ale libovolné číslo různé od nuly. Takové funkci říkáme nepřímá úměrnost.
Definice
Nepřímá úměrnost je každá funkce \(f\) na množině \(\mathbb R-\{0\}\) vyjádřená ve tvaru
\(f:y=\frac{k}{x}\),
kde \(k\) je reálné číslo různé od nuly.
Pro kladné koeficienty \(k\) je tato funkce klesající na intervalu \((-\infty;0)\) a na intervalu \((0;\infty)\), body grafu funkce jsou pouze v I. a v III. kvadrantu. Pro záporné koeficienty \(k\) je tato funkce rostoucí na intervalu \((-\infty;0)\) a na intervalu \((0;\infty)\), body grafu funkce jsou pouze v II. a v IV. kvadrantu. Dále si můžeme všimnout (zvláště pro hodnoty \(k=1\), \(k=4\), \(k=9\), resp. \(k=-1\), \(k=-4\), \(k=-9\)), že graf funkce prochází body \([\sqrt{k};\sqrt{k}]\) a \([-\sqrt{k};-\sqrt{k}]\) pro kladné hodnoty \(k\) a body \([\sqrt{k};-\sqrt{k}]\) a \([-\sqrt{k};\sqrt{k}]\) pro záporné hodnoty \(k\). Pro snižující se absolutní hodnotu koeficientu \(k\) se graf funkce stále více 'přimyká' k ose \(x\) a k ose \(y\).
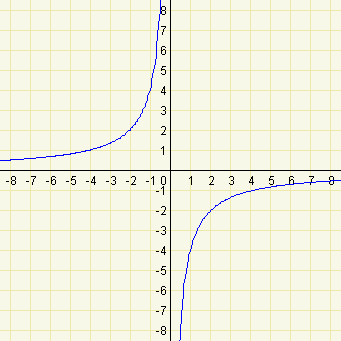
\(k=-4\), \(l=0\), \(m=0\) -
Vliv koeficientu \(l\)
Ponecháme-li koeficienty \(k=1\) a \(m=0\), pak při hodnotě koeficientu \(l=0\) prochází graf funkce bodem \([1;1]\). Při změně koeficientu \(l\) je zřejmé, že se graf funkce 'posouvá' doleva pro kladné hodnoty koeficientu \(l\) a doprava pro záporné hodnoty koeficientu \(l\). Přesněji lze tento 'posun' vyjádřit takto: jestliže graf při koeficientu \(l=0\) procházel bodem \([1;1]\), pak při nenulovém koeficientu \(l\) bude graf procházet bodem o souřadnicích \([1-l;1]\).
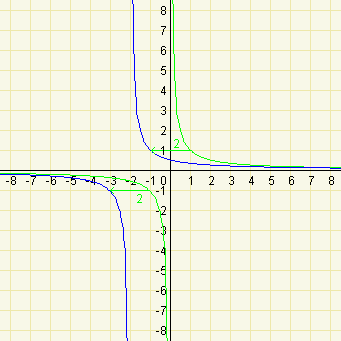
\(k=1\), \(l=2\), \(m=0\) -
Vliv koeficientu \(m\)
Ponecháme-li koeficienty \(k=1\) a \(l=0\), pak při hodnotě koeficientu \(m=0\) prochází graf funkce bodem \([1;1]\). Při změně koeficientu \(m\) je zřejmé, že se graf funkce 'posouvá' nahoru pro kladné hodnoty koeficientu \(m\) a dolů pro záporné hodnoty koeficientu \(m\). Přesněji lze tento 'posun' vyjádřit takto: jestliže graf při koeficientu \(m=0\) procházel bodem \([1;1]\), pak při nenulovém koeficientu \(m\) bude graf procházet bodem o souřadnicích \([1;1+m]\).
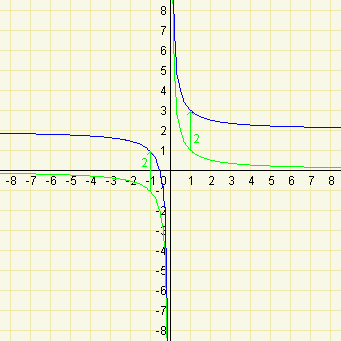
\(k=1\), \(l=0\), \(m=2\)
