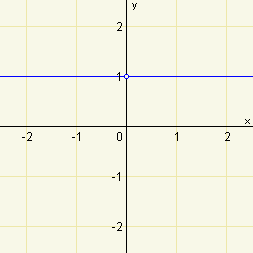
Mocninné funkce s nulovým exponentem
V předchozích odstavcích jsme se snažili vyhnout exponentu \(n=0\). Víme, že libovolné nenulové číslo umocněné na nulu je rovno jedné.
Pro \(x\in\mathbb R-\{0\}\) platí:
\(x^0=1\).
Funkce \(f:y=x^0\) má tedy definiční obor \(D(f)=R-\{0\}\), její funkční hodnota je na celém \(D(f)\) rovna jedné.