Funkce rostoucí, klesající
Funkci nazveme rostoucí tehdy, když s rostoucí hodnotou \(x\) roste hodnota \(y\).
Definice
Funkce \(f\) je rostoucí, právě když pro všechna \(x_1,x_2\in D(f)\) platí: Je-li \(x_1 < x_2\), pak \(f(x_1) < f(x_2)\).Na následujícím obrázku je uveden příklad rostoucí funkce.
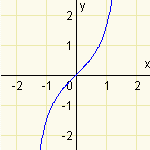
\(y=\mathrm{tg\,}x\)
Funkce je klesající tehdy, když s rostoucí hodnotou \(x\) klesá hodnota \(y\).
Definice
Funkce \(f\) je klesající, právě když pro všechna \(x_1,x_2\in D(f)\) platí: Je-li \(x_1 < x_2\), pak \(f(x_1) > f(x_2)\).
Na následujícím obrázku je uveden příklad klesající funkce.
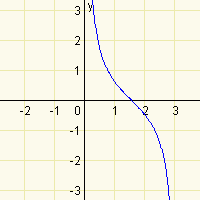
\(y=\mathrm{cotg\,}x\)
Funkci nazveme nerostoucí tehdy, když s rostoucí hodnotou \(x\) klesá nebo se nemění hodnota \(y\).
Definice
Funkce \(f\) je nerostoucí, právě když pro všechna \(x_1,x_2\in D(f)\) platí: Je-li \(x_1 < x_2\), pak \(f(x_1)\geq f(x_2)\).Na následujícím obrázku je uveden příklad nerostoucí funkce.
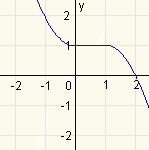
Funkci nazveme neklesající tehdy, když s rostoucí hodnotou \(x\) také roste nebo se nemění hodnota \(y\).
Definice
Funkce \(f\) je neklesající, právě když pro všechna \(x_1,x_2\in D(f)\) platí: Je-li \(x_1 < x_2\), pak \(f(x_1)\leq f(x_2)\).Na následujícím obrázku je uveden příklad neklesající funkce.
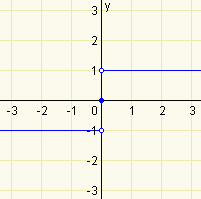
\(y=\mathrm{sgn\,}x\)
Poznámka
Každá rostoucí funkce je zároveň také neklesající funkce. Každá klesající funkce je zároveň také nerostoucí funkce.Funkce rostoucí, klesající na omezeném definičním oboru
Jak víme, ke každé funkci patří její definiční obor. Změnou definičního oboru dostáváme jinou funkci. Máme-li funkci, která není ani rostoucí, ani klesající na svém definičním oboru, můžeme tento definiční obor omezit a tato nová funkce už může být klesající. Je možné také hovořit o tom, že funkce je rostoucí/klesající na určitém intervalu. Ukažme si to na příkladu:
Máme dány dvě funkce
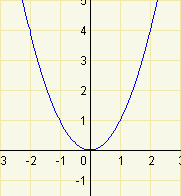 |
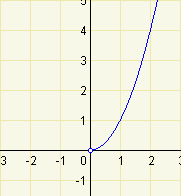 |
| \(f:y=x^2\); \(D(f)=(-\infty;+\infty)\) | \(g:y=x^2\); \(D(g)=(0;+\infty)\) |
Vidíme, že obě funkce mají stejný předpis, ale jiný definiční obor. Funkce \(f\) není ani klesající, ani rostoucí. Funkce \(g\) je na svém definičním oboru rostoucí. Je možné to vyjádřit i tak, že funkce \(f\) je klesající na intervalu \((-\infty;0)\) a rostoucí na intervalu \((0;+\infty)\).
Obdobně je možno definovat nerostoucí/neklesající funkci na omezeném definičním oboru (na intervalu).
